微实验：将结论“做”出来

☉江苏苏州高新区第一中学李莎莉

微实验：将结论“做”出来

☉江苏苏州高新区第一中学李莎莉

在初中阶段的数学教学中，数学实验是学生发现数学结论、找寻化解问题思路的重要途径.因而，培养学生进行数学实验的意识和能力也就成为了数学教学的一项重要内容.在近期的初三年级考前复习中，笔者将一些数学微实验融入解题教学，通过学生手边的一些便捷的工具（如直尺、三角板等）的简单操作，帮助学生获得解题的结果或问题解决的思路，以此提升学生分析和解决问题的能力，取得了较好的教学效果.现将我的做法与各位分享，希望能给您带来启示.

一、两道例题的教学设计及意图分析

例1若P是Rt△ABC的斜边AB上异于A、B的一点，过点P作直线截△ABC，截得的三角形与原△ABC相似，满足这样条件的直线共有（）.

A.1条B.2条C.3条D.4条

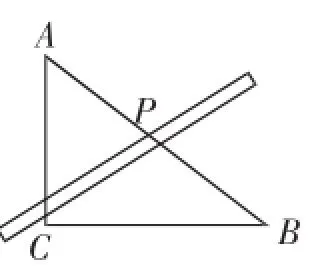
图1

教学设计：请学生作出Rt△ABC，并在其斜边AB取一点P（不与A、B两点重合），如图1.让直尺的一条边过点P，并绕着点P旋转360°，观察旋转过程中直尺的边截△ABC所得的三角形与△ABC是否相似，如果相似，作出这条过点P的直线.请作出所有符合题目要求的直线，并分别标注.

设计意图：通过直尺的简单操作，让学生观察并画出符合要求的直线.在此过程中，直尺的一条边被抽象成一条经过点P的直线，其绕着点P所进行的一周旋转，确保了所有可能出现的符合题意的情形无一遗漏.

例2如图2，已知E、F是⊙O的直径，把∠A为60°的直角三角板ABC的一条直角边BC放在直线EF上，斜边AB与⊙O交于点P，点B与点O重合；将△ABC沿OE方向平移，使得点B与点E重合为止.设∠POF=x°，则x的取值范围是_______.

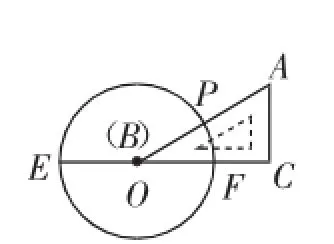
图2

教学设计：取含有60°角的直角三角板，根据题意将其放置到图2中，并按照题目要求进行平移.找出斜边与半圆EF的交点P的位置，观察“三角板沿OE方向平移到点B与点E重合为止”这一过程中∠POF的大小变化情况，确定其“极值”（即最大值和最小值）的位置，并求出x的取值范围.

设计意图：通过三角板的平移操作，学生能体会到∠POF的大小会随着点B的位置的变化发生变化.当点B与点O重合时，∠POF的度数最小；在点B平移过程中，∠POF的度数逐渐增大；当点B与点E重合时，∠POF的度数最大.三角板的操作，将点的移动和角的变化紧密联系在一起，有利于学生确定“极值”位置，获取角的度数的范围.

二、教学感悟

1.过程简述

在呈现例题后，教师先引导学生分析题意，找出身边可以用作探究的工具——直尺和三角板.然后要求学生根据上面的教学设计对例题展开探究，找出符合题意的情形，并给出结论.学生实验结束后，进行了短暂的小组交流，绝大多数学生能将自己探究的历程和探究的结果进行详细阐述.最后安排的是教师引导下的全班交流，两名学生分别将两题的探究历程及正确结果进行了展示，并将自己所积累的实验和解题的经验与大家分享.经统计，通过这两个微实验，近八成学生能给出这两道题的正确答案，在讨论交流中，绝大多数学生说出自己获得结论的过程和数学理由.显然，这两个小的数学实验的效果是显著的.

2.简要评析

两个微型数学实验，工具均来自于学生的文具盒.通过即时、有效的实验探究，学生获得了结论，教师立即引导学生将自己的探究历程及探究结果在小组中展开交流，为的是对过程体验的进一步强化和对结果合理性的进一步“拷问”.在小组交流中，他们所获结果及其获得过程的有效性和合理性将会接受全组同学的“检阅”.最后教师安排基于小组交流之上的全班交流，两名学生不仅展示了结果和过程，还实现了实验经验的分享，这样的交流指向是多维的，成效是明显的.

三、几点思考

微实验，顾名思义就是小实验，就是在数学问题解决过程中能够即时实施的数学实验.基于这样的理解，结合上面的例题教学，我有几点思考与大家分享.

1.数学微实验的工具获取应是便捷的

微实验，要凸显其微小的特点.这些实验一般直接指向的是问题解决，不仅受到空间的限制，还受到时间的限制.所以微实验所需要的材料和工具不能太多，这些较少的材料（工具）应来自于学生身边携带的物品（比如文具等）.以上面的两道例题的求解历程为例，我们所选择的就是直尺和三角板这些学生身边的文具，这些都是学生在探究新知和问题解决中最为常用的工具.对这些工具的应用，学生有着充足的知识与经验铺垫，一方面，他们熟悉这些身边的工具，对直尺和三角板所具有的性质（边、角等方面）了如指掌；另一方面，他们在应用这些工具解决问题的过程中，积累了很多宝贵的经验.事实上，这些工具除了承载知识与经验，还承载着学生已有的丰富的情感体验，在过去的应用中，学生有着充分的成败体验，这些情感的体验，对数学实验的成效影响巨大.显然，数学微实验的工具应来自于学生熟悉的、随身携带的文具用品，它们的加入，将有效唤醒学生已有的知识、经验与情感，激活他们进一步探索的热情.

2.数学微实验的实施情境应是简单的

数学实验，一般都蕴藏在丰富的数学情境中.基于解题的微实验，目标明确，时间短、任务重.所以应有较高的数学化程度.因为过于复杂的问题情境要耗费学生大量的阅读时间和分析时间，对数学实验的生成和实施不利，因此，在教学中，数学微实验的切入，应选择较为简单的问题情境作为实验的载体.本文中介绍的这两则实验，情境都比较简单，所呈现的文本和图形“数学化”程度很高，学生分析并确定实验探究是较为容易的.而学生一旦确定了实验后，简单的文本和图形信息会引领着学生迅速“上手”展开探究，顺利得出结论应该不是难事.综合分析笔者实施的多次数学实验，本文所提的微实验对问题情境的要求是最高的，想要让学生在阅读分析中迅速确定实验的思路和步骤，没有高度的数学化，显然是不行的.为了培养学生实施这类时效性较强的数学微实验的能力，我们应在常态教学中，设计与文中例1、例2类似的数学化程度较高的数学实验，以反复的生成和实施实验，提升学生发现微实验的能力和应用微实验的意识.

3.数学微实验的实施步骤应是简化的

实验，一般都给人以“高大上”的感觉.然而，对于初中数学而言，数学实验在课堂教学中的推广还是近几年的事情.在实施这些数学实验时，我们发现这些与教学同步的实验步骤都较为繁杂，需要教师根据实验的进程进行渐进式引导，用规范的实验语言带领学生展开一步步探索.但是，对于本文所述类似的针对问题解决而生成的即时性数学微实验，笔者认为，不宜有太多的实验步骤，我们在追求便捷工具、简单情境的基础上，还应不断追求简化步骤，力求以最省事的实验路径帮助学生获取数学问题的结果.所以无论是常态数学课堂的微实验教学，还是真正实战中的微实验探索，都应该遵循“步骤简化”的原则设计与实施.看看上面的两个例题，我们就应该清楚“步骤简化”的含义了：例1中，直尺的一边过点P并旋转一周；例2中，将三角板一边与直径重合，拖动顶点B从点O出发，沿着OE平移.在这些简单的操作中，学生依托于实验之上的观察，发现数学化的结论，无论是例1中的作直线，还是例2中的看范围，都是在实验之上的期待生成.正是这样简单易行的操作，让学生的思维得到快速扩张，效果之好，超出想象.

四、结束语

数学微实验是一种简化了的数学实验，不仅实验工具材料少，而且问题情境简单，实验步骤少.这些实验是学生在问题解决中经常出现的，信手拈来，解题效果非常好.然而，如此高效的解题路径，因其非解题的主流路径，而不被一线教师所重视.今天，笔者在这里提出这一概念，并将自己的做法与各位进行简单交流，意在唤醒，唤醒老师们的教学意识，要重视这些微实验，要努力将这些看似简单的解题行为（微实验）通过课堂教学予以规范、强化，并逐步提升为学生在问题解决中的惯性行为.我相信，在大家的不断强化与提升之下，学生的实验意识必然会大幅度提升，其“四基”、“四能”及“三用”也就会得到大幅度的提升或积累.在此过程中，个体数学素养的无形提升是必然的！

以上所述，不当之处，敬请同行专家批评指正！

1.张新尚.“变幻能测”的三角板——解析中考数学试题中的三角板问题［J］.中学数学杂志（初中版），2009（1）.

2.徐凯.三角板中的几何变换问题探究［J］.中学数学（下），2012（3）.

3.郭澄东，卢育新.小小三角板奥妙无穷［J］.中学数学月刊，2007（9）.Z