回归·坚守·创新

☉山东滨州市北镇中学初中部邢成云

回归·坚守·创新

☉山东滨州市北镇中学初中部邢成云

新的课程改革的理念需要落地，需要教学的践行，但若没有中考试题之引领与助推作用，即缺乏最有说服力的评价，行动的落实往往会打折扣.课改理念的召唤及中考试题风向标的合力将有效引领教师转变教学观念，追求更高层级的教学效益.笔者通过对中考试题的研究发现：江西省中考试题（课标卷）较好地落实了课改理念，并不时有创新之举，除了客观评价学生，还关注了学生的可发展性，对思维的深度颇有要求，同时给我们中考研究提供了优质的素材.本文撷取仅用“直尺作图”的一角，探研这类题的立意与价值，期盼更多类似的题目出现，在这类创意作图中彰显数学本味，在限制工具中增大智能挑战性，以发展学力、助力思维、提升数学的综合素养.

笔者发现，从2004年始（课标卷），江西省开始出现仅用“直尺作图”的题目，一开始是立足网格，由明确工具到隐形考查（2005年、2006年），立意清新，到2007年摆脱网格，独出机杼，给人别有洞天之感.2008年-2011年这4年这类题目忽然遁去，但到了2012年回归仅用“直尺作图”，至今连续4年都在此精心策划题目，命制出很有品味的考题.另外，在省命题取向的感召下，省辖大市也纷纷命出此类问题，成为江西省的一道“景观”.以下通过评析的形式与众位同仁共享，以期引起共鸣.

一、借力网格

例1（2004）如图1，已知方格纸中的每个小方格都是相同的正方形.∠AOB画在方格纸上，请在小方格的顶点上标出一个点P，使点P落在∠AOB的平分线上.

分析：很显然，要找到∠AOB的平分线上的一个格点，显然需要这一点到角两边的距离相等，但由于这个点P处于格点位置，靠尺规作图未必能随人愿乖乖地就范于格点.基于此，立足网格、图形及所找点P应满足的条件，直接在图中把它挖出来才是应然之举，需要的作图工具直尺足矣！对∠AOB居于网格的位置进行观察、分析、判断，并用角平分线的概念、判定方法等审视、比对，发现很难直接找到一个格点到角两边的距离相等，这样就督促我们扩大视野、广泛搜索，依托网格线直接（纵横线）或间接（正方形对角线）画出.在此有一个既得经验——角平分线的尺规作图，由于点B、点O处在格点上，根据勾股定理算得BO=5，又OA=5，则有AO=BO=5，此时若再能找到一个格点使它到B、A两点的距离相等（突破了原有到角两边的距离相等这一定势）即可，依托勾股定理及三角形全等等知识，凭借直观与计算发现P1A=P1B=P2A=P2B=、P3A=P3B=5，故图2中的三个点P1、P2、P3均符合题意.（附点P3其他的寻找思路：过点B的横线一定平行于OA，借助“角平分线+平行线=等腰三角形”模型可想到只要将点B沿水平线平移5个单位即可）

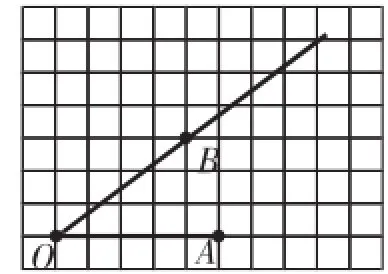
图1

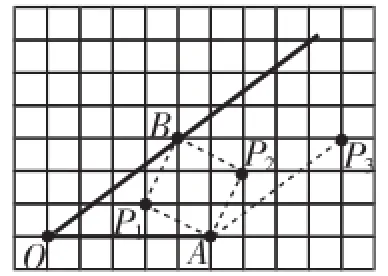
图2

点评：本题把角分线的轴对称性镶嵌于网格内，凸显出只用直尺作图的智能性，在淡化了尺规作图的基础上，深度展现了几何图形的内在属性，以角平分线为核心，联通了勾股定理、三角形全等及等腰三角形等重点知识.

例2（2005）平面直角坐标系中，点A（2，9）、B（2，3）、C（3，2）、D（9，2）在⊙P上.

（1）在图3中清晰标出点P的位置；

（2）点P的坐标是_________.

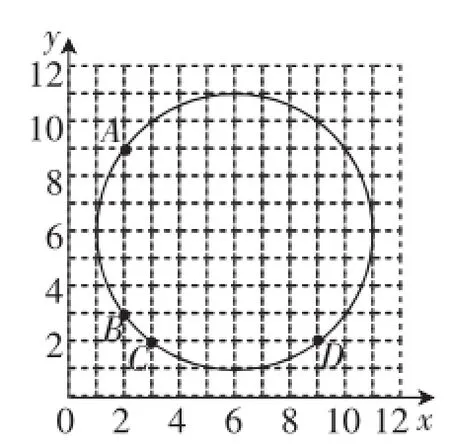
图3

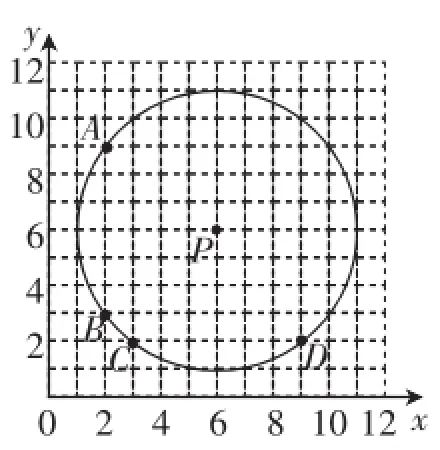
图4

分析：看似没有只用直尺的要求，但隐形考查的就是利用直尺找到交叉点，确立点P的位置，而后写出其坐标.这是因需而用的.答案如图4，即点P（6，6）.

点评：这类题目没有明确让我们作图，但解答的过程中又必须有作图的支持才能化解问题，这种因需而生是活用“四基”的一种折射，它借助网格考查学生的动手操作及思维实验能力.

例3（2006）请在由边长为1的小正三角形组成的虚线网格（图5）中画出一个所有顶点均在格点上，且至少有一条边长为无理数的等腰三角形.

分析：本题看似一个随意性较大的画图，其实关涉两个重要的概念：一是无理数，二是等腰三角形，另外还有格点的限制，是对几何直观的考查.其视角可定位为一边为无理数的、两边为无理数的、三边均为无理数的，如图5中的虚线三角形即为其一（等边三角形）.

点评：本题是一道开放性画图题，它无非是将网格中得天独厚的垂直关系、平行关系挖掘出来，或许就是一个简单的连线，往往给人豁然开朗的感觉，因此这类题备受命题者与考生的青睐.

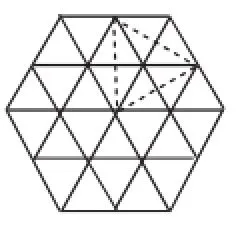
图5

二、无格而作

例4（2007）如图6，已知∠AOB，OA=OB，点E在OB边上，四边形AEBF是矩形.请你只用无刻度的直尺在图中画出∠AOB的平分线（请保留画图痕迹）.

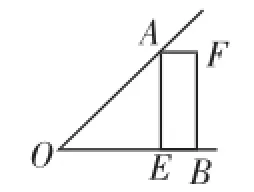
图6

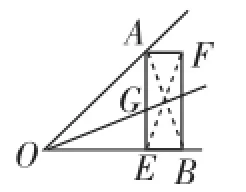
图7

分析：由于已知OA=OB，说明△OAB是等腰三角形.根据“矩形的对角线互相平分”的性质，连接矩形的两条对角线，即可找到AB的中点G.射线OG即是所要作的∠AOB的平分线（如图7）.

点评：本题巧妙地把等腰三角形“三线合一”性质的基本图形与矩形的基本图形进行了有机结合，其妙在于矩形对角线的交点恰为等腰三角形底边的中点，正是这种内在关联，才形成一道别有韵致的好题！

三、梅开二度

例5（2012）如图8，已知正五边形ABCDE，请用无刻度的直尺，准确画出它的一条对称轴（保留画图痕迹）.

分析：本题充分利用了正五边形的性质：5条边相等、5个角相等，是轴对称图形，且有5条对称轴，每一条对称轴都通过顶点，基于这些知识经验的支持，我们只要再找到对称轴上另外一点即可，根据平时研究这个图形积累的经验：若连对角线，等腰梯形、等腰三角形立即显现，依据等腰三角形的对称性，不难想到连接两条对角线即可寻到要找的“点”.即连接BD、CE交于点K，直线AK即为所求（如图9）.这仅是其一，其他4条同法可得.另法：可以固定一个顶点，比如A点，然后分别延长ED、BC交于点O，直线AO即为所求.可见，本题作法不唯一.

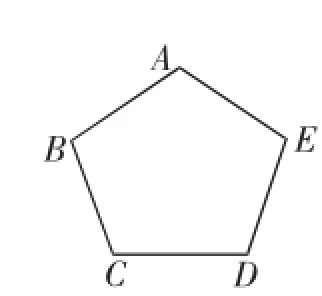
图8

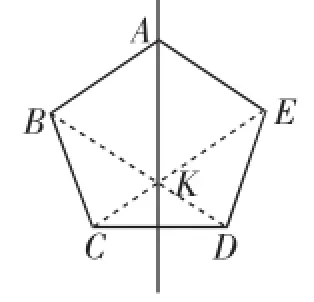
图9

点评：相隔4年，此类题目再次亮相，二度发展，这种回归是对这类题目的进一步创新与坚守.通过本题，我们获得一个发现：正多边形中除了正三角形，其他均可以只用直尺完成对称轴的作图.

例6（2013）如图，AB是半圆的直径，图10中，点C在半圆外；图11中，点C在半圆内，请仅用无刻度的直尺按要求画图.

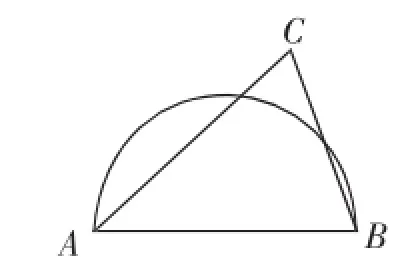
图10

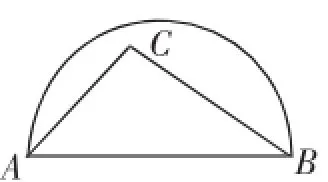
图11

（1）在图10中，画出△ABC的三条高的交点；

（2）在图11中，画出△ABC中AB边上的高.

分析：图10中点C在圆外，要画三角形的高，就是要过点B作AC的垂线，过点A作BC的垂线，但题目限制了作图的工具——无刻度的直尺（只能作直线或连接线段），说明必须用所给图形本身的性质来画图（这就是创新作图的魅力所在），作高就是要构造90°角，显然由圆的直径就应联想到“直径所对的圆周角为90度”.设AC与圆的交点为E，连接BE，就得到AC边上的高BE；同理设BC与圆的交点为D，连接AD，就得到BC边上的高AD，则BE与AD的交点就是△ABC的三条高的交点（如图12）；题（2）是题（1）的拓展、升华，三角形的三条高相交于一点，受题（1）的启发，我们能够作出△ABC的三条高的交点P，再作射线PC与AB交于点D，则CD即为所求（如图13）.

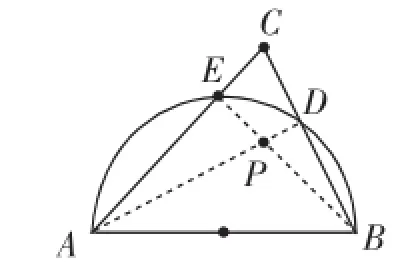
图12

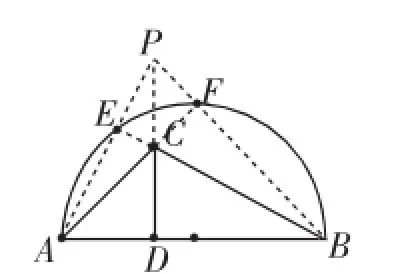
图13

点评：本题是基于一道竞赛题的改造题，归属考查对象的作图创新，它考查考生对圆的性质的理解、读图能力.题（1）要作点，题（2）要作高，都是要解决直角问题，其实用到的知识就是“直径所对的圆周角为直角”.如何灵活调度这一知识实现作图转化是问题的命脉.

例7（2014）已知梯形ABCD，请使用无刻度直尺画图.

（1）在图14中画一个与梯形ABCD面积相等，且以CD为边的三角形；

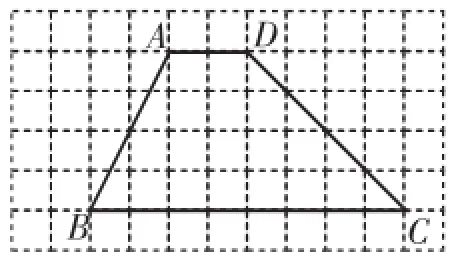
图14

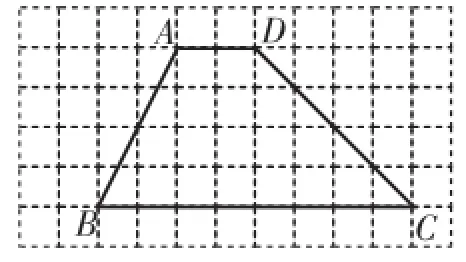
图15

（2）在图15中画一个与梯形ABCD面积相等，且以AB为边的平行四边形.分析：设小正方形的边长为1，则S梯形ABCD=（AD+ BC）×4=×10×4=20.这是问题的出发点，剩下的工作就是如何找到面积值为20的符合条件的图形.

（1）以CD为边，以梯形上下底之和为三角形的底，梯形的高为三角形的高作出△CDE（如图16），或以CD（4）为边作出高为20×2÷4=5的图形（如图17），△CDE就是所作的三角形.

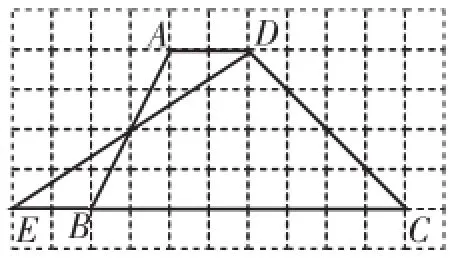
图16

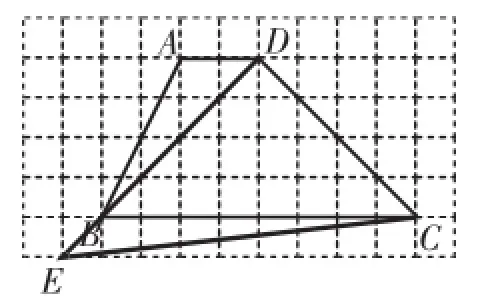
图17

（2）以梯形的高为平行四边形的高，梯形的腰AB为平行四边形的一边，梯形上下底之和的一半为平行四边形的另一边作图.如图18，BE=5，BE边上的高为4，则平行四边形ABEF的面积是5× 4=20，则平行四边形ABEF就是所作的平行四边形.

点评：本题以等积变换为载体，综合考查勾股定理、平行四边形的判定及全等变换等核心知识，同时也揭示了一种图形化归为其他图形常用的方法，是一种化非常规为常规、化不规则为规则的基本思路的展示.

例8（2015）⊙O为△ABC的外接圆，请仅用无刻度的直尺，根据下列条件分别在图19、图20中画出一条弦，使这条弦将△ABC分成面积相等的两部分（保留作图痕迹，不写作法）.

（1）如图19，AC=BC；

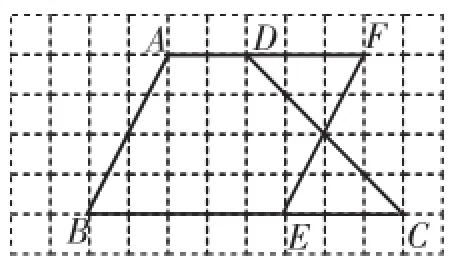
图18

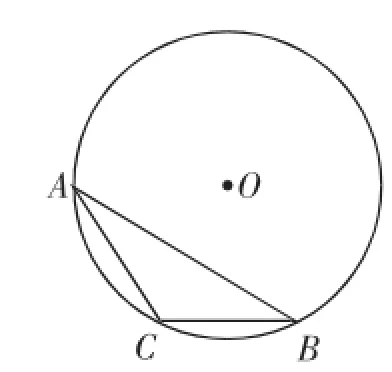
图19

图20

（2）如图20，直线l与⊙O相切于点P，且l∥BC.

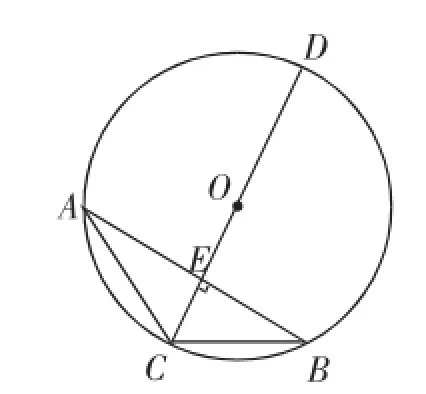
图21

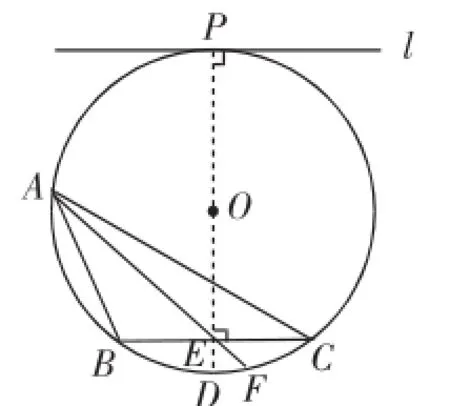
图22

如图22，由l切⊙O于点P，作射线PO，交BC于点E，则PO⊥l.又l∥BC，则PO⊥BC.由垂径定理知点E是BC的中点，连接AE交⊙O于F，则AF为所求作的弦.

点评：本题把等分面积与垂径定理接轨，以“中点”为载体形成交汇，考查的角度比较新颖，第二问增大挑战性，借力切线的性质显现出垂径定理的使用条件，把问题化解，两个问题层级递进，关联密切，形成了一道智趣横生的作图题.

【写在最后】

只用直尺作图，失去了圆规的助力，更多地倾向于考查几何图形的核心本质，其智能性强，其指向具备了常规作图的几何直观和几何性质的思辨等双重功能，原来一般是一些数学爱好者视域内的东西，或者出现在竞赛题中，也就是说这类题型已有先例、并非原创，但在中考中展开考查，并且坚持考查既是一种胆识，也是一种创新，此类淡化尺规作图的题目具有较高的思维价值，是典型的能力立意的好题目，通过作图承载“四基”的考查，新颖别致，活泼灵动，同时为几何教学开辟了一个新路径，我们期待江西省来年的中考仍有“直尺作图”的一席之位.

1.邢成云.只用直尺，所以精彩［J］.中小学数学（初中），2015（9）.

2.钱云祥，钱德春.与初一孩子一起“玩”中考题——一道中考网格题在初一课堂上的尝试与思考［J］.中学数学（下），2015（7）.Z