由“方程组”谈谈数学思维

☉山东淄博市临淄区皇城一中张达

由“方程组”谈谈数学思维

☉山东淄博市临淄区皇城一中张达

数学是思维的体操，数学思维的提升是数学教学的最终目标.方程组思维又是初中学生区别于算术思维需要首先培养的一类思维，如何看待方程组思维及如何培养呢？请看下面的论述.

【案例一】已知x1、x2是方程x2-2x+a=0的两个实数根，且x1+2x2=3-，求x1、x2及a的值.

不怕大家笑话，看着条件x1+2x2=3-，笔者很长时间没有思路，不知怎么处理这个x1加上两个x2.在想了很长时间以后，我才憋出这么个想法来：用上两根之和x1+x2=2，这样不就可以求出x2了吗？！在这样先求出x2，又把x2代回x1+x2=2中求出x1的那一刹那，一种新的想法顿时给我刚刚的欣喜泼了一盆冷水，因为我意识到了一种更为高层次的思维方法——方程组.原来x1+2x2=3-就是关于未知数x1、x2的一个方程、一个条件，它需要连同两根之和这另外一个条件来发挥作用，不可厚此薄彼.

这也解释了为什么盯着x1+2x2=3-没有任何思路的原因，一看到什么条件就想着非从它身上弄出点儿什么结果来，这种直白的、顺序性的思维是不奏效的.

当我有点儿惭愧时，我还要为自己辩护几句：对任何事物的认识都不是一蹴而就的，都得有些原始的、朴素的积累，然后比较、反思，最终形成更高层次的见解.我们切不可踩着这些积累走过来了再回头去说它们基础，说它们“低等”，那样恰恰是不对的，没有这个真实的学习过程，那些所谓的高等认识也是空中楼阁，不接地气，是无根之木、无源之水.

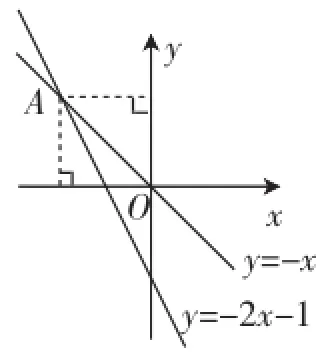
图1

【案例二】“求交点就是联立方程组”这句话说着容易，理解起来不简单.

如图1，求直线y=-2x-1与直线y=-x的交点A的坐标.

同学们多数还是这样做的：列方程-2x-1=-x，其潜在的理解是：题目让求交点的坐标，就是求自变量是多少时两个函数值相等.结果自变量的地位被自然地突出出来了！所以对于用这种一元一次方程的方法解决问题的同学来讲，“方程组”就是不习惯和难以接受的.老师就要去做更细致的点拨：交点的横、纵坐标就是两个未知数，它们的地位是平等的.既然是两个未知数，就需要找两个条件，列两个方程，统筹地解决它们.这两个条件就是交点A同时所在的两条直线，两个方程就是两个解析式.

【案例三】如图2，正方形ABCD的边长为1，点E在边BC上，若∠AEF=90°且EF交正方形外角的平分线CF于点F，在如图3所示的坐标系中，当点E滑动到某处时，点F恰好落在抛物线y= -x2+x+1上，求此时点F的坐标.

我是这样做的：点F在抛物线y=-x2+x+1上，就设点F为（a，-a2+a+1），为了把a求出来，需要再找一个条件.在作了FH⊥x轴之后，再找的条件为FH=CH，这样-a2+a+1= a-1，解得a=，点F为（，-1）.

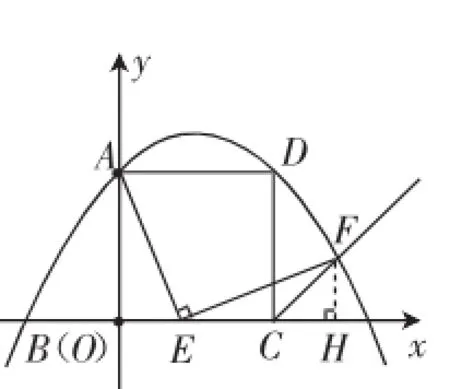
图2

参考答案是这样做的：作FH⊥x轴，设点F的横坐标即BH的长为a，则点F的纵坐标即FH=CH=BH-1=a-1，再把（a，a-1）代入抛物线的解析式得-a2+a+1=a-1，解得a=，点F为（，-1）.

以上两种方法都是有侧重的.

方法1是先利用“在抛物线上”这一条件去设未知数，实际上是想先得到一个结果，即纵坐标可用含横坐标的表达式-a2+a+1表示出来，然后利用“FH=CH”这一条件列方程.

方法2是先利用“FH=CH”这一条件去设未知数，实际上也是想先得到一个结果，即纵坐标可用含横坐标的表达式a-1表示出来，然后利用“在抛物线上”这一条件去列方程.这还是说条件的选择、使用有顺序性，用完一个，再用一个，而不是同时考虑.

要是不分先后，统筹、平等地看待这两个条件（“在抛物线上”“FH=CH”）就会得到方程组：

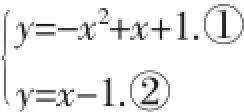
刚才那两种解法就是把①代入②，或把②代入①的问题了.而FH=CH这个条件翻译出来的式子y=x-1就是直线CF的解析式，这个题就是去求抛物线与射线CF的交点.

小结

“方程组”的思维在于整体地、统筹地、平等地对待一个个条件.在翻译出某一个条件时并不指望它能得出一个什么直接的结果，而是耐心地写出另一个后，再综合处理这些方程.学生形成方程（组）思维可以从以下几步去引导.

一是让他们学会代数设想.具体地说，让学生逐步学会在思考问题时，假设问题已经解出，并用某个字母表示，然后去寻求未知量应满足哪些条件，亦即寻求未知量与已知量之间的关系.

二是引导他们学会代数翻译.牛顿这样说过：“要想解一个有关数目的问题或有关量的抽象关系的问题，只要把问题日常语言翻译成代数的语言就成了.”所谓代数语言，基本“词汇”就是代数式，把自然语言翻译成代数语言，就是构造代数式列出方程（组）.

三是引导他们理解解方程（组）的实质.解方程（组）的过程实质上就是通过已知量和未知量的重新组合把未知量转化为已知量的过程.

方程组思维只是众多数学思维中的一种，推而广之，每种思维的培养都可像培养方程组思维这样，深入分析，充分对比，逐步提升，优化认识.这就要求教师在教学中一方面要无条件地相信学生，给予充足的时间和空间，发挥他们的思维潜能，一题多解，集思广益；另一方面要提高点拨的能力，即从一种思维到另一种更高层次的思维的引导、转化、提炼的过程如何更自然和顺理成章.我认为：若我们做好这些，数学思维培养的这一最终目标一定可以实现.Z