重视阅读材料挖掘数学文化——从2016年凉山州中考第24题谈起

☉甘肃礼县职业中等专业学校杨虎

重视阅读材料挖掘数学文化——从2016年凉山州中考第24题谈起

☉甘肃礼县职业中等专业学校杨虎

一、试题呈现

试题：（2016年凉山州高中阶段教育学校招生统一考试数学试题第24题）阅读下列材料并回答问题：

古希腊几何学家海伦（Heron，约公元50年），在数学史上以解决几何测量问题而闻名.他在《度量》一书中，给出了公式①和它的证明，这一公式称为海伦公式.

我国南宋数学家秦九韶（约1202-约1261），曾提出利用三角形的三边求面积的秦九韶公式：

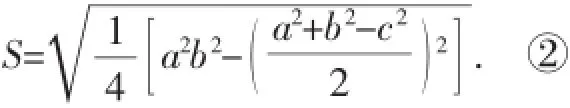
下面我们对公式②进行变形：

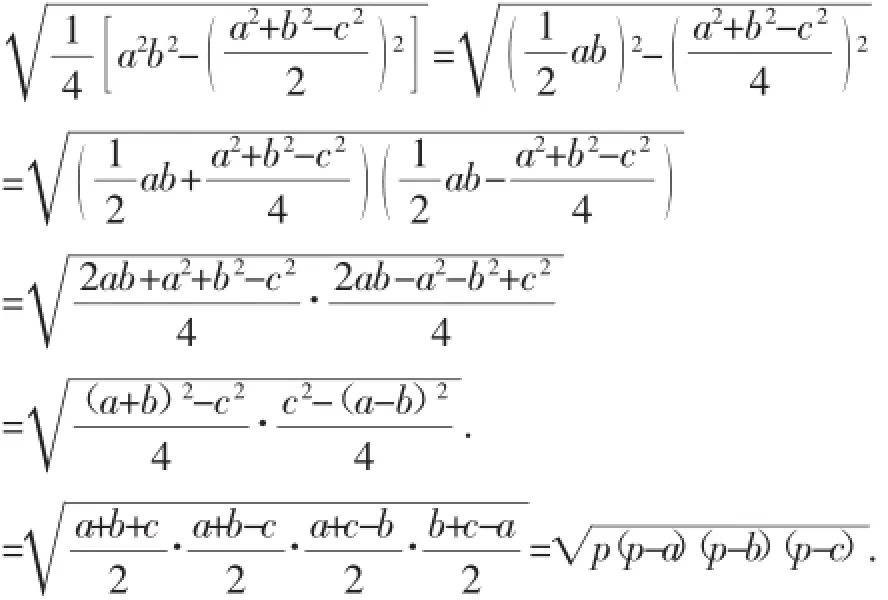
这说明海伦公式与秦九韶公式实质上是同一公式，所以我们也称①为海伦—秦九韶公式.

问题：如图1，在△ABC中，AB= 13，BC=12，AC=7，⊙O内切于△ABC，切点分别是D、E、F.

（1）求△ABC的面积；

（2）求⊙O的半径.

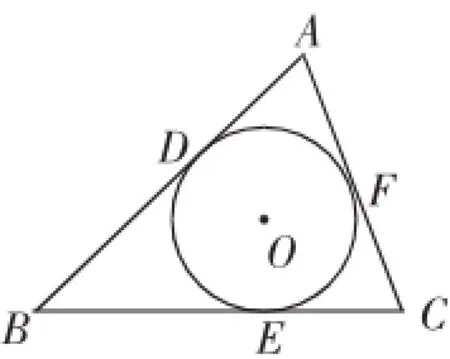
图1

本题是一道材料阅读、分析探究题，取材于人教版义务教育教科书数学八年级（下册）二次根式一章中的阅读与思考，材料题目是海伦—秦九韶公式，与原材料相比试题多了一问，即求三角形内切圆的半径.笔者认为本题选题背景深邃而隽永，文化价值丰富而浓郁，问题解决简约易推广，是一道饱含丰富数学文化的试题.

二、试题解读

1.选题背景深邃而隽永

（1）海伦公式来由.

海伦公式（Heron’s formula或Hero’s formula），又译希罗公式、希伦公式、海龙公式，亦称“海伦-秦九韶公式”.传说是古代的叙拉古（希腊城邦）国王希伦（Heron，也称海龙）二世发现的公式，利用三角形的三条边长来求三角形面积.亦有认为阿基米德已经懂得这个公式，而由于《Metrica》是一部古代数学知识的结集，该公式的发现时期很有可能先于希罗的著作.其基本原理如下所示.

假设在平面内，有一个三角形，边长分别为a、b、c，三角形的面积S可由以下公式求得：

注：“Metrica”（《度量论》）手抄本中用s作为半周长，所以两种写法都是可以的，但多用p作为半周长.

（2）海伦—秦九韶公式来由.

中国宋代的数学家秦九韶也提出了“三斜求积术”，它与海伦公式基本一样.

在我国《九章算术》中，已经有求三角形面积公式“底乘高的一半”，在实际丈量土地面积时，由于土地的面积并不是三角形，要找出它来并非易事.所以他们想到了三角形的三条边.如果这样做求三角形的面积也就方便多了.但是怎样根据三边的长度来求三角形的面积？直到南宋，中国著名的数学家秦九韶提出了“三斜求积术”.

秦九韶把三角形的三条边分别称为小斜、中斜和大斜.“术”即方法.三斜求积术就是用小斜平方加上大斜平方，送到中斜平方，取相减后余数的一半，自乘而得一个数，小斜平方乘以大斜平方，送到上面得到的那个.相减后余数被4除，所得的数作为“实”，作1作为“隅”，开平方后即得面积.

由于任何边的多边形都可以分割成n-2个三角形，所以海伦公式可以用作求多边形面积的公式.比如说测量土地面积时，不用测三角形的高，只需测两点间的距离，就可以方便地导出答案.

所谓“实”“隅”，指的是在一个方程p×2=q中，p为“隅”，q为“实”.于是S、a、b、c分别表示三角形面积、大斜、中斜、小斜（具体推导过程略），所以这一公式也被称为“海伦-秦九韶公式”.

（3）几个优美变式.

以下是这个公式的几个优美变式，其中变式（4）就是秦九韶公式.

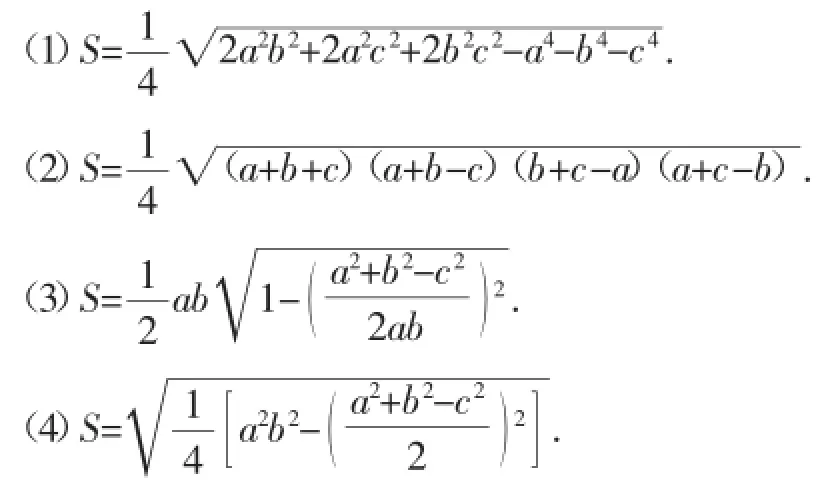
（4）关于公式的证明.

海伦公式的证明方法很多，最基本的思路是在给定的三角形中作内切圆，利用三角形相似来证明.中国古代的数学家梅文鼎在《平三角举要》中，李善兰在《天问或算》中，都给出了证法，其中利用勾股定理进行代数证明比较简单，另外还有向量证法，三角函数证法，利用三角形的面积公式结合余弦定理证明等.限于篇幅，这里不做探究.

由此可以看出，这道试题以课本中的阅读材料为平台，以海伦公式为背景进行命题，不仅因海伦公式结构工整，形式漂亮，让试题充满了视角美，而且也因这个公式吸引好多人探索，让试题具有了背景深邃、内涵隽永的无限韵味.

2.文化价值丰富而浓郁

（1）呼应课标数学文化要求.

数学文化是人类文化的重要组成部分，一直受到数学教育家的普遍关注.这一点在《数学课程标准》中有重要的体现.2001年《数学课程标准（实验稿）》提出：“教材中要注重体现数学的文化价值，在对数学内容的学习过程中，教材可以在适当的地方插入介绍有关数发现与数学史的知识，丰富学生对数学发展的整体认识……”.时隔不久，2011年的《数学课程标准》又重申：“数学文化作为教材的组成部分，应渗透在整套教材中.为此，教材可以适时地介绍有关背景知识，包括数学在自然与社会中的应用，以及数学发展史的有关材料，帮助学生了解人类文明发展中数学的作用，激发学习数学的兴趣，感受数学家治学的严谨，欣赏数学的优美……”.所以这道试题以海伦公式这一数学文化为背景命题是与《数学课程标准》的理念相呼应的.

（2）渗透国内外数学文化.

按照课程标准的建议，人民教育出版社出版的九年义务教育数学教材在阅读与思考或实验与探究栏目设置了一些与“数学文化”有关的内容，让学生在数学学习过程中了解数学与自然及人类社会的联系，进一步了解数学的价值.而本着这一理念，近年来的中考中蕴含丰富数学文化价值的试题颇受各地命题者的青睐，仅2016年这样的试题就有不少，而本题更是以名人（古希腊几何学家海伦）为引子，结合我国南宋时期的数学家秦九韶，给学生展现了优美的海伦-秦九韶公式.从数学史的角度看，世界上的每一个民族都有自己的数学史，而通过自己本国的语言、名人介绍同一个数学问题更能够拉近学生心理上的距离，激发民族自豪感，增强学生对本国数学文化的理解与认同.所以在阅读这道题时就能够带给学生心理上的亲近感和视角上的震撼感，丰富而浓郁的数学文化价值体验也油然而生，因而问题的求解也就自然而清新.

3.问题解决简约易推广

（1）解法.

①第（1）问的解法.

解法1：因a=BC=12，b=AC=7，c=AB=13，则p=16，于是由海伦公式S=

解法2：因为a=BC=12，b=AC=7，c=AB=13，于是由秦九韶公式：得S=

单从运算的角度看，利用海伦公式涉及a、b、c、p四个量，但是计算数值较小，运算量小不易出错；利用秦九韶公式涉及a、b、c三个量，但是运算数字较大，运算量大.

②第（2）问的解法.

解：如图2，连接AO、BO、CO、OD、OE、OF.由于⊙O内切于△ABC，于是OE⊥BC，OD⊥AB，OF⊥AC.设⊙O的半径为r，则OD=OE=OF=r，不难看出S△ABC=S△AOB++S=（r13+12+7）=16r.△AOC

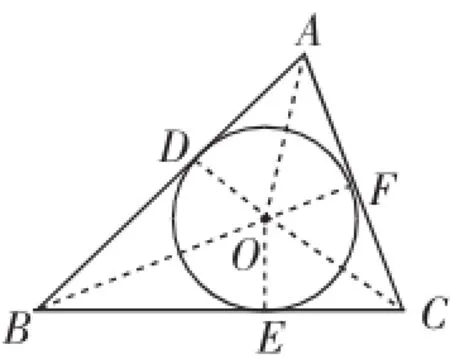
图2

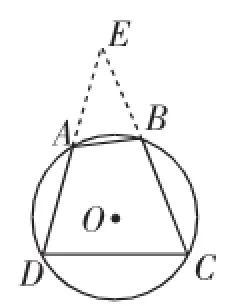
图3

由第（1）问知S△ABC=24，于是16r=24，解得r=，即⊙O的半径为.

（2）推广.

根据试题第（1）问进行如下推广.

推广1：在任意内接于圆的四边形ABCD中，设四条边长分别为a、b、c、d，且则=

由试题第（2）问的求解易得如下推广2.

三、反思与启示

1.反思

从教师的角度分析，阅读材料在教材中没有教学要求，这部分看似“可有可无”的内容在教学中可能被教师一笔带过甚至忽略.因此，在教学中认为只要学生在课余看一看、学一学就可以，抑或持一个无所谓的态度，任由学生“自生自灭”，没有必要引导学生进行探究.这样必然影响到学生对阅读材料学习的态度，认为教师不作要求的内容没有必要学习，因而影响了对阅读材料的学习，忽视了阅读材料中蕴含的重要的数学文化价值.

从学生的角度看，素质教育虽然进行了好多年，数学课程改革也进行得如火如荼，减负的口号也很响亮，然而学生的书包似乎并没有轻多少.大都忙于教师布置的课堂作业、正式作业、课外作业，而很少意识到阅读材料的存在.当然阅读材料有一定的深度与难度，比较抽象，也会让部分学生望而兴叹，失去学习与探索的兴趣.

2.启示

（1）重视阅读材料，提升情感教育.

首先，阅读材料是教学内容的补充和延伸，又是引导学生进行自主探究学习的好素材，充分体现了《数学课程标准》中新的教学理念，可以帮助学生了解数学文化，开拓学习视野，提升发散思维，是教材的重要组成部分.其次，阅读材料丰富了数学课程资源，对教学的弹性预设提供了可能，结合学生的特长个性，有利于教学中因材施教和分层教学的实施.所以对于这部分内容，教师应当鼓励、要求并引导学生去学习，教师重视了，学生的态度也会随之改变；同时也应当借助中考试题的导向作用，将阅读材料渗入课堂，逐步融入教学，汲取阅读材料中的营养，从古今数学发展史，名人故事与名题，数学游戏与趣闻，特别是与我国数学史、数学家有关的题材等入手，让数学教学因为阅读材料而生动有趣，赋予内涵，进一步提高学生的数学学习兴趣，使其理解数学，热爱数学，增强学生的学习热情、爱国热情，真正做到情感教育与考试功能的有机结合.

（2）整合阅读材料，挖掘数学文化.

阅读材料中蕴含的数学文化不仅对揭示数学知识的来源与应用有着重要作用，而且对学生学习数学的积极性与创造性有引导作用.但是阅读材料往往是在章末作为教材的补充以较小的篇幅呈现，缺乏知识的完整性与连续性，这就要求教师广泛阅读各种材料，整合阅读材料，浓缩知识，领会编写意图，创造性地教学，将阅读材料渗透到教学的各个环节；更要挖掘材料背后的数学文化价值，对材料中的定义与概念、公式和与定理、思想及方法进行认真思考和深度融合，并进一步探索如何在教学中将其展现给学生，让学生插上探索的翅膀，尽情翱翔在阅读材料教学的广袤天空中，体验数学文化的博大精深，实现数学文化的育人功能.

1.张安军.数学文化视角下的中考试题赏析及思考［J］.教育实践与研究，2016（6）.

2.张宁.数学文化：情感教育与考试功能有效结合的载体——以“数学文化”为背景的中考试题赏析［J］.中学数学（下），2014（3）.

3.卢多秀.义务教育初中数学课本中阅读材料的教学体会［J］.中学数学教学，1995（4）.

4.人民教育出版社课程教材研究所.义务教育教科书数学八年级（下）［M］.北京：人民教育出版社，2013.

5.梁红京.充分发挥教材中阅读材料的作用［J］.基础教育课程，2008（9）.

6.搜狗百科.海伦公式［E］.http：//baike.sogou.com/ v89877.htm.Z