摭谈“类比推理”在初中数学中的应用

☉江苏省泰州市高港区许庄初级中学王书霞

摭谈“类比推理”在初中数学中的应用

☉江苏省泰州市高港区许庄初级中学王书霞

类比推理是根据两个对象之间的形同和相似进行推理计算的一种重要思想方法，是中学数学解题中的重要方法之一，通过类比推理能够寻求解决问题的思路，可以使模糊的问题清晰化、复杂的问题简单化.初中数学内容广泛，很多内容如代数问题、几何问题、方程问题、函数问题等都需要用到类比推理.本文结合具体案例简要分析了类比推理的实际应用，以达到激活学生思维，提高学习效率的目的.

一、在代数问题中的应用

代数是初中数学的重要内容，是学生学习方程和函数的基础，在中考数学中占有较大比重.在解决代数问题的过程中，教师要积极引导学生巧妙运用类比推理的方法，以帮助学生拨开迷雾，看到问题的实质，从而快速而有效地解决问题.比如，因式分解是初中代数的难点之一，学生对于稍微复杂一点的问题往往会束手无策，如果教师引导学生运用类比推理方法，那么就可以达到事半功倍的效果.

案例1因式分解（x+y-m-n）2-4（x-m）（y-n）.

分析：学生看到题目的第一感觉是难，主要原因是题目比较复杂，学生对于复杂因式分解的题目接触少，以致有一种无从下手的感觉.此时，教师要发挥主导作用，帮助学生分析题目，通过观察变形，学生可以发现题目前后两部分之间联系密切，与以前做过的一道题（a+ b）2-4ab很相似，可以把x-m看成a，把y-n看成b，然后，可以类比这道题的解题过程（a+b）2-4ab=a2+2ab+b2-4ab= a2-2ab+b2=（a-b）2就很容易解决了.

解：（x+y-m-n）2-4（x-m）（y-n）=［（x-m）+（y-n）］2-4（x-m）（y-n）=（x-m）2+2（x-m）（y-n）+（y-n）2-4（xm）（y-n）=（x-m）2-2（x-m）（y-n）+（y-n）2=［（x-m）-（yn）］2=（x-y-m+n）2.

由此可见，在代数解题中，应用类比推理方法可以培养学生的思维能力，大大缩短做题的时间，提高学生做题的效率.

二、在几何问题中的应用

三角形和四边形是初中数学的重要考点，在数学解题过程中，有很多几何问题可通过类比推理的方法去解决，以达到高效快捷的效果.比如，特殊的四边形是中考必考内容之一，也是综合性很强的题目，往往有一定的难度，在解决此类问题时，可以选择类比的方法，往往会取得意想不到的效果.

案例2如图1，四边形ABCD是正方形，E是边BC的中点．∠AEF=90°，且EF交正方形的外角平分线CF于点F，求证：AE=EF．

经过思考，小明展示了一种正确的解题思路：取AB的中点M，连接ME，则AM=EC，易证△AME≌△ECF，所以AE=EF．

（1）如图2，如果把“E是边BC的中点”改为“E是边BC上（除点B，C外）的任意一点”，其他条件不变，那么结论“AE=EF”还成立吗？

（2）如图3，E是BC的延长线上（除点C外）的任意一点，其他条件不变，结论“AE=EF”还成立吗？

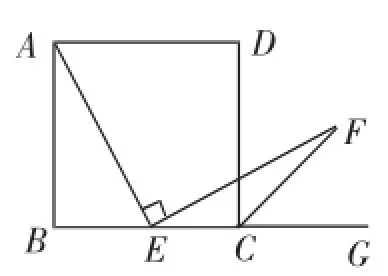
图1

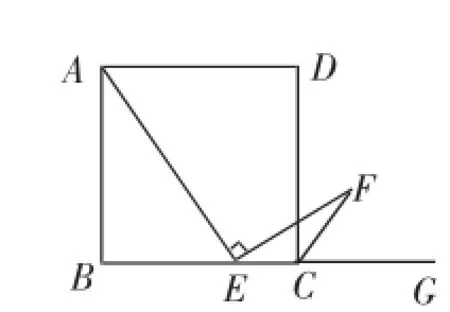
图2

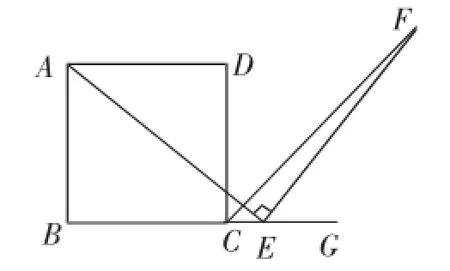
图3

分析：这是一道综合性的中考题，学生对于这种类型的题目往往一看就感觉很难，因此，有的学生甚至连题目没有读完就不看了，实际上如果学生仔细阅读与分析，这道题非常简单，学生只要类比小明的做法就很容易能证明出结论.（2）中可以在AB上取一点M，使AM= EC，即可证明△AME≌△ECF，然后得出结论.（3）中可以在BA的延长线上取一点N，使AN=CE，也易证△ANE≌△ECF，从而得到AE=EF.

解：（1）成立.

证明：在AB上取一点M，使AM=BC，连接ME，如图4.

所以BM=BE.所以∠BME=45°，所以∠AME=135°.

因为CF是外角平分线，所以∠DCF=45°，所以∠ECF=135°.

所以∠AME=∠ECF.

因为∠AEB+∠BAE=90°，∠AEB+∠CEF=90°，所以∠BAE=∠CEF.

所以△AME≌△ECF.所以AE=EF.

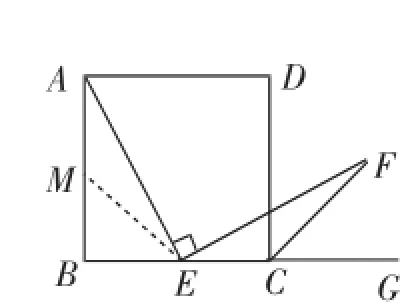
图4

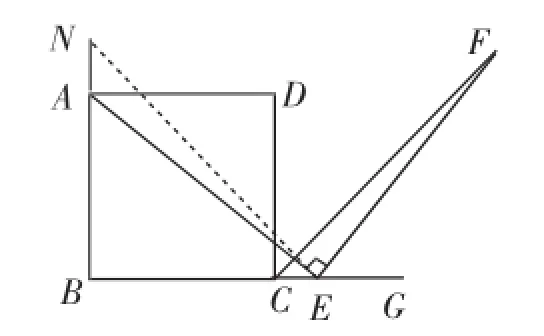
图5

（2）成立.

证明如下：在BA的延长线上取一点N.使AN=CE，连接NE，如图5.所以BN=BE.所以∠N=∠FCE=45°.

因为四边形ABCD是正方形，所以AD∥BE，所以∠DAE=∠BEA.所以∠NAE=∠CEF.所以△ANE≌△ECF，所以AE=EF.

三、在方程问题中的应用

解方程虽然在初中数学中的难度不是特别大，但由于学生学习数学基本遵循由特殊到一般的过程，因此，对于一些带有字母系数的方程，学生解决起来感觉不是很顺利，往往漏洞百出，如果运用类比推理的方法可大大降低出错率，提高做题的速度.

案例3解关于x的方程：ax+b=cx+d（a≠c）.

分析：学生对于含有多个字母的方程往往有一种恐惧感，感觉无从下手，很多情况下直接选择放弃，教师可以指导学生运用类比推理的方法去解决此类问题.可以把这个题目类比方程7x+5=2x-3的解题方法去解决就简单多了.

解：ax+b=cx+d，ax-cx=d-b，（a-c）x=d-b.因为a≠c，所以a-c≠0，所以x=

此题的解题过程主要类比“7x+5=2x-3，7x-2x=-3-5，5x=-8，x=”这一解题过程得到，由此可见，运用类比推理具有较强的优越性.

四、在函数问题中的应用

函数是整个初中数学学习的重点和难点，函数内容在中考数学中占有很大的比重，也是学生失分最严重的题目，究其原因不仅是因为函数抽象性强，难度大，而且与学生不能正确运用合适的解题方法有直接关系.综合性较强的函数题并不孤立存在，往往与其他的知识点有着千丝万缕的联系，学生要仔细观察，认真分析，运用类比的方法往往会大大降低题目的难度，取得正确的解题思路和方法，迅速地得出结果.二次函数是中考的压轴题，难度高、综合性强，在解决此类题目时，可以运用类比推理去解决.

案例4在平面直角坐标系中，抛物线y=ax2+bx+c经过A（-2，-4），O（0，0），B（2，0）三点.

（1）求抛物线y=ax2+bx+c的解析式；

（2）若点M是该抛物线对称轴上的一点，求AM+OM的最小值.

分析：第一问非常简单，把A、O、B三个点代入去解方程组即可得出结果.第二问很多学生感觉很难，主要是不会求最小值的方法，此时，教师可以引导学生类比以前学习求最短距离的问题，通过作对称点，利用两点之间线段最短的道理，连接对称点与另一个点，与对称轴的交点即为所求的点，AB即为最短距离，然后利用勾股定理很容易就求得AM+OM的最小值.

解：（1）把A（-2，-4），O（0，0），B（2，0）三点代入y= ax2+bx+c中，得y=-x2+x.

总之，类比推理是一种有效的数学解题方法，在初中数学中大胆运用类比推理不但可以达到温故而知新的目的，而且可以培养学生的思维能力，使抽象复杂的数学问题简单化，大大提高解题的效率.

1.陆欣芸.类比推理在高中数学教学实践中的应用探讨［J］.学周刊，2016（1）.

2.林桂莲.浅谈类比法在初中数学教学中的应用［J］.教育教学论坛，2013（19）.H