一道考题的思路、难点与教学设计

☉江苏省江阴英桥国际学校吴忠妙

一道考题的思路、难点与教学设计

☉江苏省江阴英桥国际学校吴忠妙

近读《中学数学》（下），不少文章不满足于单纯的解题研究，而是从思路突破到解后反思，再围绕考题给出教学设计，体现了很好的解题研究服务于解题教学的宗旨，笔者深受启发，在研究一道中考试题之后，感觉问题的变式距离偏大，也需要设计系列铺垫来引导学生学会解题，本文就是系列思考之后的梳理，提供研讨.

一、考题思路简述与解后反思

考题（2016年陕西中考卷第25题）（1）如图1，已知△ABC，请画出△ABC关于直线AC对称的三角形.

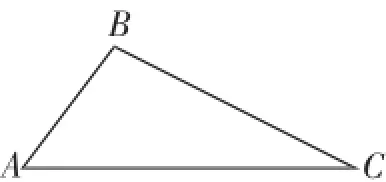
图1

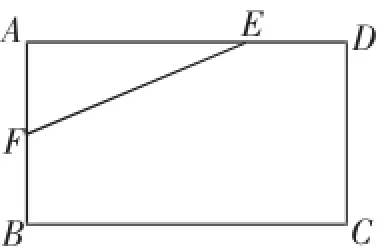
图2

（2）如图2，在矩形ABCD中，AB=4，AD=6，AE=4，AF=2，是否在边BC、CD上分别存在点G、H，使得四边形EFGH的周长最小？若存在，请说明理由.

（3）如图3，有一矩形板材ABCD，AB=3米，AD=6米，现想从板材中裁出一个面积尽可能大的四边形EFGH部件，使∠EFG=90°，EF=FG=米，∠EHG=45°.经研究，只有当点E、F、G分别在边AD、AB、BC上，且AF＜BF，并满足点H在矩形ABCD内部或边上时，才可能裁出符合要求的部件，试问：能否裁出符合要求且面积尽可能大的四边形EFGH部件？若能，求出裁得的四边形EFGH部件的面积；若不能，请说明理由.

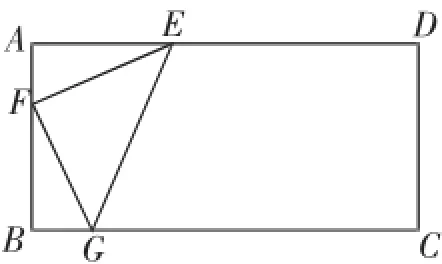
图3

1.思路简述

（1）简单的送分题，只要取点B关于AC的对称点B′，即可画出符合要求的轴对称三角形.

（2）如图4，分别取点E、F关于CD、BC的对称点E′、F′，连接E′F′交BC、CD于G、H两点，则四边形EFGH满足题意.接下来的关于该四边形周长的计算也比较简单，在Rt△AE′F′中思考，求出斜边的长为（2+10）即可.

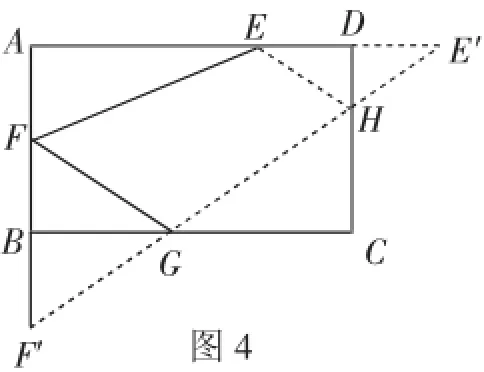
图4

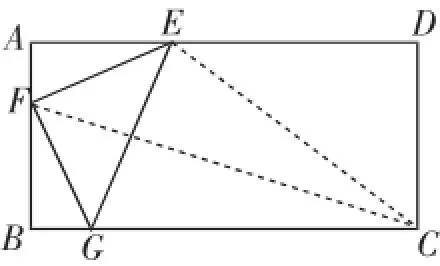
图5

（3）题目条件呈现有些繁杂，需要慢慢梳理、各个击破.比如“EF=FG=，点E、F、G分别在边AD、AB、BC x2+（3-x）2=（）2，解得x=1或2，结合“AF＜BF”知，x=1，即AF=1，BF=2，AF=2，BG=1，即点E、F、G的位置都被唯一确定.

接下来就是分析点H的可能位置了！在分析之前，还有一个准备工作需要明确，这就是当点E、F、G确定之后，如图5，连接CF，则CF垂直平分GE！这可以通过计算CG=CE来证明.这个特殊的位置关系对于进一步分析点H的位置关系十分重要.

图6

现在我们只要结合第（1）问作图的经验，如图6，将△EFG沿GE翻折，得到对称的△F′GE，再以F′为圆心，EF′为半径作圆，设该圆与CF交于点H.如果点H在线段CF上，则该点就是符合要求的一个待求点H.接下来只要设法比较FH与FC的大小，在Rt△BCF中容易求出FC=2，而FF′=，易知F′H上，且AF＜BF”，我们就可确定点E、F、G的位置.如图3，容易根据所谓的“一线三直角”基本图形，证明△AEF≌△BFG，设AF=x，则BF=3-x，则AE=3-x，在Rt△AEF中，是⊙F′的半径，故F′H=，显然FH=+＜ 2，即点H在线段FC上，是符合题意的.此时四边形EFGH的面积也很好求，该四边形的对角线互相垂直，可以用EG·FH求得四边形EFGH的面积为5+m2.

2.解后反思

前面两问都是初中阶段十分常见的教材习题原型考查，第（3）问与前面虽有关联，但是距离较大，要想成功突破，难点有如下几处：

难点之一：E、F、G的位置是否唯一确定？

这是问题突破的起点，如果不能确定E、F、G三点的位置，则后续问题就无从探究.

难点之二：在图5中，FC与EG的特殊位置关系是什么？

如果没有想到FC垂直平分EG，则难有后续构造圆F′与FC的交点生成，而且会陷入“多点共线”的疑问.

难点之三：⊙F′与FC的交点H为什么满足面积最大？

在图6中，根据圆周角定理，矩形内部⊙F′上很多点都满足45°，但为什么⊙F′与FC的交点H是满足要求的，也是由EG与FC的垂直关系带来的.

难点之四：点H是在线段CF上还是在矩形ABCD的外部？

这里的比较涉及计算CF、FH′的长，并比较.关键还是对于正方形的EFGF′的识别和灵活运用.

二、解题教学的微设计

考虑到前两问对第（3）问的启示与关联不大，我们的设计就主要基于第（3）问的几何问题渐次展开.

题目：如图3，矩形ABCD中，AB=3，AD=6，点E、F、G分别在边AD、AB、BC上，∠EFG=90°，且EF=FG=

教学活动1：复习“一线三直角”基本图形

问题1：求EG的长；

问题2：△AEF与△BFG是否全等？对应关系确定吗？

问题3：求AF的长；

问题4：若AF＜BF，求FC的长.

设计意图：通过这组系列问题，让学生熟悉在图3中一些全等的对应关系，并为后续问题的探究做些必要的准备工作.

教学活动2：复习三角形外接圆

在“题目”条件下，增加条件AF＜BF，连接CF.

问题5：请指出CF与EG的位置关系，并说明理由；

问题6：作出△EFG关于直线EG对称的△EGM，并指出四边形EFGM的形状；

问题7：以M点为圆心，ME的长为半径作圆，交直线FC于H点，试判断点H是否在矩形ABCD内部？为什么？

问题8：矩形ABCD边上是否存在点N，使∠EMG= 45°.如果存在，作出符合要求的所有点N；如果不存在，说明理由.

设计意图：通过这一组系列问题，让学生逐个突破上文中提及的几个“障碍点”.

教学活动3：呈现“考题”第（3）问

教学安排：由学生独立思考后，小组内交流讨论，然后大组展示解法思路，教师做好必要的追问，暴露学生对问题的思考.

教学活动4：小结与检测环节

针对学生练习和展示中的解题错漏做必要的小结，并引导学生总结一些常见图形及性质，为快速解题多积累经验.最后安排变式检测题如下：

变式再练：如图7，在矩形ABCD中，AB=3，AD=6，边长为的等腰直角三角形MNG的顶点M、G、N分别在边AD、AB、BC上.

（1）直接写出MN的长；

（2）求BG的长；

（3）当AG＞BG时，连接DG，求DG的长；

（4）在（3）的条件下，求证GD垂直平分MN；

（5）当AG＜BG时，矩形内部（不含边）是否存在点H，满足∠MHN为45°，如果存在，请作图指出点H的位置；如果不存在，说明理由.

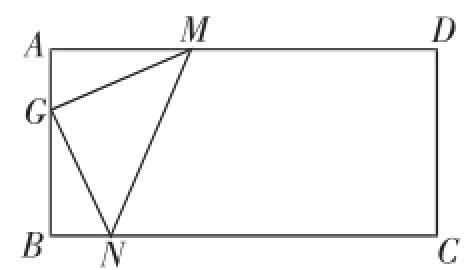
图7

三、有感而发

从近期读刊发现，不论是解题研究、教学研究中的例题设计再到命题研究，都需要教师修炼命题基本功，而这又需要深刻理解初中学段的特征，理解数学的本质，而不是歪解、曲解课标、数学教材上所倡导的教学理念.比如，有些中考题披着重视应用的外衣，设计出晦涩难懂的问题背景，使得问题呈现冗长、题意难懂，不符合“好的数学试题”追求简洁、好懂，体现数学本质的高要求，却被不少命题研究教师贴出诸如“数学来源于生活、服务于生活”“引导重视数学建模”等标签，使得初任教师、广大备考师生无所适从，混淆了对数学的印象.这方面的有益启示，建议同行们多关注北京、上海等地近年来的中考把关题，问题的简约呈现，入口浅宽，深入下去，浓浓的数学味道回味无穷，愿与更多的命题研究者共勉，为命题研究的深入发展而共同努力.

1.中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

2.鲍建生，顾泠沅，等.变式教学研究［J］.数学教学，2003（1，2，3）.H