一道“抽样与数据分析”的中考试题命制历程和反思

☉浙江省台州市白云中学　张安军

一道“抽样与数据分析”的中考试题命制历程和反思

☉浙江省台州市白云中学张安军

《义务教育数学课程标准（2011年版）》对统计部分的内容要求“初中阶段学生通过这部分内容的学习，经历、体验了数据的收集、整理、描述、分析等完整的统计过程，感悟统计思想，学会选择合适的方法收集、整理、分析数据，用数据解决生活情境中与统计有关的问题，建立了数据分析观念，培养了数学应用意识.”［1］这是初中阶段学生必须具备的数学素养，在历届中考中都是必考内容之一.近年来，有关抽样与数据分析的中考解答题的试题虽题型多样，但题型趋于类同，即两张图表（根据已知完整的统计表（图）补全不完整的统计图（表）），一道计算（用样本估计总体比例计算），把抽样与数据分析的统计思想变成简单读图、填空、计算，没有凸显新课标所倡导的统计思想的核心观念.中考试题对当地中学教学、课程改革、学生发展等都会产生了深远的影响.笔者又一次参加2016年浙江省台州市数学中考试题的命制工作，深刻体会到中考试题对当地课堂教学起着重要作用.在这次命制过程中，一道抽样与数据分析的统计试题也经历了曲折的历程，从原有题型的否定、扬弃走向超越.下面谈谈该题的命制过程及自己的感受和反思.

一、命题意图

本试卷共有24道题，本题为第22题，根据命题计划和双向细目表，本题应是一道统计的综合题，难度系数为0.7至0.75，是本试卷的容易题，虽简单容易，但要体现统计的核心思想，即数据的分析观念.数据分析能力应该包含三个方面的内容.首先体会数据蕴含着信息，在以信息和技术为基础的现代社会中，生活中充满了大量的数据，需要人们面对它们作出选择.因此，应该知道数据中蕴含的信息，提高运用其解决问题的意识.其次根据问题的背景选择合适的方法，应意识到统计学的方法只有好与坏之分而没有对与错之分，学生应该学会根据问题选择合适的方法，比如选择抽样的方法，选择合适的统计图表来表示数据、选择合适的数据代表表示数据的波动情况.第三，通过数据分析体验随机性，实际上用来推断总体的样本数据具有随机性，而有足够多的数据就可能从中发现规律，学生通过学习感受到数据具有随机性，但是数据较多时就具有稳定性，这就是统计所特有的思维.

二、命制过程

命题组决定以现实生活为背景，以学生熟悉的事例为载体命制试题，又能很好体现数据的分析观念.于是我们决定在教材中寻找题材，修改一下背景就得到以下的初稿，即一稿.

一稿：为了解某校500名学生的视力情况，该校随机抽取了部分学生进行检查，并将检查结果整理后绘制了如下频数分布表（表1）和频数分布直方图（图1）.

图1　

表1　

请解答下列问题：

（1）为了使样本尽可能具有代表性，下列抽取的样本最合适的是_____.（填写序号）

①某班全体学生的视力情况；

②各班部分男生的视力情况；

③各班学号尾数为6的的视力情况.

（2）根据图表中所给信息，求频数分布表中m的值，并补全频数分布直方图.

（3）视力在哪个范围的学生人数最多？

（4）若视力在4.8以内（不含4.8）为真性近视，请估计该校真性近视的学生人数所占的百分比，并对该校学生的视力情况作出评价.

分析与思考：虽以学生熟悉的生活背景为起点，经历了随机抽样、收集数据、整理数据、描述数据、分析数据及通过数据的分析作出判断，让学生再一次感受统计活动的全过程.但是仔细思考，发现4个设问没有真正涉及统计的核心观念，例如第（1）问在题干中已经随机抽取50名，而第（1）问样本的代表性，是为了考知识点而编题；第（2）问，学生即使没有学习初中这部分内容，根据表中的信息也会求出m的值及补全频数分布直方图，未能让学生从直方图揭示蕴含的信息；第（3）问通过直方图或者表中的信息就能知道哪一组最多，此题考查也是停留在了解，未能考查数据的代表所蕴含的意义；第（4）问是用样本估计总体的思想，但是在平常学生做过太多相类似的练习，即使学生做对，也未必知道此题蕴含的思想，这样一来此题也就成了一道计算题.

命题组还发现，此题缺乏整体性、和谐性，在实际生活中，没有体现出应用统计调查、随机抽样、根据数据进行简单推断的必要性和可能性，套一个背景，改头换面，这也是近年来比较流行的一类统计中考试题，但在考查的本质上没有改变.为了编题而命题，有拼凑之嫌，没有凸显对统计核心的考查.

据上述分析，与课程标准所倡导的数据分析观念相去甚远.命题组决定对此题进行全面调整.

二稿：为了解某校500名学生的视力情况，该校随机抽取了部分学生进行检查，并将检查结果整理后绘制成如图2所示的频数分布直方图（数据包括左端点不包括右端点，精确到0.1）.

表2：保健活动后样本学生视力频数分布表

图2：保健活动前样本学生视力频数分布图

（1）求本次调查所抽取的学生人数.

（2）视力达到4.8及以上为达标，现估计该校的学生视力达标人数大约为188，你认为合理吗？为什么？

（3）为了保护视力，学校开展全校性的视力保健活动.活动结束后，再次从已抽查过的40名学生中随机抽取20名，视力状况结果如表2所示.请选择适当的统计量，从两个不同的角度分析和评价该校开展视力保健活动的效果.

分析与思考：二稿继续以视力为背景，但不同的是本题的立意发生了变化，一稿的题意首先对学校的学生视力状况进行调查，而后进行评价，没有很好凸显统计学学习的价值；二稿在一稿的基础上，首先对全校学生的视力状况进行随机抽查，发现学生在视力方面存在问题，从而提出问题，开展全校性的视力保健活动，为了检测视力保健活动的效果，又进行跟踪调查，从原有随机抽样的40名学生中，再随机抽取20名，再用样本估计总体思想对本次视力保健活动进行评价，让学生经历在实际问题中收集和处理数据、利用数据分析问题、获取信息的过程，体会统计方法的意义，发展数据分析观念，有意识地让学生经历统计活动的全过程.

与一稿相比，二稿更凸显对统计的核心知识的考查.例如，第（1）问从直方图中直接获取信息.第（2）问近年的中考试题都是估计该校视力达标的人数大约为多少，现在从反面思考，即通过样本估计总体得到达标的人数（15÷40）×500≈188，这种估计合理吗？用到统计中的什么思想？第（3）问是一个开放性的问题，有意识地突出统计学的方法只有好与坏之分而没有对与错之分，学生应该根据实际情况选择合适的方法进行解答.对一组数据集中趋势的统计量意义的考查，要求学生深刻理解数据各代表什么意义，并在此能灵活运用，突出调查研究，收集数据，通过分析作出判断，体会数据蕴含着的信息等统计核心观念和思想方法的考查.

不足的是，进行两次抽样，第二次是在第一次人员的基础上进行跟踪调查，这和测量池塘里鱼的条数有类似之处，事实上，第二次可以在500名学生中随机抽取，表2中数据的分布与现实生活相比缺乏科学性，题目的题干上没有交代清楚本次统计活动基于什么目的开展；第四，第（2）问与整个题意不和谐，不自然，是为了考试而人为编题.

三稿：为了保护视力，学校准备开展全校性的视力保健活动，并通过分析活动前后学生的视力情况，评价活动的效果.活动前，随机抽取了部分学生，检查他们的视力，结果如图3（数据包括左端点不包括右端点，精确到0.1）所示.活动后，再次检查这部分学生的视力，结果如表3所示.

图3　：保健活动前样本学生视力频数分布直方图

表3：保健活动后样本学生视力频数分布表

（1）求所调查的学生人数；

（2）视力达到4.8及以上为达标，估计开展视力保健活动前该校学生中视力达标率；

（3）请选择适当的统计量，从两个不同的角度分析活动前后相关数据，评价视力保健活动的效果.

三、感悟

1.注重课标研读，准确定位

每年中考统计试题难度系数低，学生得分高，属于容易题.在一些教师眼里，认为统计试题用不着教，学生都会做；又由于每年的中考统计试题在命制时，命题者未能很好区分第二学段和第三学段的统计知识，导致一些教师在教学认识上存在误区.因此命题组在命制时，准确定位各学段的要求，《标准（2011版）》这部分内容比较如下［2］：

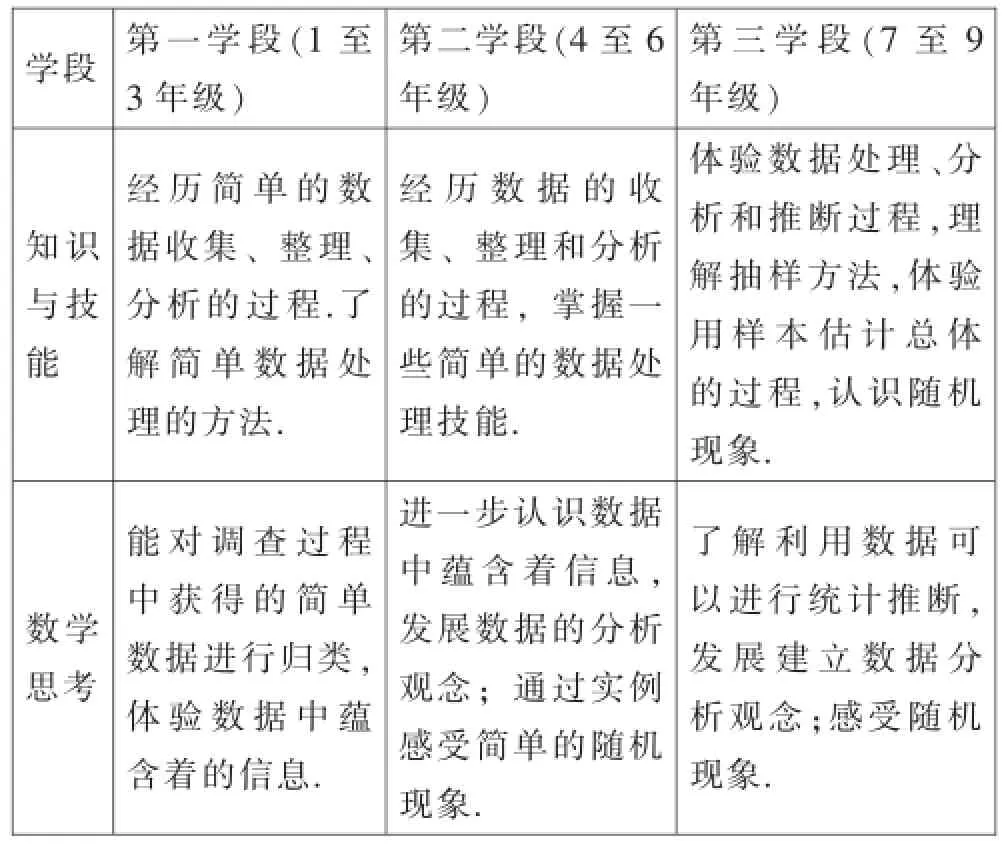
表4　

数据分析可以分为描述性统计分析和推断性统计分析.描述性统计分析是通过集中趋势、离散程度、图形表示等来刻画数据，而推断性统计分析是利用样本的数据去推测总体的情况.由表4知：第一、二学段学生主要学习的是描述性统计分析，第三学段开始接触推断性统计分析.通过对新课标的解读、准确定位，明确考查意图.例如，第（1）问注重直方图数据信息的获得，第（2）问注重数据的分析，第（3）注重数据的预测与推断，重在推断性统计分析和考查.

2.重视统计的应用价值，突出核心观念的考查

试题以学生视力问题为背景，设置前测与后测，第一次视力检测，发现学生视力存在问题，第二次检测是对视力保健活动的效果进行评价，评价的结论开放，让学生意识到统计学的方法只有好与坏之分而没有对与错之分，学生能根据实际问题选择合适的方法.例如对于本试题，可用平均数、众数等对这次活动作出简单的判断.对活动的评价，实际上需要学生对平均数、众数、中位数等统计量有深刻的理解和辨别，同时要对各统计量之间的关系有非常清楚的认识，注重对统计意义的深层考查.试题同时重视统计过程的完整性，通过具体情境的创设，让学生对抽样方式、样本的代表性等进行考查，渗透样本估计总体的思想，突出数据分析的考查.

1.陈莉红，等.2014年中考数学试题“抽样与数据分析”分类解析［J］.中国数学教育，2015（1-2）.

2.中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学教育出版社，2012.Z