“外 心” 真 会 玩

江苏省海门中学　(226100)

何振华



“外心”真会玩

江苏省海门中学(226100)

何振华

在各类模拟考试中，经常出现与外心有关的考题，很多学生遇到这类考题往往不能找到问题的切入点，感到无从下手，本文意欲与大伙一起突破思维障碍，玩转“外心”.

下面以2015泰州模考的填空题14题为例，谈谈如何发现外心问题的切入点.

在ΔABC中，D为边AC上一点，AB=AD=4,AC=6,若ΔABC的外心恰在线段BD上，则BC=.

分析：在ΔABC中，已知AB=AD=4,AC=6，只需求出∠BAC，即可用余弦定理求出BC，因此本题的思维障碍在于怎么求∠BAC，那么如何运用条件“ΔABC的外心恰在线段BD上”就显得十分重要.

思维突破角度一：外心联想到外接圆，再联想到圆的几何特征：圆心角等于圆周角的2倍.

图1

思维突破角度二：外心联想到外接圆，再联想到圆的方程，构建方程组，求出∠BAC的余弦值.

图2

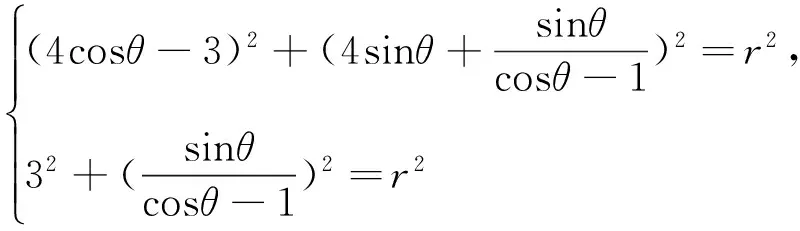
评注：利用圆方程求解，可以将几何问题代数化，往往可以降低问题的思维难度，可以更快的找到问题的切入点，需要具备这种思维意识.

思维突破角度三:由外心联想到外心是中垂线的交点，构建三角形，利用三角形相似，求出∠BAC的余弦.

图3

评注：外心是中垂线的交点这一特征可以帮助我们确定外心位置，因此也是处理外心问题的常规手段.

图4

则λ的值为.都可使用性质处理.

总的来说，如果你能从外心的特征出发，结合解析几何、平面几何和解三角形和向量知识，那么就一定能突破外心问题的思维障碍，找到外心问题的切入点，玩转“外心”.