一道省质检试题的探究与推广

福建省泉州市第七中学　(362000)

杨建益　黄永生



一道省质检试题的探究与推广

福建省泉州市第七中学(362000)

杨建益黄永生

1　问题呈现

(2016年福建省质检文科数学20题)已知点

A(-4,0),直线l:x=-1与x轴交于点B,设动点M到A,B两点的距离之比为2.

(Ⅰ)求点M的轨迹C的方程；

(Ⅱ)设C与x轴交于E,F两点，P是直线l上一点，且点P不在C上，直线PE,PF分别与C交于另一点S,T，证明：A,S,T三点共线.

2　问题分析与解答

试题考查圆的方程、直线与圆的位置关系等基础知识，直接利用已知条件中的等量关系，将其代数化，并化简，便可解决(Ⅰ).本题(Ⅱ)中，证明三点共线问题，可以转化为两点的斜率相等加以解决.

图1

解:(Ⅰ)x2+y2=4.过程略.

(Ⅱ)由(Ⅰ)知曲线C的方程为x2+y2=4，如图1，令y=0得x=±2，不妨设

E(-2,0),F(2,0)．设

P(-1,y0),S(x1,y1),T(x2,y2)，则直线PE的方程为y=y0(x+2)，由

评析:解析几何的核心问题是用代数的方法来解决几何问题.本题的几何关系为“A,S,T三点共线”,代数化为“kAS=kAT”.由于A为定点，因此本题的第(Ⅱ)问可重新表述为：“设C与x轴交于E,F两点，P是直线l上一点，且点P不在C上，直线PE,PF分别与C交于另一点S,T，证明：直线ST过定点A.”

3　问题思考

根据命题的重新表述，注意到直线l:x=-1与A(-4,0)的特殊性，引发下列思考：

(1)直线l:x=n(n≠0)，则满足题目条件的点A的坐标是什么？

(2)该命题的逆命题是否成立？

(3)其他的曲线(椭圆、双曲线、抛物线)是否有相应的命题成立？

4　问题探究

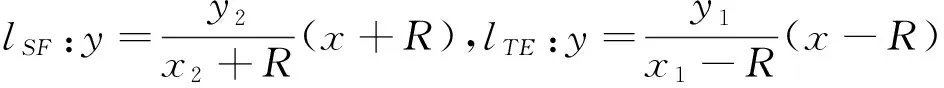
将(1)代入(2)，化简得

所以，点P的轨迹为定直线x=n.

对于椭圆、双曲线、抛物线也有相似的如下结论：

结论5已知抛物线C:y2=2px的顶点为O，P是直线l:x=n(n≠0)上一点，且点P不在C上，直线PO与C交于点S，过点P作与x轴平行的直线交C于点T，则直线ST过点A(-n,0).

上面三个结论的证明与结论1证明类似，这里提供结论3的一种简证方法.

通过进一步探究，以上三个结论的逆命题也成立，即:

结论8已知抛物线C:y2=2px的顶点为O，过A(-n,0)(n≠0)的直线与抛物线C交于S,T两点，过点T作与x轴平行的直线与直线SO的交点为点P,则点P的轨迹为定直线x=n.

限于篇幅，结论6,7,8证明从略.

[1]黄永生,杨丹.2015年高考福建文科数学卷第19题(Ⅱ)的探究与推广[J].福建中学数学，2016(2):11-12.