猜 想·论 证——一类圆锥曲线问题的处理与分析

江西省九江第一中学　(332000)

杨艳萍



猜想·论证
——一类圆锥曲线问题的处理与分析

江西省九江第一中学(332000)

杨艳萍

圆锥曲线中求范围、定点、定值的问题，由于其难度大、计算复杂等特征，一直是高中生学习的一个难点.很多时候学生有想法，能够设计出有效解题方案，但在繁杂的计算过程中却因笔误、计算失误等原因导致丢分严重.如果通过对题目条件的解读，能够利用特例或运动极限观快速猜测出答案，则为构建解题思路和解题技巧提供了方向，还可以及时发现并纠正计算过程中的种种失误、有效减少出错，从而提高解题的准确率.

1.用特例或运动极限观解答圆锥曲线中求范围、定点、定值问题的基本思路

(1)利用特例解答圆锥曲线中求范围、定点、定值问题

基本思路：特例⟹猜测结果⟹检验结果⟹得出结论;

(2)利用运动极限观解答圆锥曲线定点、定值问题

基本思路：极限位置⟹猜测定点(值)⟹检验定点(值)⟹得出结论.

2.用特例或运动极限观解答圆锥曲线中求范围、定点、定值问题的优点

(1)由特例或极限位置能够快速猜测到结果，提高学生解答本题的自信心；

(2)检验结果时，发现与猜测结果不吻合，可以立刻重新计算或重新思考，有效杜绝因笔误、计算失误而导致的丢分，从而提高准确率.

一、利用特例解答圆锥曲线定点、定值问题

例1(2016高考全国卷)设圆x2+y2+2x-15=0的圆心为A，直线l过点B(1,0)且与x轴不重合，l交圆A于C，D两点，过B作AC的平行线交AD于点E.

(1)证明|EA|+|EB|为定值，并写出点E的轨迹方程；

(2)设点E的轨迹为曲线C1，直线l交C1于M,N两点，过B且与l垂直的直线与圆A交于P,Q两点，求四边形MPNQ面积的取值范围.

图1

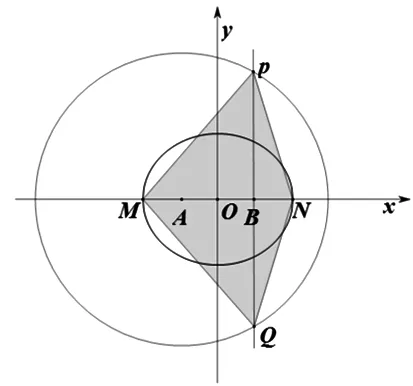
图2

(取特例)②，如图2，直线l与x轴重合;易得|MN|=2a=4，|PQ|=

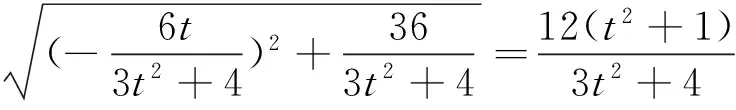
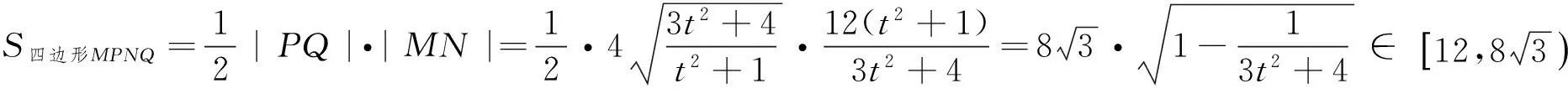
图3

(1)求椭圆E的方程；

(2)(分析)常规方法解答此题，学生无从下手，很茫然，不知道怎样将P，Q两点关系转化为代数式；如果取直线l的特例，猜测出点Q的坐标，将抽象的点Q转化为具体的点Q再进行证明，学生就有一种拨开云雾见青天的感觉.

(取特例)①当直线l与x轴平行时，设直线l与椭圆相交于A、B两点.

(猜测定点)所以，若存在不同于点P的定点Q满足条件，则Q点的坐标只可能为Q(0,2).

图4

(检验定点)下面证明：

当直线l的斜率不存在时，由特例可知，结论成立.

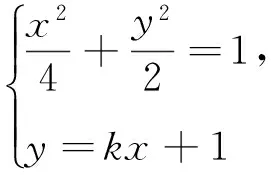
(1)求椭圆C的方程；

(2)点P是椭圆C上除长轴端点外的任一点，连接PF1，PF2.设∠F1PF2的角平分线PM交C的长轴于点M(m,0)，求m的取值范围；

图5

图6

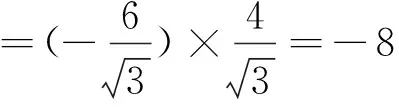
二、利用运动极限观解答圆锥曲线定点、定值问题

图7

例5已知△ABC的两个顶点A,B的坐标分别是(0,-1),(0,1)，且AC,BC所在直线的斜率之积等于m(m≠0)．

(1)求顶点C的轨迹E的方程，并判断轨迹E为何种圆锥曲线；

-mx2+y2=1(m≠0).

当m<-1时,轨迹E表示焦点在y轴上的椭圆，且除去(0,1),(0,-1)两点；

当m=-1时,轨迹E表示以(0,0)为圆心半径是1的圆，且除去(0,1),(0,-1)两点；

当-1

当m>0时,轨迹E表示焦点在y轴上的双曲线，且除去(0,1),(0,-1)两点.

图8

(猜测定点)直线MQ与x轴的交点为定点(2,0).

图9

(得出结论)直线MQ过定点(2,0).