用“无穷远点”探究圆锥曲线的一个统一性质

江苏省南京市六合区程桥高级中学　(211504)

竺宝林



用“无穷远点”探究圆锥曲线的一个统一性质

江苏省南京市六合区程桥高级中学(211504)

竺宝林

性质1从椭圆一个焦点发出的光，经过椭圆反射后，反射光线都汇聚到椭圆的另一个焦点上(如图1)；

性质2双曲线的光学性质：从双曲线一个焦点发出的光，经过双曲线反射后，反射光线的反向延长线都汇聚到双曲线的另一个焦点上(如图2)；

性质3抛物线的光学性质：从抛物线的焦点发出的光，经过抛物线反射后，反射光线都平行于抛物线的轴(如图3).

图1 图2 图3

上述椭圆、双曲线、抛物线的性质称为圆锥曲线的光学性质，其实质是圆锥曲线的切线的一个统一性质.

圆锥曲线的统一性除了教材中的统一定义外，利用极限思想，还可以表述为：椭圆的一个焦点F1在平面的有限位置，另一个焦点F2向右平移到无穷远点，椭圆在无限远处闭合，在平面有限位置的可见部分变成了抛物线；当F2绕过无穷远点又回到平面的有限位置，但F1,F2左右位置关系反转了，此时曲线在平面有限位置的可见部分变成了双曲线的左右两支.

为了使双曲线、抛物线与椭圆的光学性质在表述上统一，文[1]提出了“无穷远处”和“无穷远点”的概念：当直线与x轴相交时，其交点为x轴上一确定的点，当直线与x轴平行时，其交点在x轴的无穷远处.具体对于双曲线而言，我们可以认为，经过焦点F1的光线，被双曲线反射后，经无穷远处后回到了焦点F2；对于抛物线而言，焦点发出的光源经抛物线反射后，反射光线平行于抛物线的对称轴，经过抛物线的无穷远处的顶点或焦点.

依照上述说法，圆锥曲线的光学性质可以统一表述为：

定理1从圆锥曲线一个焦点发出的光，经过该曲线反射后，反射光线都汇聚到该曲线的另一个焦点上.

笔者在研究圆锥曲线的性质时，还得到抛物线的另一个性质：

图4

性质4如图4，点P(x0,y0)为抛物线y2=2px(p>0)上任意一点，P点处的切线分别交y轴于点T，过点P作PB∥x轴，交y轴于点N，则点T平分ON.

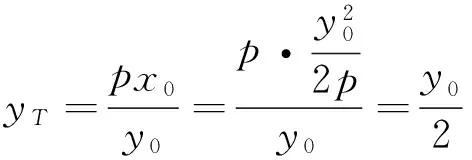
依照上述研究思路，若把性质4中的点O看成是抛物线的一个顶点A，点B看成“无穷远处”的另一个顶点，点P与两个顶点的连线分别交y轴于点M,N，则可以得到椭圆、双曲线中类似的结论：

图5

性质5如图5，点

图6

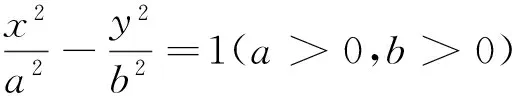
此命题可仿照命题5证得.据此可得圆锥曲线另一统一性质为：

定理2圆锥曲线上任意一点P与左右两顶点A、B的连线分别交y轴于M、N，点P处的切线交y轴于点T，则点T平分MN.

[1]宋广志,邢友宝.抛物线的另一个“顶点”和“焦点”[J].数学通讯，2010,10(下半月)：24-25.

[2]王树茗.何谓无穷远点？圆锥曲线为何需要它？[J].数学通讯，2011,4(下半月)：39-41.