例谈由动点轨迹形成区域的面积求法

江苏省苏州市田家炳实验高级中学　(215004)

周　磊



例谈由动点轨迹形成区域的面积求法

江苏省苏州市田家炳实验高级中学(215004)

周磊

在高中数学学习中，经常遇到一类以动点轨迹构成区域的面积为背景的填空题，这种题型设计新颖，构思巧妙，容易给学生造成思维障碍．因此，加强对这类题型的思路探究，可以开阔学生的解题思路，培养学生的分析思维，提高学生解决问题的能力．本文中，笔者将撷取相关例题细细品评，利用Geogebra软件展示分析过程，与读者交流.

探究1基于坐标变换背景下的区域形成

例1在平面直角坐标系中，已知平面区域A={(x,y)|x+y≤1,x≥0,y≥0}，则平面区域B={(x+y,x-y)|(x,y)∈A}的面积为.

图1

分析:首先利用换元法设出区域B内点的坐标，再根据区域A内点的约束条件求出区域B内点的约束条件，然后画出可行域，最后由三角形面积公式求出答案.

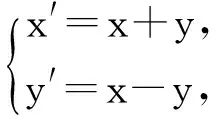
例2直角坐标系中，点集A={(x,y)|x2+y2≤1}，B={(x,y)|x≤4,y≥0,3x-4y≥0}，求点集Q={(x,y)|x=x1+x2,y=y1+y2,(x1,y1)∈A,(x2,y2)∈B}所表示的区域的面积.

图2

解:由x=x1+x2，y=y1+y2，得x1=x-x2，y1=y-y2.∵(x1,y1)∈A，把x1=x-x2，y1=y-y2，代入x2+y2≤1.∴(x-x2)2+(y-y2)2≤1，点集Q所表示的区域是以集合B={(x,y)|x≤4,y≥0,3x-4y≥0}的区域的边界为圆心、半径为1的圆内部分，如图2所示，其面积为5+6+4+3+π=18+π.

图3

探究2基于函数图像变换背景下的区域形成

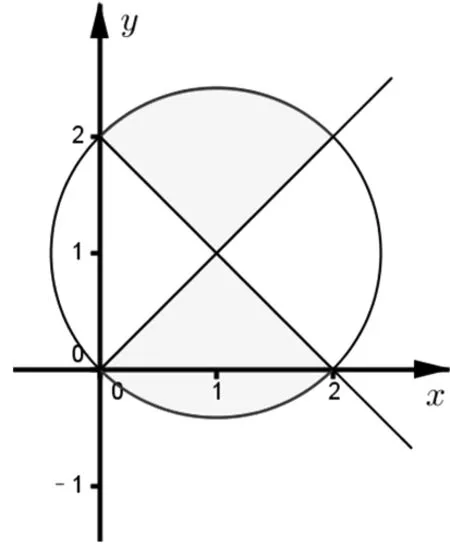
图4

例4已知函数f(x)=x2-2x，则满足条件

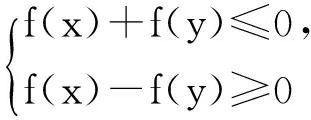
例5已知a,b是实数，函数f(x)=ax+b|x-1|(x∈R)，若a,b∈(-2,2)，且函数f(x)在(0,+∞)内存在最大值，试在平面直角坐标系aOb内，求出动点(a,b)运动区域的面积.

分析:先化简函数，若a,b∈(-2,2)，且函数f(x)在(0,+∞)内存在最大值，则需

图5

解:f(x)=

例6已知函数f(x)=|x2-2|，若f(a)≥f(b)，且0≤a≤b，则满足条件的点(a,b)所围成的面积为.

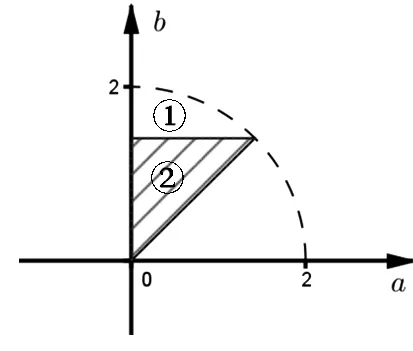
图6

探究3：基于几何图形运动背景下的区域形成

例7如图7放置的等腰直角三角形ABC薄片(∠ACB=90°，AC=2)沿x轴滚动，设顶点A(x，y)的轨迹方程是y=f(x)，则f(x)在其相邻两个零点间的图像与x轴所围区域的面积为.

图7

图8

图9

例9已知集合A={(x,y)|y=x2+2bx+1}，B={(x,y)|y=2a(x+b)}，其中a,b为负实数，且A∩B=∅，则集合{(x,y)|(x-a)2+(y-b)2=1}对应图形的面积为.

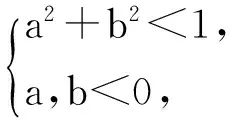
首先，以{(a,b)|a2+b2<1,a,b<0}区域边界上的点为圆心，画出一些圆，得出所求区域的外围边界；再以内部一些点为圆心，同样可画出部分圆；最后发现所有区域中圆轨迹如图10所示.

图10 图11

结语

本文中，笔者利用GeoGebra软件研究了一类关于动点轨迹构成的区域面积问题，这种基于代数背景的几何问题，在解题时，对抽象思维要求较高，会给学生的解题思维造成障碍.基于上述考虑，笔者利用GeoGebra教学软件，可以很直观、动态地展示形成的几何图形；更为重要的一方面在于，笔者基于该软件将此类问题分布转化，分析问题时，可以培养学生借助尺规作图，提升动手能力，培养数学转化思想，从而分析如何优化数学教学过程，探索数学教学新模式.