实践剖析 突破定值问题——2016北京理科第19题的多解及探究

山东省聊城大学数学科学学院(252000)

夏迎雪*作者现为2015级硕士研究生.　于兴江



实践剖析突破定值问题
——2016北京理科第19题的多解及探究

山东省聊城大学数学科学学院(252000)

夏迎雪*作者现为2015级硕士研究生.于兴江

1.原题呈现

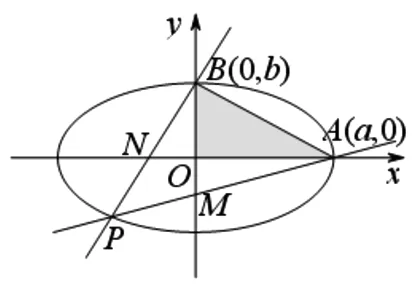
图1

(1)求椭圆C的方程；

(2)设P是椭圆C上一点，直线PA与y轴交于点M，直线PB与x轴交于点N，求证|AN|·|BM|为定值.

2.解法探究

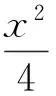
下面讨论第(2)小题的解法(点P异于A、B的情况).

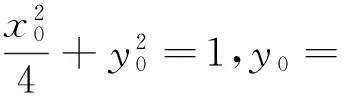
国内某钢厂厚板可逆式3800轧机支承辊，辊面直径2200mm，辊面有效工作长度3700mm，辊体材质70Cr3Mo，重量154t，其中一端辊面严重掉块剥离，最大剥离深度约300mm，掉块轴向长度最大约1650mm，周向长度最大约3000mm。经研究，中信重工决定对支承辊进行堆焊修复，此规格是当时国内堆焊修复的最大规格的支承辊，修复风险非常大。本文采用多种试验分析手段从剥落形态、硬度、化学成分、内部组织等方面对该支承辊辊身剥落掉块问题进行分析，为其堆焊修复工艺的研究做理论支撑。

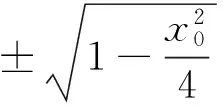
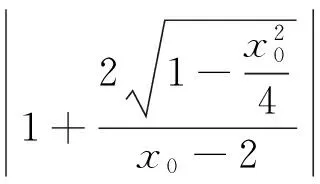
于是|AN|·|BM|

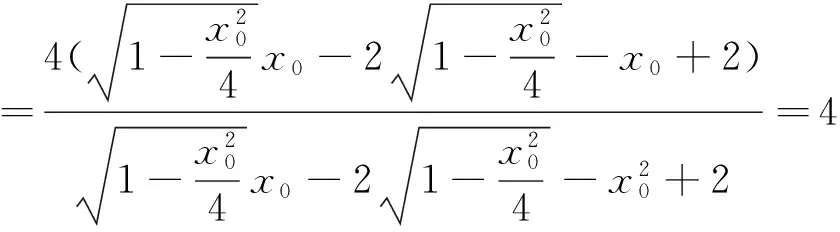
因此，|AN|·|BM|为定值4.

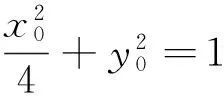
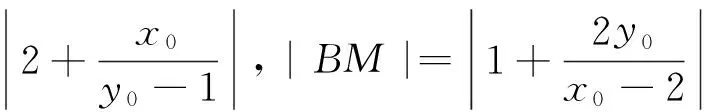
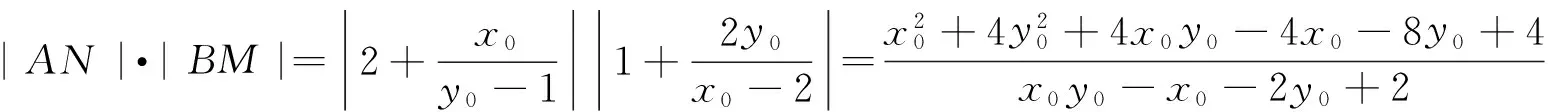
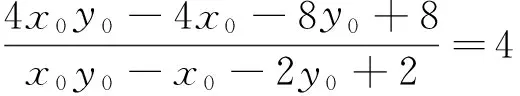
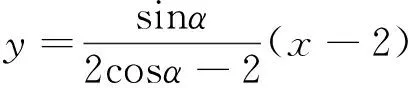
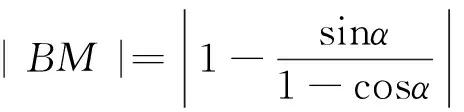
于是|AN|·|BM|

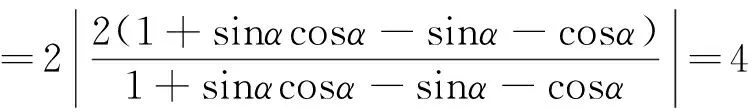
所以|AN|·|BM|为定值4.

3.探究推广

笔者通过几何画板深入探究，发现了椭圆的一个有趣结论，经过进一步观察研究，推广出以下两个定理并给出证明过程.

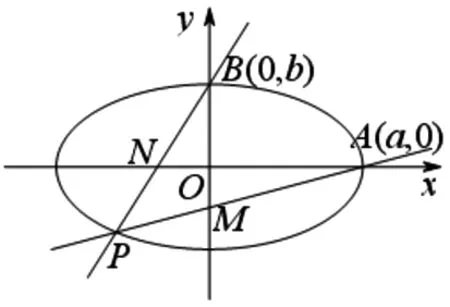
图2

(1)当P与A或B重合时，|AN|·|BM|为定值0；

(2)当P异于A、B时，|AN|·|BM|为定值2ab.

证明：(1)当P与A重合时，直线PA平行于y轴，A、N、P三点重合，|AN|=0，故|AN|·|BM|=0；同理，当P与B重合时，|BM|=0，即|AN|·|BM|=0.

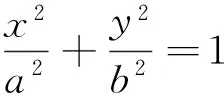
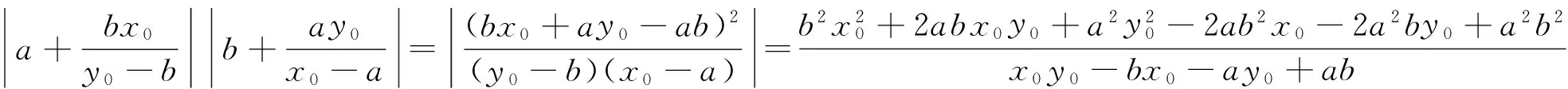
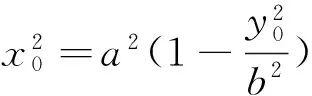
|AN|·|BM|

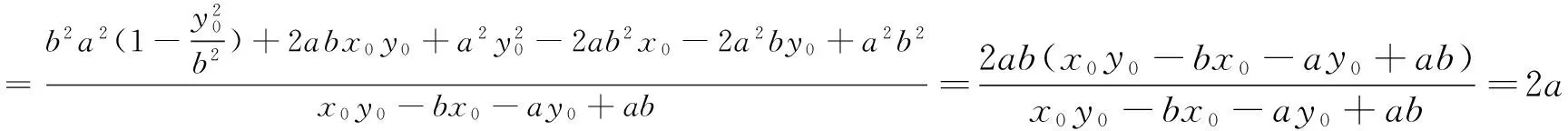
图3

(1)当P与A或B重合时，|AN|·|BM|为定值0；

(2)当P异于A、B时，|AN|·|BM|为定值2ab.

定理2的证明同理于定理1，本文不给出具体证明过程.

[1]姜晓洁，于兴江.对2015年北京高考数学理科19题的推广探究[J].中学数学研究(江西)，2016,4.

[2]孔德泉.年年岁岁题相似，岁岁年年题不同——形散神同的几道高考解析几何题的研究[J].中学数学研究(江西)，2016,5.