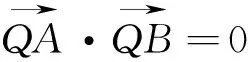众里寻它千百度，那“题”却在“教材”处——例谈高考命题“源于教材”和“回归教材”

安徽省阜阳市太和中学　(236600)

韩长峰



众里寻它千百度，那“题”却在“教材”处
——例谈高考命题“源于教材”和“回归教材”

安徽省阜阳市太和中学(236600)

韩长峰

罗增儒语：教材是课程的载体，因此高考命题最具体、最方便的依据其实是教材．教材是编者集体智慧的结晶，是数学知识和数学思想方法的重要载体，承载着新课程改革的理念和导向，渗透着创新精神和实践能力的培养，同时也体现着高考改革的发展趋向．

高考数学对数学考查大致可分为五个层次：对基础知识的考查，对思想方法的考查，对数学能力的考查，对应用意识的考查和对创新意识的考查.众所周知，高考命题要求“源于教材，高于教材”，其实广义的说，所有的高考试题都是“源于教材”，而本文所说的“源于教材”仅指最初级层次的——对数学基础知识的考查，即试题的题干、题枝、甚至答案都直接出自教材，或者说“照搬”教材的内容.

高考命题又要求“高于教材”和强调“以能力立意”，这使得“源于教材”成为口号，“回归教材”更是空谈.那么到底该怎样“源于教材”又如何“回归教材”呢？笔者就以2015高考广东卷的一试题为例，谈谈个人对数学高考中“源于教材，回归教材”的思考．

1.原汁原味，源于教材

例1(2015年广东卷理科第20题)已知过原点的动直线l与圆C1:x2+y2-6x+5=0相交于不同的两点A,B.

(1)求圆C1的圆心坐标；

(2)求线段AB的中点M的轨迹C的方程；

(3)是否存在实数k，使得直线l:y=k(x-4)与曲线C只有一个交点？若存在，求出k的取值范围；若不存在，说明理由.

赏析:第(2)问是求轨迹方程问题，方法多达十种.追根溯源，查阅教材，笔者发现其“照搬”教材的内容：人教版A版选修2-1第37页A组第4题“过原点的直线与圆x2+y2-6x+5=0相交于A,B两点，求弦AB的中点M的轨迹C的方程.”

无独有偶，2013年安徽卷理科又有一例.

例2(2015年安徽卷理科第3题)在下列命题中，不是公理的是().

A.平行于同一个平面的两个平面相互平行

B.过不在同一条直线上的三点，有且只有一个平面

C.如果一条直线上的两点在一个平面内，那么这条直线上所有的点都在此平面内

D.如果两个不重合的平面有一个公共点，那么他们有且只有一条过该点的公共直线

赏析:选项B、C、D分别是公理2、1、3的“复制+粘贴”，选项A对应的应该是公理4：平行于同一条直线的两条直线平行，此处把直线“置换”为平面，虽然命题A是真命题，但符合题目“不是公理”的要求，所以选A.

2.源于教材，回归教材

落实“源于教材，回归教材”的前提是我们要明确教材里有什么.2016年《全国统一考试大纲的说明》第131页“知识要求”首段：“知识是指《普通高中数学课程标准(实验)》所规定的必修课程、选修课程系列2和系列4中的数学概念、性质、法则、公式、公理、定理以及由其内容反映的数学思想方法，还包括按照一定程序与步骤进行运算、处理数据、绘制图表等基本技能.”那么，教材中的概念、性质、法则、公式、公理、定理以及由其内容反映的简单的数学思想和方法无疑是数学的基础知识.下面赏析近些年“源于教材”的高考试题，从中品味如何“回归教材”.

2.1概念变式的回归

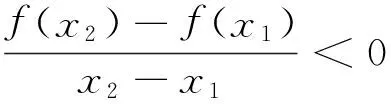
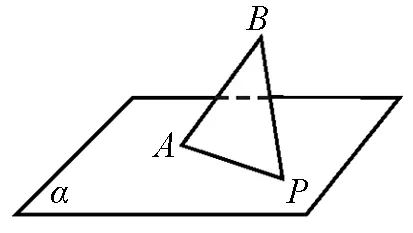
A.f(3)

B.f(1)

C.f(-2)

D.f(3)

赏析：单调性是函数最重要的性质，教材的处理呈螺旋式上升，在必修和选修两次学习.而考题是单减函数教材定义的等价形式，结合函数奇偶性得出答案A，既真正体现“源于教材，高于教材”的命题理念，又有效的考查了考生辨析问题和解决问题的能力.同年理科卷第12题呈现了单增函数定义等价形式“(x2-x1)(f(x2)-f(x1))>0”，这些都是在教材核心概念的基础上稍加变形或类比而命制的试题，体现了命题者的智慧和创新能力，应该是“回归教材”类试题的典范.

2.2公式推导的回归

例4(2010年四川卷理科第19题)

(Ⅰ)①证明两角和的余弦公式Cα+β：cos(α+β)=cosαcosβ-sinαsinβ；

②由Cα+β推导两角和的正弦公式Sα+β：sin(α+β)=sinαcosβ-cosαsinβ.

赏析：新课程标准指出学生的学习过程是在教师的引导下的“再创造”过程,强调知识的生成性，注重知识的来龙去脉.试题2证明两角和的余弦公式，借步推导两角和的正弦公式，紧接着直接运用，这其实就是课堂教学中的一个数学探究环节，符合新课程倡导的“自主探索、动手实践、阅读自学”等学习方式，能较好的考查考生自主探究的能力.

2.3定理证明的回归

例5(2011年陕西卷理科第18题)叙述并证明余弦定理.

赏析：陕西省在高考试题“回归教材”可谓是开拓者，2011年的九字考题“叙述并证明余弦定理”更体现出陕西省命题组的睿智和魄力，既能考查考生的基本数学知识和能力，又具有较好的信度、效度和一定的区分度，这样的考题就是好题.正因为这些试题的出现，使得新课教学把重心转移到教材中的基本概念、重要公式和定理的推导与证明上，这或许正是此类试题的价值和意义.

2.4习题背景的回归

2.5数学素材的回归

图1

例7(2008年浙江卷理科第10题)如图1，AB是平面α的斜线段，A为斜足，若点P在平面α内运动，使得△ABP的面积为定值，则动点P的轨迹是().

A.圆B.椭圆

C.一条直线D.两条平行直线

赏析：例7源自人教版A版选修2—1第42页探究与发现栏目《为什么截口曲线是椭圆》.教材是这样描述的：“用一个与圆柱的母线斜交的平面截圆柱，得到一条截口曲线.你能够证明截口曲线是椭圆吗？”例7的实质是考查椭圆的本质定义，即椭圆是由与圆柱的母线斜交的平面所截得的截口曲线的轨迹.试题以此为背景，使大家感到既在“意料之外”，但又在“情理之中”.无独有偶，2010年浙江卷理科第19题是以人教版A版选修2—3第70页“高尔顿板模型”为背景来设计的高考试题.

2.6方法运用的回归

例8(2003年全国课标卷理17)已知函数f(x)=2sinx(sinx+cosx).

(Ⅰ)求函数f(x)的最小正周期和最大值；

赏析：例8源于教材必修4三角函数“五点法”作图，体现列表-描点-画线等作图步骤，其法在八年级学习一次函数时教材就提及了.每每讲授正弦函数“五点法”作图时都要提到该题，因此“五点法”作图被学生掌握和运用的很好，发挥了很好的导向作用.

3.回归教材，有的放矢

上面赏析了近些年“源于教材”的高考试题，也从中品味到如何“回归教材”，而作为一线的教师更要研究以怎样的“源于教材”来指导落实“回归教材”.

3.1注重教材定理、公式的推导过程

当前，不讲基础而一味钻难题的做法很普遍，忽视教材而陷于题海战的现象大有所在，这有悖于《数学课程标准》的理念．2011年浙江卷理科第5题就是教材例题条件简单的调整，2012年陕西卷理科第18题出现了三垂线定理及其逆定理的证明，2013年陕西卷文科第17题出现等差数列的前n项和Sn的公式推导，理科第17题数学出现等比数列的前n项和Sn的公式推导，……

数学是一种科学的思维方法，要学会思考；数学也是一种操作活动，要熟练技能；数学还是一种问题解决的方法，要学会解题．数学教学不能简单的理解为学生熟记公式、定理和结论，然后进行题海训练，而应是注重定理、公式的推导过程，培养良好的解题习惯、发展分析和解决问题的能力，领悟思维的诱导、调整、进阶、完善，领悟其蕴含的丰富的数学文化、数学方法、数学思想，重新全面梳理知识、方法，促使学生有层次地、递进地理解数学本质，从而提升学生的数学思维素养．

3.2注重教材例题、习题的变式训练

教材例题、习题看似平淡无奇，其实是呈现简洁、极富韵味的好题，值得我们细细品味．数学教学应诱导学生把特殊问题纳入更一般的范围，从特殊推广到一般，揭示事物的普遍规律，促使学生会解一道题到会解一类题，由低层次到高层次，把数学思维提高到由例及类的层次，加速数学思维的优化．

例如，人教版A版选修2—1第73页的第6题:直线y=x-2与抛物线y2=2x相交于A,B两点，求证：OA⊥OB．

分析：其已知条件①直线l:y=x-2是一条定直线，其斜率为1，在x轴上的截距为2；②抛物线C:y2=2x的特征量2p=2，而直线l所过的定点M(2,0)的横坐标恰好为2，巧合？抑或规律？

拓展1直线“活”起来．

①直线l的斜率不变，在x轴上的截距变为1，结论还成立吗？(不成立)

②直线l的斜率变为3，在x轴上的截距不变，结论还成立吗？(成立)

③直线l的斜率变为-1，在x轴上的截距不变，结论还成立吗？(成立)

④直线l的斜率变为k，在x轴上的截距不变，结论还成立吗？(成立)

⑤直线l的斜率不存在，在x轴上的截距不变，结论还成立吗？(成立)……

拓展2曲线“动”起来．

①抛物线C变为C′:y2=3x，其它条件不变，结论还成立吗？(不成立)

②抛物线C变为C′:y2=-2x，其它条件不变，结论还成立吗？(不成立)

③抛物线C变为C′:x2=-2y，其它条件不变，结论还成立吗？(不成立)

④抛物线C变为C′:x2=2y，其它条件不变，结论还成立吗？(不成立)……

拓展3条件共“舞”．

①直线l的斜率变为k，在x轴上的截距不变，抛物线C变为C′:y2=2px(p>0)，结论何时成立？(2p=2)

②直线l的斜率变为k，在x轴上的截距变为4，抛物线C变为C′:y2=2px(p>0)，结论何时成立？(2p=4)

③直线l的斜率变为k，在x轴上的截距变为2p，抛物线C变为C′:y2=2px(p>0)，结论成立？(成立)……

拓展思路4逆化命题.

①直线l与抛物线y2=2px(p>0)相交于A,B两点，若OA⊥OB，直线l有何特征？

②直线l与抛物线C:y2=2px(p>0)相交于异于顶点的两个动点A,B．若OA⊥OB，直线l必过定点吗？……

拓展思路5披上“神秘”外纱.

拓展思路6类比引申.

①原点O是抛物线C的顶点，原点O变为抛物线C上任意一点，是否还有类似的结论呢？

②抛物线C变为圆锥曲线中的椭圆、双曲线，是否还有类似的结论呢？

③抛物线C变为圆，结论是否成立？……

3.3注重教材阅读、探究的思维启示

新课标教材中，充实了许多具有生活气息的阅读材料吸引了学生的注意力，关注了学生的非智力因素对学习的影响，倡导学生的认知与兴趣、情感紧密地联系起来，实现情知并行、情知互动、情知交融，也设置了饶有情趣的探究问题，激发了学生学习的激情，促使学生产生探究的原动力和内在需求．

高中数学教学时，应当对本原性的问题多一些思考，结合教材提供的阅读材料、探究问题的思维启示，创设开放、互动、新型的教学体验环境，促使学生体会知识的发生和发现过程，引领学生学会审题，学会思维，把教材中“省略”的思维信息慢节拍地找寻出来，提升数学探究教学的高效．

3.4注重教材方法、思想的潜移默化

形式化是数学的基本特征之一．在数学教学中，学习形式化的表达是一项基本要求，但是不能只限于形式化的表达，要强调对数学本质的认识，否则会将生动活泼的数学思维活动淹没在形式化的海洋里．新课程为了促进学生对数学内容本质的理解，建立内容本质与形式表达之间的有机联系，使数学形式化过程适应学生的学习心理，并在建构数学形式化认知结构的同时，获得全面发展，在“强调本质，注意适度形式化”方面作出了努力．

高中数学教学应该返璞归真，努力揭示数学概念、法则、结论的发展过程和本质，注重教材方法、思想的潜移默化．数学教学要讲逻辑推理，更要讲道理，通过典型例子的分析和学生自主探索活动，使学生理解数学概念、结论逐步形成的过程，体会蕴涵在其中的数学方法、数学思想潜移默化，把数学的学术形态转化为学生易于接受的教育形态．

正如章建跃语：高考复习，回归教材、回归基础才是正道．作为教师，我们务必将教材视为教学的“红色根据地”，在把握教材、理解教材的基础上，着力揣摩教材的编写意图，明确教材的脉络结构，深刻领悟数学知识的作用和蕴含的人文素养的文化价值，做到跳出教材、活用教材，真正落实“源于教材，回归教材”的科学备考.

[1]史嘉，李振球.从“源于教材”到“回归教材”[J].中小学数学，2013(7-8):84-85.

[2]沈新权.高考数学试题命题策略解读[J].中学数学(高中版)，2013(2):38-39.

[3]岳峻，阮艳艳.探究圆锥曲线的内接直角三角形[J].高中数学教与学，2015(12):34-36.