数学拓展材料设计的常见问题及思考

摘 要：拓展材料是推进学生开展探究性学习的有效载体，它的设计是数学教学设计的重要组成部分.拓展材料的设计关键在于“度”的把握，不仅要依据课程标准，关注学情，还要有效衔接数学思想方法.

关键词：数学教学；拓展材料；探究性学习

数学新课程强调教师要建设性地使用教材，充分利用和开发各种教学资源，为学生提供丰富的学习素材和足够的思维空间，使每位学生得到长足的发展[1].为此，在数学教学中设置延伸拓展材料成为一种常态.而在当前数学教学中，由于教师对数学教学内容、学生知识基础、认知能力等认识不够，导致出现拓展材料设计过偏、过难、过深，从而使学生的数学学习出现困难，教学出现低效乃至负效的情形.下面就以南京市初中数学课堂中的一些教学设计片段为例（使用的教材为江苏科技出版社出版的《义务教育教科书·数学》），谈谈数学拓展材料设计中的常见问题.

一、忽视学生知识基础 欲速不达

有效的拓展材料设计一定要从学生已有的数学知识基础出发，要关注不同学段数学教学内容特点，设计的问题要符合学生阶段性的认知水平和解决问题的能力，如果拓展材料中的问题过难、过深、过于超前，那么学生难以企及，会望而生畏，以至于学生对数学理解产生偏差和困难.

案例 1 《6.1 函数》（八年级上册）第1课时

在本节课小结前，教师出示如下拓展问题：

（1）当x是实数时，y=1，y是x的函数吗？

（2）当x是有理数时，y=0；当x是无理数时，y=1，y是x的函数吗？

在教学中，几乎整班学生都认为上述y不是变量，与函数定义中x、y都是变量不符，因此得出它们都不是函数的结论.

本课是南京市某校教学开放日开设的教学公开课，事实上问题（1）是常数函数，问题（2）是狄利克雷函数，这两个函数若放到高中学习了建立在集合基础上的函数概念后，就十分容易理解.因此在初中数学教学中，一般暂时不涉及这些函数，更多研究的是一些常见函数：一次函数、反比例函数、二次函数等，这类问题可以放到高中阶段的数学学习中去研究.

案例2 《9.3 平行四边形》（八年级下册）第2课时

在“思维拓展”阶段，教师出示问题：

如图1，已知直线l及l外一点A.请你只用圆规在直线l外画出一点P，使得点A、P所在直线与直线l平行.

这是南京市初中数学公开课试讲时设计的一个拓展问题.本课主要的教学内容是平行四边形的两个判定定理，由于学生刚学平行四边形，都把平行四边形作为一个整体来认识，而本拓展问题恰恰是要构造两个全等三角形拼成一个平行四边形，即在直线l上任取B、C两点，以点A为圆心，BC长为半径画弧，再以点C为圆心，AB长为半径画弧，两弧交于点P.这一操作的核心在于平行四边形是由两个全等三角形构成，对初学平行四边形相关知识的学生来说，仅仅用圆规来寻找点P的难度太大，而这些知识会在三角形中位线部分得到相应强化，因此课后研讨中，建议这一拓展问题可以放至本章的复习课教学中.

二、忽视教学目标约束 过犹不及

课堂教学目标是通过一节课的教学，学生要达到双基、能力和态度的变化，它是落实课程标准的可操作、可观察的微观目标.课堂教学目标依据课程标准，但不囿于课程标准，它有适度的弹性，但又受课程标准的约束.好高骛远，不顾学生的学习状况和课程标准的要求，不切实际地追求过高过远的目标，往往会偏离正常的教学轨道，挫伤学生的学习积极性和主动性.

案例3《9.5 多项式的因式分解》（七年级下册）第4课时

在本节课小结前，教师出示如下拓展问题：

已知a、b、c是△ABC三边的长，a2-16b2-c2+6ab+10bc=0，试用因式分解知识说明a+c=2b.

这是南京市初中数学联片教研活动中开设的公开课片段.本课的主要任务是综合运用“提公因式法”和“运用公式法”，将多项式分解因式.现行教材中已不涉及用“分组分解法”将多项式分解因式的知识，而本题求解过程中，需将a2-16b2-c2+6ab+10bc=0变形为（a2+6ab+9b2）-（25b2+10bc+c2）=0，即（a+3b）2-（5b+c）2=0.然后利用平方差公式和三角形两边之和大于第三边的知识说明a+c=2b.这一拓展问题超出课程标准内容要求，知识上的落差造成几乎所有学生无从下手.课后研讨中，大家一致认为应弃用这个拓展问题.

案例4《6.4 探索三角形相似的条件》（九年级下册）第2课时

在“思维拓展”阶段，教师出示问题：

如图2，在平面上，给定半径为r的圆O，对于任意点P，在射线OP上取一点P'，使得OP·OP'=r2 ，这种把点P变为点P'的变换叫作反演变换，点P与点P'叫作互为反演点.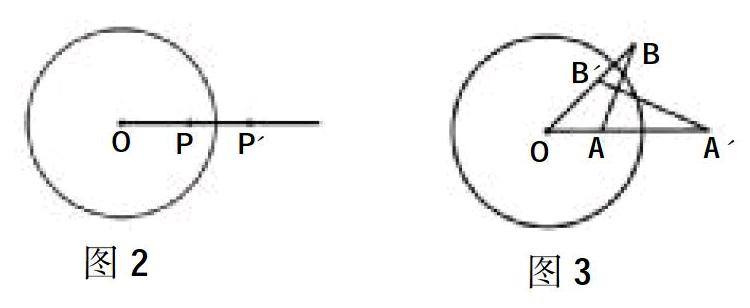

（1）如果一个图形上各点经过反演变换得的反演点组成另一个图形，那么这两个图形叫作互为反演图形.如果不经过点O的直线l与⊙O相交，那么它关于⊙O的反演图形是一个什么图形？

（2）如图3，⊙O内外各一点A和B，它们的反演点分别为A'和B'.那么∠A'与∠B相等吗？为什么？

这是南京市数学骨干教师公开课中的教学设计，本节课学生的主要任务是探索三角形相似的条件：两边成比例且夹角相等的两个三角形相似，而本案例中的拓展点，放在一个学生陌生的几何变换背景下，即反演变换，这是一种比较复杂的变换，目标的偏离也成为困扰学生学习的难点，而其中有关三角形相似的问题，缺乏思维的深度与厚度，因此作为“思维拓展问题”名不副实.

三、忽视方法衔接铺垫 揠苗助长

数学拓展材料大多包含一些探究性和挑战性问题，需要学生综合运用数学知识加以分析解决，其中渗透了一定的研究方法，这里除了研究问题的一般方法，如从特殊到一般的方法，从合情推理到逻辑推理的方法等，还有解决问题的常用方法，如解决问题过程中的建模、归纳和类比等方法 [2].因此教师在拓展材料的设计时，如果忽略解决问题中的数学思想方法的前期铺垫和渗透，没有使方法学习在教学中凸显出来，那么常常会超越学生的经验和能力，使问题解决难以为继.

案例5 《12.1 二次根式》（八年级下册）第1课时

上课后，教师请学生用带根号的式子表示几个简单问题，归纳得出二次根式的概念，通过研究这一概念的内涵、外延、性质，伴随几个例题，教师最后提出拓展问题：

对于根式，你打算如何开展研究？

这是南京市初中数学公开课试讲时设计的一个拓展问题，教师的本意是让学生提炼一下数学研究的一些方法.但由于学习过程都是在教师引导下进行的，并且学生初学二次根式，高度关注知识内容，无暇顾及研究数学的方法，更谈不上知识方法的融会贯通，因此三次根式的出现大大出乎学生意料，教师询问几个学生均无从回答，最后教师只能自述，失去了让学生“思考”的价值.在课后研讨时，参与听课的教师建议删去这个拓展问题或放在本章“小结与思考”教学时再使用.

案例6《5.2 平面直角坐标系》（八年级上册）第1课时

在“思维拓展”阶段，教师出示问题：

已知x是实数，求│x-4│+│x+1│的最小值.

这是南京市初中数学青年教师优质课评比时的拓展问题设计，这一问题改编于课本“习题”中的题目：

点M（4，0）到点N（-1，0）的距离是 .

由于解决上述拓展问题时，需要将两个绝对值转化为数轴上一个动点P（x，0）到两个定点M、N之间的距离和问题，并且要将动点P（x，0）放置于到点N的左边、点M的右边、点M与点N之间进行考察，这里涉及数形转化、图形建构、分类讨论等数学思想方法，超越学生的经验和能力，与本课的教学内容失去应有的匹配度，因此给本节课的教学带来不应有的困难.实际上这个拓展问题可以放至本章复习课教学时作为课后思考题使用.

综上，设计数学教学拓展材料，不仅要准确评判学生的数学现实，还要把握课程标准和教学要求，这些都需要教师的实践智慧，这里的难点是把控好延伸拓展材料的难度、深度和广度，这样才能营造学生“跳一跳，够得着”的情境，使延伸拓展材料真正有效地为教学服务，为学生的发展服务.

参考文献：

[1]朱建明.数学教学中设置延伸拓展材料的思考[J].中国数学教育（初中版），2008（12）：4.

[2]朱建明.数学探究活动设计中的常见问题及有效改进[J].教学与管理，2010（5）：50.