风屏障对车桥组合状态下中间车辆气动特性的影响*

邹云峰， 何旭辉， 李　欢， 秦红禧， 史　康， 黄永明

(1. 中南大学土木工程学院，湖南 长沙 410075；2. 高速铁路建造技术国家工程实验室，湖南 长沙 410075；3. 中国建筑第五工程局有限公司，湖南 长沙 410004)



风屏障对车桥组合状态下中间车辆气动特性的影响*

邹云峰1,2,3， 何旭辉1,2， 李欢1,2， 秦红禧1,2， 史康1,2， 黄永明1,2

(1. 中南大学土木工程学院，湖南 长沙 410075；2. 高速铁路建造技术国家工程实验室，湖南 长沙 410075；3. 中国建筑第五工程局有限公司，湖南 长沙 410004)

设置风屏障是提高行车安全的有效措施之一，但防风效果受风屏障参数、周围环境等多种因素影响。基于同步测压方法，结合本征正交分解技术对风压测点进行加密后通过积分获得气动力，以京沪高速铁路典型高架桥和CRH2列车为背景，研究多种风屏障参数对典型车桥组合状态下中间车辆气动力和风压分布的影响。研究结果表明：测压积分可获得与天平测力精度相当的气动力；风屏障对上游列车的防风效果显著，下游列车气动特性则受之影响较小；相对而言，风屏障透风率大小对列车气动特性影响较大，高度影响较小，且二者存在一个最优组合；设置风屏障后，尽管平均气动力会减小，但最大气动力由于特征紊流的影响可能会增大，风屏障参数应通过风洞试验或数值模拟慎重选取。

高速列车； 风屏障； 车桥组合； 中间车辆； 气动特性

引　言

随着高速铁路的迅速发展，高速列车在侧风作用下的行车安全受到人们的广泛关注[1-2]。提高行车安全的措施有软件措施(即运行管制)和硬件措施(如设置风屏障、优化车体外形及新建线路等)两种，但通过限速慢行或停止运行的管制措施来提高行车安全会影响运送效率，带来巨大的经济损失，因此设置风屏障是提高既有线路列车行车安全的有效措施，且国内外均有成功实施的实例[3-4]。

多年来，国内外学者对风屏障的防风效果进行了广泛研究。王厚雄等通过实测与试验研究表明，风屏障高度达到0.56倍车辆高度时，车辆倾覆力矩接近零，同时指出防风效果受周围环境影响较大[5]；向活跃等通过风洞试验和数值模拟研究风屏障对三种典型线路轨道上方风压分布的影响，发现迎风侧风屏障可有效减小轨道上方的风压，而背风侧风屏障则会增加轨道上方的负压[6]；梁习锋等通过数值模拟方法对路堤上不同设置位置处的挡风墙合理高度进行研究，发现不同位置处的风屏障合理高度不一样[7]；周奇等通过数值模拟对设置风屏障后车道中心处的流场进行研究，表明防风效果随透风率增大的变化趋势并非线性，而有一个最优透风率[8]；Coleman通过风洞试验研究了不同形状风屏障的防风效果，认为风屏障能有效降低车辆气动力，但防风效果还与车辆外形有关[9]；Papesch研究了风屏障形式对车辆倾覆力矩的影响，并得到了合理的风屏障形式[10]；Kwon等通过对设置风屏障后桥面流场的测试发现风屏障高度达到桥面宽度的1/8时可使桥面风速减小一半[11-12]；Kozmar通过PIV技术研究了风屏障对桥面流场的影响，发现风屏障能有效减小桥面处的风速[13]；日本学者对风屏障防风性能的研究结果表明，风屏障高度、透风率等参数最优值的选取与路基、桥梁等下部结构及周围地貌等因素有关，应通过风洞试验确定[14]。

由上述综述可看出，已有研究成果大多通过测试线路上方流场或车辆整体平均气动力来考察风屏障的防风效果，但流场测试通常没有考虑线路上的车辆，得到的结果只能反映风屏障对线路上方流场的影响，而忽略了车辆对风屏障-线路系统流场的干扰；至于平均气动力的测试，未能考虑风屏障产生的特征紊流对脉动气动力的影响，且由于给出的是车辆整体气动力，故不能探究风屏障对车辆风压分布的影响，难以深入认识风屏障对列车气动特性的影响机理。此外，防风性能受下部结构形式及周围环境影响是众多研究者已达成的共识。鉴于高架桥在中国高速铁路线路中的比重通常较大，本文以京沪高速铁路典型高架桥和CRH2列车为背景，通过同步测压技术对典型车桥组合状态下中间车辆风压分布进行测试，比较风屏障高度、透风率等参数对列车气动特性的影响。研究成果可为中国类似线路风屏障的设置提供参考。

1　风洞试验概况

1.1试验模型

试验研究的列车、桥梁原型分别为CRH2型客车(头车+中间车辆)和32 m简支梁桥(5跨)，为满足堵塞率要求，模型几何缩尺比为1∶25(最大堵塞率为4.2%<5%)，头车模型尺寸为1028 mm(长)×140 mm(宽)×135.2 mm(高)，中间车辆为1000 mm(长)×140 mm(宽)×135.2 mm(高)，桥梁模型尺寸如图1所示。试验模型与实物在外形上保持几何相似，并考虑了轨道、转向架及车轮等，以尽可能真实模拟实际气流的绕流特征。列车和主梁模型采用优质木材制作，桥墩及其他部件由钢材制作，保证模型具有足够的强度和刚度，在测压试验中模型不发生变形且不出现明显的振动现象以保证压力测量的精度。试验模型照片如图2所示。

图1　桥梁模型几何尺寸(单位：mm)Fig.1　Geometric dimensions of the bridge model (Unit: mm)

图2　试验模型照片Fig.2　Test model

由于头车外形复杂，横风作用下三维绕流特性显著，而中间车辆外形相对较规则，由测压积分得到的气动力精度易得到保证，且中国动车编组最长达16列车，中间车辆气动力结果可反映至整车。因此本文试验仅在中间车辆布设170个压力测点，每个断面布置17个测点，且各断面测点位置基本一致，测点编号及与来流相对位置如图3所示。

图3　中间车辆测点布置Fig.3　Pressure taps number on middle vehicle

1.2测试设备

风洞试验在中南大学“高速铁路建造技术国家工程实验室”的高速铁路风洞试验系统进行，该系统包括高速和低速两个试验段，其中，高速试验段长15.0 m，宽3.0 m，高3.0 m，试验风速在5～94 m/s范围内连续可调；低速试验段长18.0 m，宽12.0 m，高3.5 m，试验风速在2(20 m/s范围内连续可调。风压测量采用美国PSI公司的DTC net电子式压力扫描阀系统，每通道测试精度达到0.05%。参考点的风速则由皮托管测量。采样时长30 s，采样频率330 Hz。

1.3测试工况

研究表明[15]，列车受到的气动力大小与其所处周围环境有关，因此本文考虑“单车+桥”和“双车+桥”两大类车桥组合状态，测试工况安排及列车位置描述见表1。为研究风屏障高度、透风率对车-桥系统气动特性的影响，选取的实际风屏障高度H分别为2.0，2.5,3.0m，与列车高度之比分别约为0.57，0.71，0.86，每种高度的风屏障考虑0%,10%,20%,30%和40%五种透风率(如表2所示)，其中开孔方式采用方孔阵列式，并在风屏障上均匀分布。本次试验在低速试验段内的均匀流场中完成，试验风速UH(无穷远处参考点高度处的来流风速)为10 m/s，仅考虑90°一个风向角(即横风)。

2　数据处理

测点i处的风压系数Cpi(t)定义如下[16]

(1)

式中Pi(t)为风洞试验中压力扫描阀测得的i点处风压时程，以压力作用方向指向结构表面为正，离开为负；P0为无穷远处试验参考高度处的静压；ρ为空气密度，取ρ=1.225 kg/m3。

压力系数反映的是结构某一点的受力情况，为考察结构受到的整体气动力，可将压力系数对面积积分得到各种气动力系数，如侧力系数CY(t)、升力系数CZ(t)和倾覆力矩系数CMx(t)，其定义分别如下[17]：

表1　测试工况

(2)

(3)

(4)

式中H,B,L分别为模型的高、宽、长；FY,FZ,Mx分别为体轴系下模型受到的侧力、升力和倾覆力矩，由风压积分得到，各气动力方向规定如图4所示，其中倾覆力矩以下游轨道为参考点。

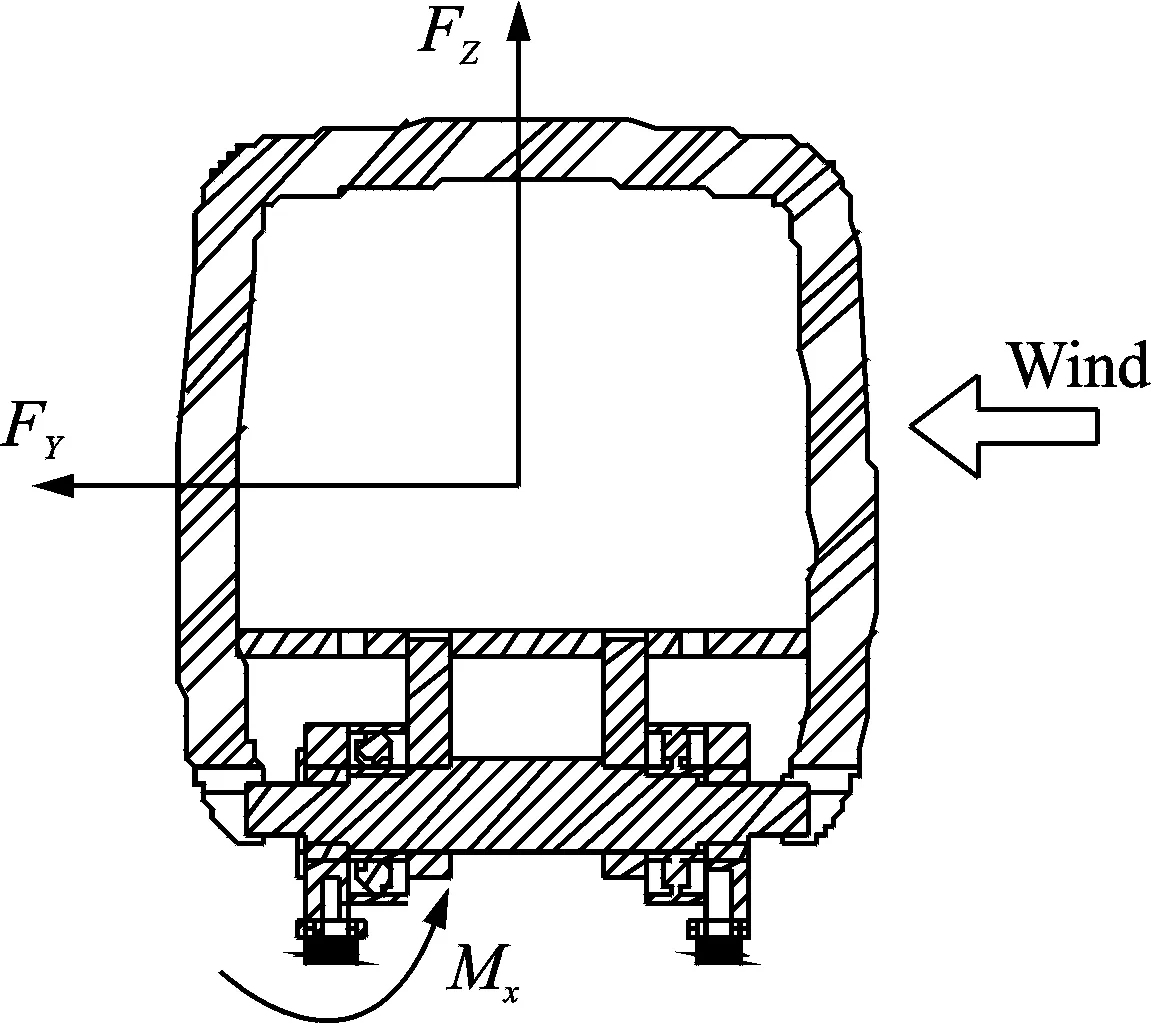
图4　体轴系下列车气动力Fig.4　Aerodynamic force in body axis

根据式(1)～(4)定义的力系数时程，对其进行时间平均可得到平均值，极值计算方法为[16]

(5)

式中Fextreme为式(1)～(4)定义的各种力系数极值；Fmean为力系数均值；g为峰值因子，取g=2.5；σF为力系数根方差；“±”为保证σF与Fmean同号。

测压试验中，模型表面的风压通常需要由一定长度的测压管道传输至压力传感器(本文所用管路长度均为60 cm，内径为1 mm)，在这一传输过程中，传感器测得的脉动压力信号实际上是模型表面真实风压发生畸变后的信号，而反演修正是减小畸变的有效方法之一。反演修正的前提是准确获得测压管路系统的频率响应函数，本文在试验前采用比较法对所用测压管路系统的频率响应函数进行测试[16]。风压测量完成后，采用测得的频率响应函数对各测点的风压信号进行反演修正，以保证由风压积分得到气动力结果的可靠性。

表2　风屏障模型几何参数

3　测压与测力结果对比

为验证测压方法获得列车气动力的可靠性，通过测压与测力试验同时测试中间车辆的气动力，且测力采样参数与测压试验保持一致。试验时，将测力天平底端固定在风洞转盘上，上端固定一块宽30 cm、厚1 cm的木板以安装中间车辆模型，而安装头车模型的木板则直接支撑在风洞转盘上，且二者保持一定间隙以保证头车气动力未传递给天平，考虑到安装模型的木板有一定厚度，为尽可能减小它对天平测力结果的干扰，在其两边固定斜坡以减小木板受到的风荷载，斜坡与木板尽可能接近但又保证不接触，试验照片如图5所示。

图5　中间车辆气动力测压与测力对比试验Fig.5　Test of dynamometer and pressure measurement

风压测点越密，由风压积分获得的气动力精度越高，但压力扫描阀通道数通常有限。本征正交分解(POD-Proper Orthogonal Decomposition)法将随机风压场分解为与空间相关的本征模态和与时间相关的主坐标，根据需要加密点的坐标对本征模态进行空间插值后，结合本征正交分解得到的主坐标便可对没有布置测点处的风压时程进行预测，即对风压数据点进行加密，该方法已经被成功应用于建筑结构风压点的加密。本文将中间车辆测点加密为34×20=680个测点。图6给出的是中间车辆气动力测力与加密风压点后测压积分结果对比，由图可见，测压积分得到的平均气动力随风向角变化趋势与测力结果基本一致，且二者大小相当，相差在±0.1以内，除风向角较小(小于40°)时，由于列车气动力较小，二者偏差百分比(偏差百分比=(测压积分结果-测力结果)/测力结果)大于10%外，其他风向角下均小于10%，表明只要布置适当数量的测压点，通过风压积分也可获得与测力试验相当精度的气动力测试结果。

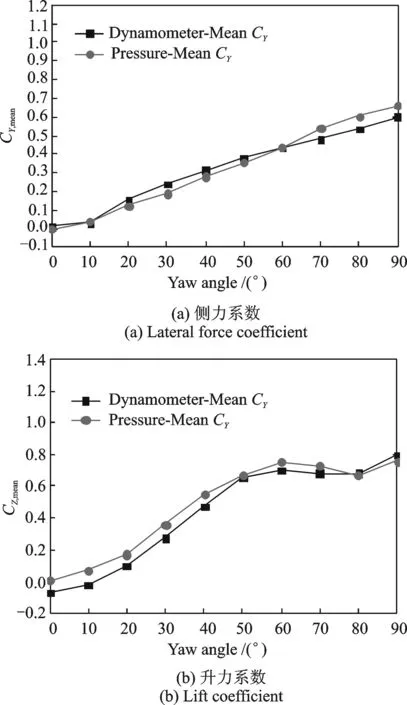
图6　测压积分与测力气动力测试结果对比Fig.6　Comparison of dynamometer results with pressure integration results

图7　风屏障高度对气动力的影响(Case 1)Fig.7　Influence of wind barrier height on aerodynamic force(Case 1)

4　风屏障对列车气动力的影响

4.1高度的影响

为便于直接比较防风性能，本文给出的是有风屏障时的气动力与无风屏障时的比值。图7所示为风屏障高度对列车气动力的影响(以Case 1为例)，可以看出，列车气动力随风屏障高度的增大而略有减小，但减幅与透风率大小有关；从气动力随风屏障高度的变化趋势来看，当风屏障达到某一高度后，气动力将趋于稳定(以侧力尤为明显)。事实上，李永乐[18]的试验结果也表明设置某些高度的风屏障后，列车气动力反而会增大。因此笔者认为各透风率下均可能有一个最优高度，当风屏障高度小于最优高度时，气动力随高度的增加而减小，超过最优高度后，气动力将基本保持不变甚至增大。要证实这种推测，需进行更高风屏障下列车气动力的测试。限于篇幅，该工作将在后续研究中开展。

不同车桥组合状态下列车气动力随风屏障高度的变化情况如图8所示，可以看出，不管是单车还是双车交会，上、下游列车气动力总体随高度的增加而略有减小，但上游列车的减幅小于下游列车，即使是同处于上或下游，气动力减幅也与透风率大小有关。需要说明的是，图8(a)中Case 4变化趋势与其他曲线不一致，这是因为Case 4测试列车位于双车交汇的下游位置，由于上游列车和风屏障的遮挡效应，下游列车平均气动力很小，但随着风屏障高度的增加，其引起的特征湍流增大列车脉动气动力，故其极值可能增大，因此出现图8(a)中Case 4曲线随风屏障高度增加而增大的现象。

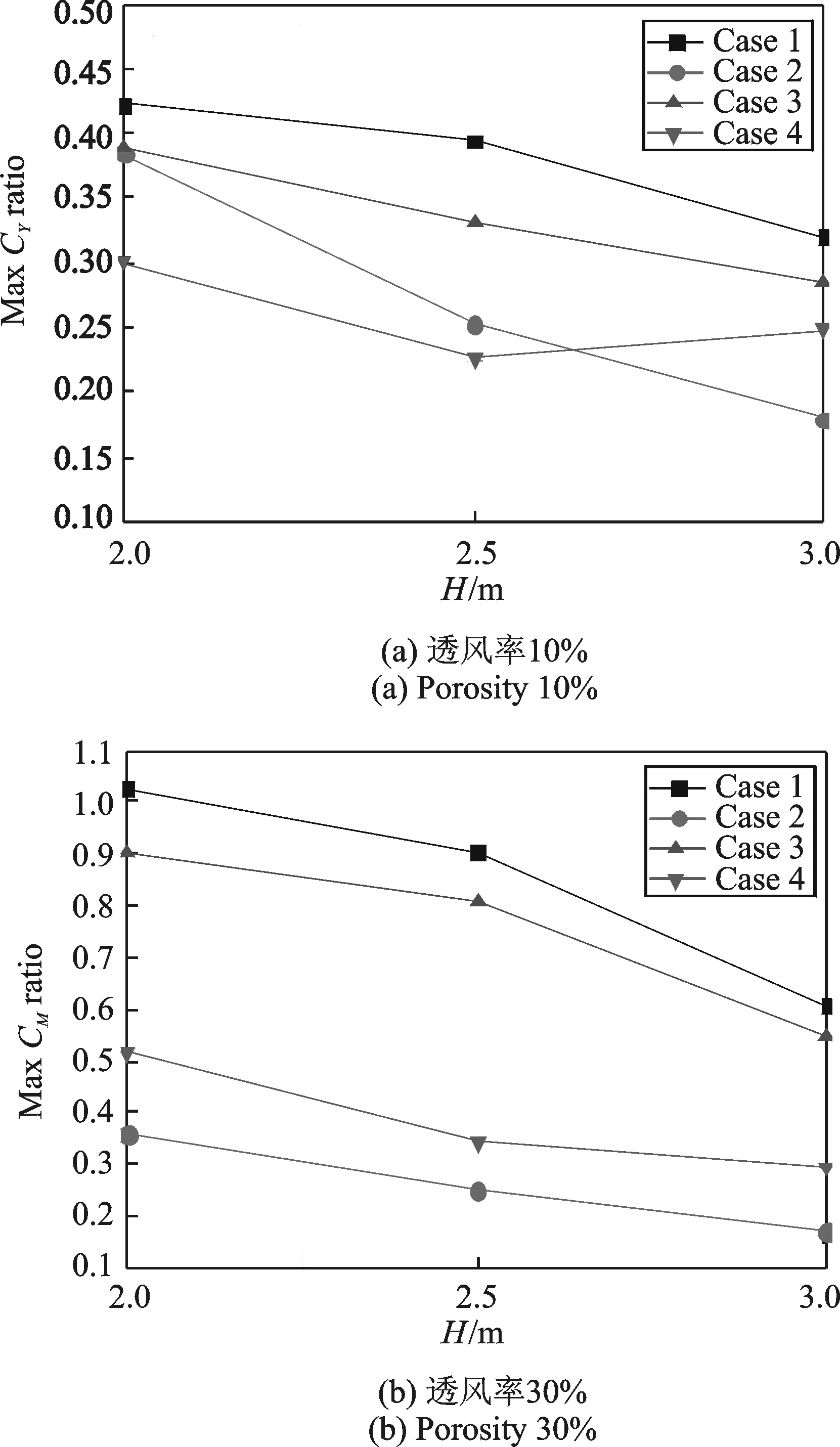
图8　列车位置的影响Fig.8　Influence of train positions

4.2透风率的影响

由上一小节可知，在本文研究的风屏障高度范围内，风屏障高度变化对列车气动特性影响较小，因此仅以H=2.5 m为例，分析风屏障透风率对列车气动力的影响情况。图9为Case 1试验结果，由图可知，列车气动力随透风率的增大呈线性增长关系，在透风率为0时最小，均值甚至接近零；在40%时最大，升力、倾覆力矩甚至比没有风屏障时还大。因此设计师需要特别注意风屏障参数的选择，如果选取不当，不仅不能起到防风效果，反而会增加列车气动力，不利于行车安全。风屏障对最小气动力的防风效果最好，即使是40%透风率，最小气动力也较无风屏障时约小50%，平均气动力次之，最大气动力最差。此现象可解释为，尽管风屏障的遮挡效应使得平均气动力会减小，但由于其产生的特征紊流，气动力均方差会增大，使得极值有所增大，若以平均气动力评价防风性能，会低估最大气动力约20%。倾覆力矩与侧力的变化趋势不一致，说明侧力作用点位置随透风率的变化发生改变，尽管侧力减小，但由于其作用点位置上移，倾覆力矩可能会增大。

图9　风屏障透风率对气动力的影响(H=2.5 m,Case 1)Fig.9　Influence of porous ratio on aerodynamic force(H=2.5 m,Case 1)

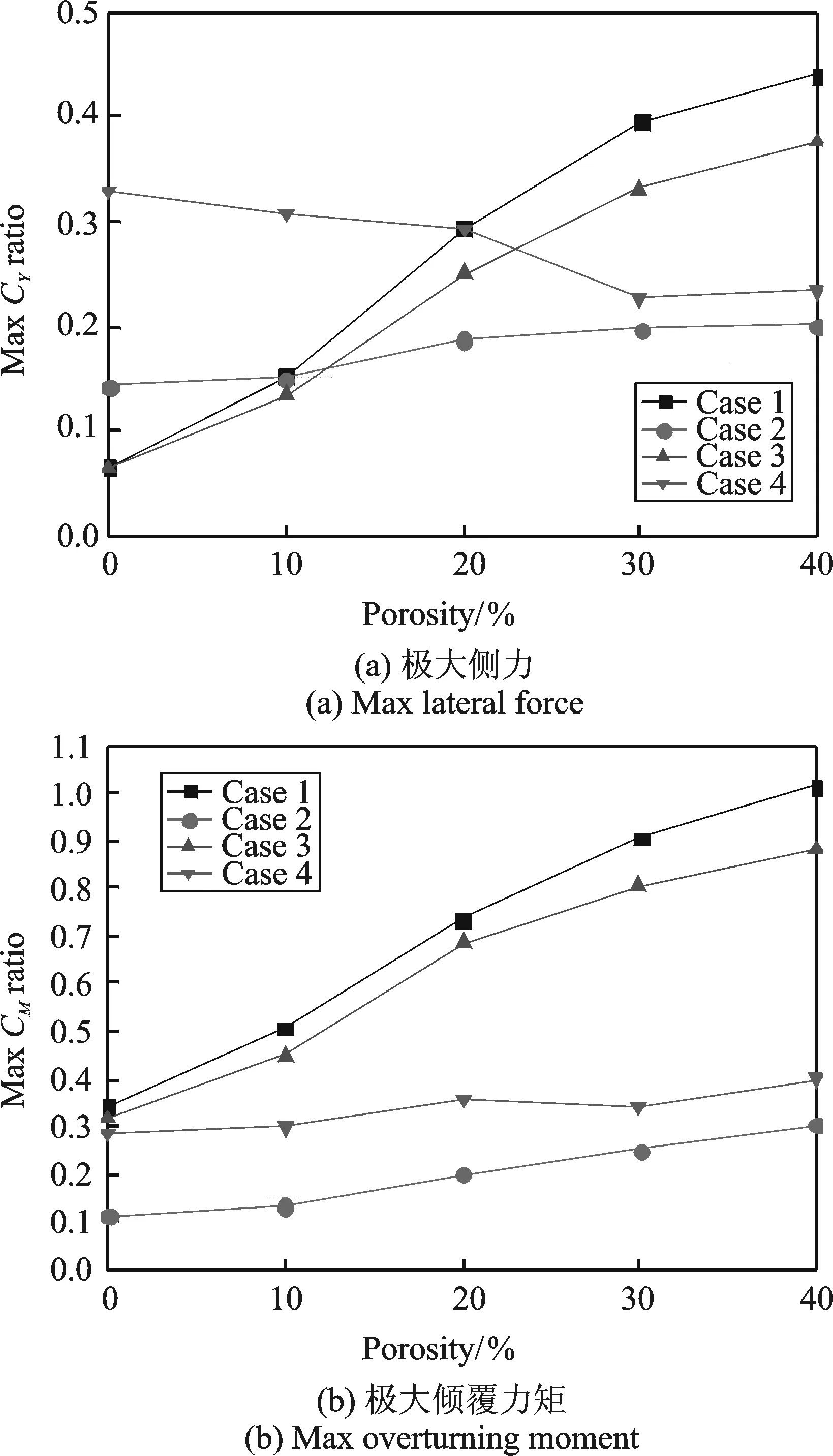
图10　列车位置的影响(H=2.5m)Fig.10　Influence of train position on aerodynamic force(H=2.5m)

不同车桥组合状态下列车气动力随透风率的变化情况如图10所示(H=2.5 m)。从图中可以发现，不管是单车还是双车交会，上(下)游列车气动力随透风率大小的变化趋势基本一致，上游列车气动力随透风率的增加而增大，下游列车则受透风率大小影响相对较小，这是因为上游列车气动力取决于来流大小，而下游列车处于桥梁或上游列车的尾流中，受来流影响较小；双车交会时，上游列车(Case 3)气动力减幅较单车(Case 1)大，下游列车(Case 4)减幅则较单车(Case 2)略微偏小，表明风屏障产生的尾流和列车尾流的相互作用对上下游列车影响不同。需要指出的是，由于上游列车的遮挡效应，Case 4侧力为负值(即侧力方向为逆流方向)，风屏障透风率为0时，列车侧力达到最小值，随着透风率增加，侧力略有增大，但仍为负值，即侧力绝对值随透风率增加而减小，由于图10(a)反映的是侧力比值，故该图中Case 4曲线随透风率的增加而略有降低。

5　风屏障对列车风压分布的影响

5.1高度的影响

笔者前期研究表明[17,19]，中间车辆风压沿列车长度方向均匀分布，因此本文取各截面的风压平均值作为代表性曲线，分析风屏障参数对代表性曲线的影响。图11所示为风屏障高度对列车风压分布的影响(透风率为30%)。由图11可知，风屏障高度对平均风压的影响与列车所处上下游位置有关，上游列车背风面风压基本不受风屏障影响，其他各面的风压均较无风屏障时显著减小，且除车顶的最小负压随风屏障高度的增加而增大外，迎风面和车底风压受风屏障高度大小影响较小；下游列车迎风面与车底的风压较无风屏障时减小，但车顶与背风面却略有增大，相对上游列车而言，下游列车各面风压随风屏障高度变化较小；风屏障高度对最大风压影响相对较小，与平均风压不同的是，车顶的最大风压较没有风屏障时大，且峰值随风屏障高度减小。

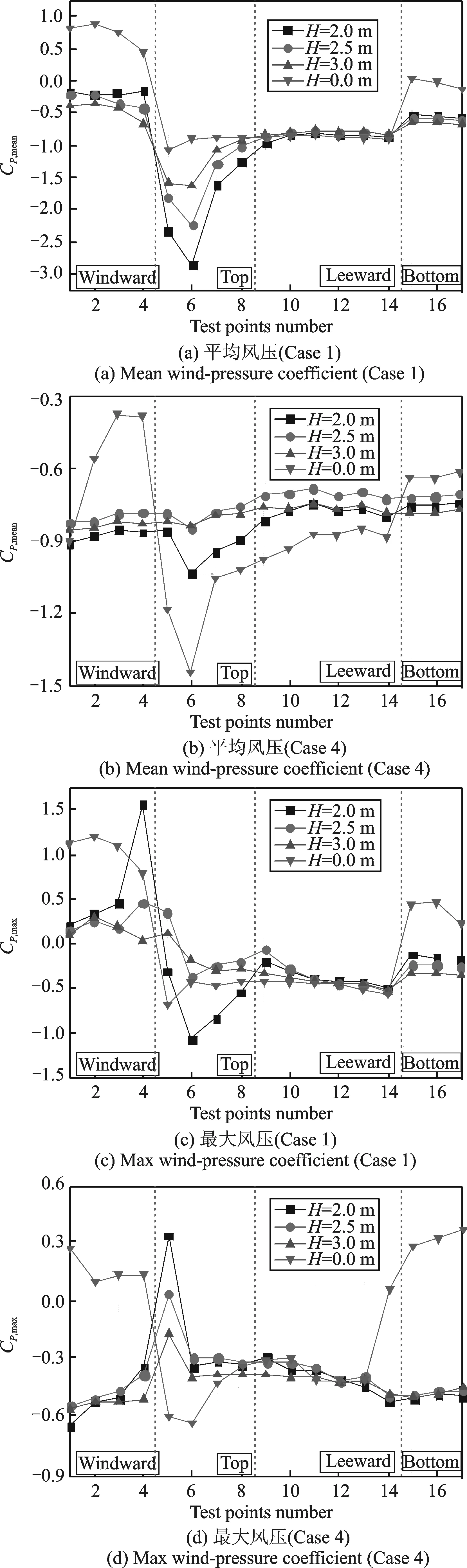
图11　风屏障高度对风压分布的影响(透风率30%)Fig.11　Influence of wind barrier height on distribution of wind pressure (Porosity 30%)

5.2透风率的影响

图12　风屏障透风率对风压分布的影响(Case 1)Fig.12　Influence of porous ratio on distribution of wind pressure (Case 1)

图12所示为风屏障透风率对列车表面风压分布的影响情况(以H=2.5 m,Case 1为例)可以看出，迎风面、背风面及车底的，各风压特征值随透风率的变化趋势基本一致，但车顶的最大风压与之显著不同；设置风屏障后，迎风面风压显著减小，甚至由正变负(透风率为0时，平均风压约为-1.0)，且沿高度分布基本不变，但随透风率的增加逐渐增大；车顶平均和最小风压显著减小，且最小负压发生的位置向下游移动(由5#点移至6#点)，需要指出的是，在透风率为0(40%范围内，最小负压随透风率的增加而减小，但它的最大值出现在透风率为100%(无风屏障)，表明透风率存在一个最优值，当透风率超过该值后，最小负压会随透风率的增加而增大，这一结果与文献[8]的结论一致；至于车顶最大风压，大多比没有风屏障时大(以5#测点尤为明显)，这是因为该区域由于列车气流分离漩涡和风屏障尾流漩涡的相互作用，尽管平均风压减小，但由于脉动增强，不难理解最大风压变大；背风面风压受风屏障影响较小，这是因为该区域风压主要由列车自身产生的尾流决定；车底风压受风屏障影响相对较小，随透风率增加略有增大。

为进一步分析风屏障透风率对下游列车气动特性的影响，Case 4的风压分布见图13(H=2.5 m)。由图可见，各透风率下的风压分布规律基本一致，且风压大小与透风率大小并无明显规律。总的来说，设置风屏障后，下游列车的风压分布更为均匀，但透风率大小对下游列车的风压分布影响较小。

图13　风屏障透风率对风压分布的影响(Case 4)Fig.13　Influence of porous ratio on distribution of wind pressure (Case 4)

6　结　论

(1) 结合POD方法对风压测点加密，由风压积分可获得与天平测力精度相当的气动力，证明了测压积分测试列车气动力的可靠性，这为列车气动力测试提供了一条新的思路。

(2) 设置风屏障后，上游列车迎风面风压、车顶平均和最小风压显著减小，但均随透风率增加而增大，背风面和车底风压则受风屏障影响较小，车顶最大风压由于紊流脉动增强，最大风压大多较无风屏障时大；下游列车的风压分布更为均匀，且受透风率大小影响较小。

(3) 上游列车气动力随透风率的增加而增大，下游列车则基本不变；相对而言，风屏障透风率大小对列车气动特性影响较大，高度影响较小，且二者存在一个最优组合；尽管风屏障会使平均气动力减小，但其产生的特征紊流使得气动力脉动增强，极大气动力可能会增大，风屏障参数应通过风洞试验或数值模拟慎重选取。

[1]何旭辉, 邹云峰, 周佳, 等.运行车辆风环境参数对其气动特性与临界风速的影响[J]. 铁道学报, 2015, 37(5): 1—6.

He Xuhui, Zou Yunfeng, Zhou Jia, et al. Effect of wind environment parameters on aerodynamic characteristics and critical wind velocity of vehicle operation[J]. Journal of the China Railway Society, 2015, 37(5): 1—6.

[2]Baker C J, Cheli F, Orellano A, et al. Cross-wind effects on road and rail vehicles[J]. Journal of Vehicle Mechanics and Mobility, 2009, 47(8):983—1022.

[3]刘庆宽. 强风环境下列车运行安全保障体系的初步研究[J]. 工程力学, 2010, 27(S1):305—310.

Liu Qingkuan. Study on the system to ensure train operation safety under strong wind[J]. Engineering Mechanics, 2010, 27(S1):305—310.

[4]Matschke G, Schulte W B. Measures and strategies to minimise the effect of strong cross winds on high speed trains[C]. The Proceedings of the World Congress of Railway Research, 1997:178—255.

[5]王厚雄, 王蜀东, 高注, 等. 防风工程对风特性及铁道车辆横风气动特性的影响[J]. 空气动力学学报, 1990, 8(4):430—436.

Wang Houxiong, Wang Shudong, Gao Zhu, et al. The effects of wind break engineering on wind characteristics and lateral aerodynamic characteristic of railway cars[J]. Acta Aerodynamic Sinica, 1990, 8(4):430—436.

[6]向活跃. 高速铁路风屏障防风效果及其自身风荷载研究[D]. 成都: 西南交通大学土木工程学院, 2013.

Xiang Huoyue. Protection effect of wind barrier on high speed railway and its wind loads[D]. Chengdu: College of Civil Engineering of Southwest Jiaotong University, 2013.

[7]姜翠香, 梁习锋. 挡风墙高度和设置位置对车辆气动性能的影响[J]. 中国铁道科学, 2006, 27(2):66—70.

Jiang Cuixiang, Liang Xifeng. Effect of the vehicle aerodynamic performance caused by the height and position of wind-break wall[J]. China Railway Science, 2006, 27(2):66—70.

[8]周奇, 朱乐东, 郭震山. 曲线风障对桥面风环境影响的数值模拟[J]. 武汉理工大学学报, 2010, 32(10):38—44.

Zhou Qi, Zhu Ledong, Guo Zhenshan. Numerical simulation for curve windshield barrier effects on wind environment around bridge deck[J]. Journal of Wuhan University of Technology, 2010, 32(10):38—44.

[9]Coleman S A, Baker C J. The reduction of accident risk for high sided road vehicles in cross winds[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1992, 41-44:2685—2695.

[10]Papesch A J G. Model study of windbreaks on railway on bridge[J]. New Zealand Engineering, 1972, 27(4):132—139.

[11]Kwon S D, Kim D H, Lee S H, et al. Design criteria of wind barriers for traffic. Part1: wind barrier performance[J]. Wind and Structures, 2011, 14(1):55—70.

[12]Kim D H, Kwon S D, Lee I K, et al. Design criteria of wind barriers for traffic. Part2: decision making process[J]. Wind and Structures, 2011, 14(1):71—80.

[13]Kozmar H, Procino L, Borsani A, et al. Sheltering efficiency of wind barriers on bridges[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2012, 107-108:274—284.

[14]Suzuki M, Tanemoto K, Maeda T. Aerodynamic characteristics of train/vehicles under cross winds[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2003, 91:209—218.

[15]Cheli F, Corradi R, Rocchi A, et al. Wind tunnel tests on train scale models to investigate the effect of infrastructure scenario[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2010, 98:353—362.

[16]邹云峰. 巨型冷却塔群的风效应及其风洞试验方法研究[D]. 长沙: 湖南大学土木工程学院, 2013.

Zou Yunfeng. Study on wind effects and wind-tunnel test method for super large cooling towers group[D]. Changsha: College of Civil Engineering of Hunan University, 2013.

[17]何旭辉, 邹云峰, 杜风宇. 风屏障对高架桥上列车气动特性影响机理分析[J]. 振动与冲击, 2015, 34(3): 66—71.

He Xuhui, Zou Yunfeng, Du Fengyu. Mechanism analysis of wind barrier's effects on aerodynamic characteristics of a train on viaduct[J]. Journal of Vibration and Shock, 2015, 34(3): 66—71.

[18]李永乐, 向活跃, 廖海黎. 铁路风屏障防风效果的风洞试验研究[C]. 第十六届全国结构风工程学会会议论文集. 成都: 西南交通大学出版社, 2013:227—228.

Li Yongle, Xiang Huoyue, Liao Haili. Wind tunnel test study on windbreak effect of railway wind barrier[C]. The Proceedings of 11thStructural Wind Engineering Conference. Chengdu: Southwest Jiaotong University Press, 2013:227—228.

[19]He X H, Zou Y F, Wang H F, et al. Aerodynamic characteristics of a trailing rail vehicles on viaduct based on still wind tunnel experiments[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2014, 135: 22—33.

Effect of wind barrier on aerodynamic characteristics for the trailing train under cases of vehicle-bridge coupling

ZOUYun-feng1,2,3,HEXu-hui1,2,LIHuan1,2,QINHong-xi1,2,SHIKang1,2,HUANGYong-ming1,2

(1.Department of Bridge Engineering, School of Civil Engineering, Central South University, Changsha 410075, China;2.National Engineering Laboratory for High Speed Railway Construction, Changsha 410075, China;3.China Construction Fifth Engineering Division CORP., LTD, Changsha 410004, China)

Installing wind barrier is one of the effective methods to improve the security of the running train. However, the wind shielding effect is influenced by many factors, such as wind barrier parameters and its surroundings. The models of CRH2 type train and 32m pre-stressed concrete simply supported box beam viaduct at Beijing-Shanghai high-speed rail line are manufactured with geometric scale of 1:25 in order to investigate the effects of wind barrier parameters, namely porosity and height, on aerodynamic forces and pressure distribution of trailing vehicles under representative combination cases of model vehicles on double tracks on the model viaduct. Based on the simultaneous pressure measurement, the aerodynamic forces are obtained by the use of the proper orthogonal decomposition technique, according to which pressure measurement points can be increased. It is shown that when the pressure taps distribution is appropriate and sufficiently dense, the steady aerodynamic forces generated by pressure complementary calculations are as accurate as those by the force test. While the aerodynamics of leeward vehicle is less affected, the effects of wind shield on the windward vehicle are significantly affected by wind barrier. In general, the effect of the porosity of wind barrier on aerodynamic characteristics is greater than that of its height, and there is an optimal combination between wind barrier porosity and height. Although the mean aerodynamic forces of vehicle will be reduced with the installation of wind barrier, the maximum aerodynamic forces may increase because of the effect of the characteristic turbulence. Therefore, wind barrier parameters should be carefully chosen in wind tunnel test or computational fluid dynamics numerical simulation.

high-speed railway; wind barrier; combination of vehicle and bridge; trailing rail vehicle; aerodynamic characteristics; wind tunnel test

2014-04-24；

2015-11-09

国家自然科学基金资助项目(51178471, 51322808, 51508580)；长沙理工大学桥梁工程安全控制省部共建教育部重点实验室开放基金资助项目(14KB02)；中国博士后科学基金资助项目(2014M562133)；中国铁路总公司科技研究开发计划项目(2015G002-C)；中南大学“创新驱动计划”资助项目(2015CX006)

U271.91; U216.9

A

1004-4523(2016)01-0156-10

10.16385/j.cnki.issn.1004-4523.2016.01.020

邹云峰(1984—),男,讲师。电话:13874997131;E-mail:yunfengzou@csu.edu.cn