齿向修形直齿轮系统动力学特性分析*

王奇斌， 张义民

(1.西安电子科技大学机电工程学院， 陕西 西安 710071；2.东北大学机械工程与自动化学院， 辽宁 沈阳 110819)



齿向修形直齿轮系统动力学特性分析*

王奇斌1， 张义民2

(1.西安电子科技大学机电工程学院， 陕西 西安 710071；2.东北大学机械工程与自动化学院， 辽宁 沈阳 110819)

研究了直齿轮齿向修形对齿轮系统振动特性的影响。首先考虑直齿轮齿向修形偏差，将轮齿沿轴向离散成若干宽度相等的薄片，建立了齿轮副啮合刚度模型。然后以一对直齿轮副为例，分别使用有限元法和本文方法分析了齿轮副啮合刚度，结果表明所提方法能够快速准确求解齿向修形直齿轮副的啮合刚度。最后建立齿轮系统有限元模型，分析了齿向修形对系统固有特性、振动响应特性的影响。研究结果表明：齿向修形降低了齿轮副啮合刚度，考虑齿向修形后齿轮系统弯扭耦合固有频率减小，齿轮系统响应的共振峰出现了偏移。研究结果可为齿向修形齿轮的动态响应计算和结构设计提供理论依据。

直齿轮; 齿向修形; 啮合刚度模型; 有限元模型; 振动特性

引　言

齿轮传动系统，包括传动轴、轴承、箱体等零部件，在载荷的作用下将会产生弯曲变形和扭转变形。这些变形将会使轮齿啮合的接触线发生畸变，导致轮齿沿齿宽方向产生边缘接触，造成载荷分布不均匀，出现偏载现象。制造、安装误差会进一步加剧这种现象[1]。因此需要对齿轮齿向修形来补偿制造误差、安装误差和支承变形，从而避免边缘接触、载荷分布不均匀等现象。

直齿轮齿向修形主要是将直齿轮沿齿向修鼓，从而避免边缘接触，防止边缘部位提前损坏而影响齿轮副的工作寿命。齿向修形方式主要有齿向圆弧修形、多项式函数修形、齿端倒圆角等方式。而齿向修形使得齿轮存在齿廓偏差，齿廓偏差对齿轮系统的振动特性有着很大的影响[2-3]。

国内外许多学者针对齿廓偏差对齿轮时变啮合刚度、传递误差以及轮齿接触应力和齿根弯曲应力的影响做了大量的研究工作[4-8]。文献[4-5]将轮齿简化为悬臂梁，考虑齿轮的弯曲刚度、剪切刚度、径向压缩刚度和齿面接触刚度，运用势能法计算轮齿的刚度，最后考虑单双齿交替啮合的影响计算了齿轮副的时变啮合刚度。在前面研究的基础上，Chen等[6-7]考虑齿顶修形和齿根裂纹的影响建立了通用的齿轮副啮合刚度和传递误差计算模型。Li[8]使用有限元法研究了制造误差、安装误差以及齿廓修形对直齿轮齿面接触应力、齿根弯曲应力、载荷分布和传递误差的影响。

而针对齿轮系统动力学，国内外的研究人员也做了大量的工作[9-12]。文献[13]考虑齿轮系统的弯扭耦合振动，建立了齿轮系统弯扭耦合动力学模型，分析了系统的动力学特性。文献[14-15]以直齿轮为例，考虑直齿轮几何偏心，分析了齿轮转子系统的振动响应。在上述文献的基础上，Kubur等[16]以斜齿轮为例，考虑齿轮的弯扭轴摆耦合，建立了齿轮动力学模型，并与转子轴承系统耦合，分析了齿轮转子轴承系统的动力学特性。Zhang等[17]建立了斜齿轮几何偏心动力学模型，分析了几何偏心斜齿轮转子系统动力学特性。王奇斌等[18]考虑斜齿轮齿面啮合刚度分布、传递误差分布，建立了通用的斜齿轮集中质量模型并分析了齿轮转子系统振动特性，该模型具有很好的通用性和较高的精度。

在前述文献的基础上，Abbes等[19]通过有限元法建立了齿基刚度模型，分析了不同的齿基类型对齿轮总刚度的影响和对齿轮系统振动特性的影响。Kaharman等[2]和马辉等[20]均以直齿轮为例，分析了齿轮齿顶修形对齿轮啮合刚度的影响，以及对齿轮系统振动特性的影响，结果显示通过齿轮齿顶修形，能够显著地降低齿轮系统的振动。Velex等[3,20]考虑齿廓误差，分析了直齿轮和斜齿轮啮合刚度和传递误差，以及齿顶短修形和长修形对齿轮啮合刚度和传递误差的影响，最后分析了齿轮系统的振动特性。以上文献考虑齿基刚度、齿廓修形对齿轮啮合刚度、传递误差和系统振动特性的影响，而考虑轮齿齿向修形对齿轮啮合刚度和传递误差的影响，分析齿轮系统动力学特性的文章还不多见。

因此本文考虑齿向修形，建立了齿轮副啮合刚度和传递误差模型。然后以一对直齿轮副为例，分别使用有限元法和本文方法对结果进行对比验证。最后，建立了齿轮系统有限元模型，分析了无齿向修形和有齿向修形的直齿轮系统动力学特性。

1　啮合刚度模型

本节考虑齿轮齿向修形，建立齿轮啮合刚度和传递误差模型。

1.1齿向修形直齿轮啮合刚度模型的建立

对于理想齿廓的直齿轮副，齿轮副的啮合刚度等于同时参与啮合的各轮齿对啮合刚度之和，而对于存在齿廓偏差的轮齿，应用该方法计算齿轮副的啮合刚度存在着很大的误差。本节建立齿向修形齿轮副啮合刚度模型。将齿向修形的齿轮沿齿宽方向离散成若干宽度相等的薄片，如图1所示。每一个薄片都被视为直齿轮，那么直齿轮副啮合等同于由若干对薄片轮齿对组成的啮合副。

图1　轮齿薄片模型Fig.1　Discrete model of a tooth

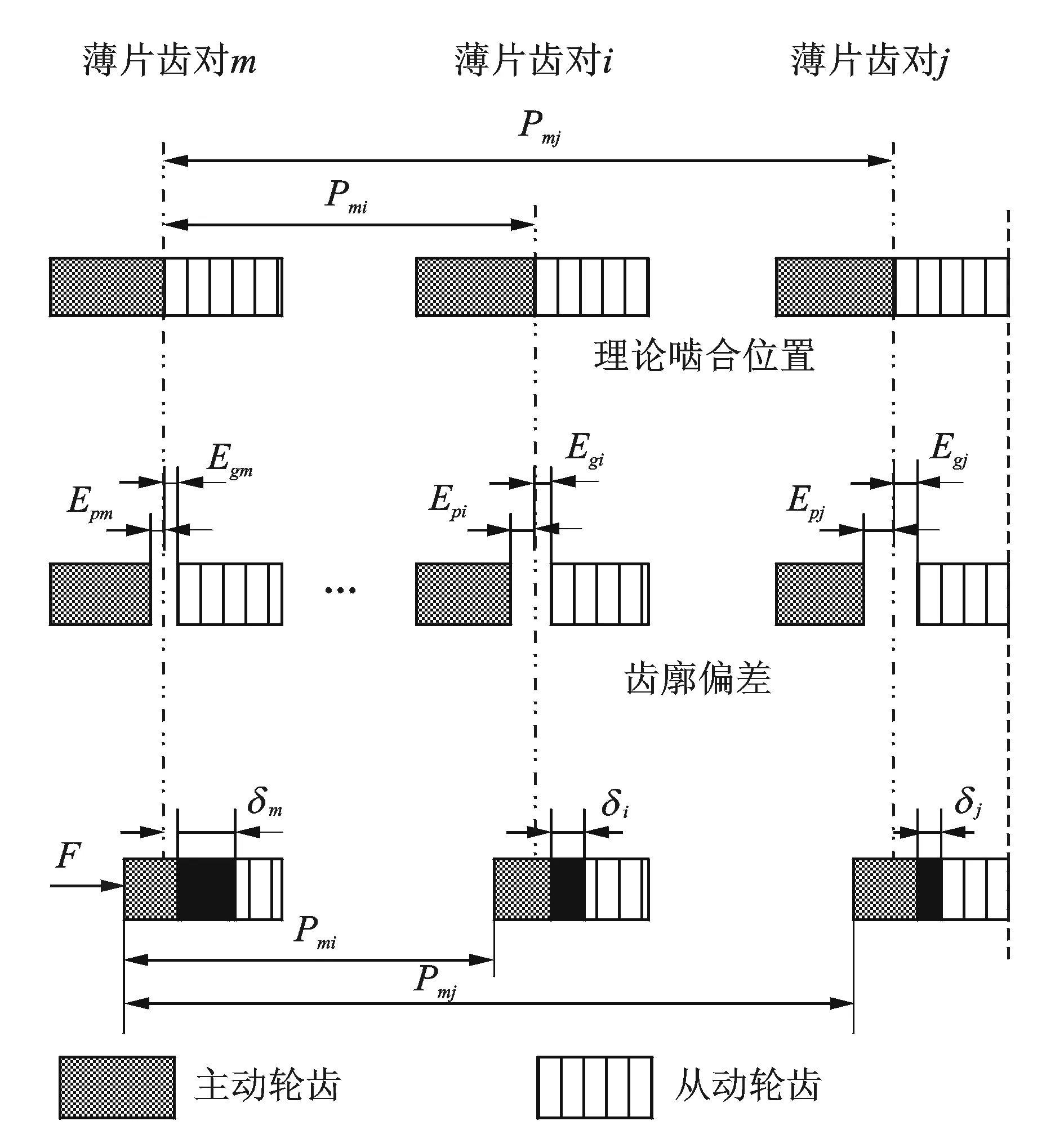
图2　各薄片轮齿相对位置关系Fig.2　Relative position relationships of sliced teeth with tooth profile errors

理想齿廓时，各对轮齿同时在理论啮合位置接触，当齿轮存在齿向修形时，各薄片轮齿对存在齿廓偏差，这些薄片轮齿对相对位置关系如图2所示。Pmi，Pmj为各薄片轮齿对沿啮合线方向上的理论相对距离。Eni为各薄片轮齿实际齿廓偏离理论位置的距离，其中n=p代表主动齿轮，n=g代表从动齿轮，i为各对轮齿的编号。i=m代表该时刻下参与啮合的薄片轮齿对中齿廓偏差最小的薄片轮齿对，即Epm+Egm=min(Epi+Egi)。啮合过程中存在齿廓偏差的薄片轮齿对在外载荷力的作用下，主动齿轮转动，轮齿转过由齿廓偏差引起的间隙，齿廓偏差小的薄片轮齿对先发生接触并发生变形；在外力的持续作用下主动齿轮继续转动，齿轮变形量也继续增大，当齿轮变形量δm大于薄片轮齿对齿廓偏差(Epi+Egi)时，该薄片轮齿对相互接触并发生变形。直到各薄片轮齿对变形的反推力之和等于外载荷力。此时相互啮合的各轮齿对之间的几何关系如下：

(1)

式中δm，δi和δj分别为各轮齿对在外载荷力作用下的变形量。式(1)可变化为：

(2)

根据胡克定律，处于啮合状态的轮齿，其刚度ki与变形量δi有如下的关系

(3)

式中ki为各薄片轮齿对的啮合刚度，其计算方法可参考文献[8]中直齿轮的刚度计算方法。由于齿向修形量非常小(微米级)，所以认为这些修形误差对单个薄片轮齿刚度的影响可以忽略[22]。且认为这些微小的修形不改变轮齿的理论啮合线。本文中当该对轮齿在外力的作用下没有接触上，即δi≤0时，令ki=0。

(4)

总啮合力等于参与啮合的各轮齿对的啮合力之和。

(5)

式中N等于同时参与啮合的薄片轮齿对数。那么轮齿啮合的总刚度等于外载荷力除以轮齿的最大变形量，即

(6)

联合式(2)～(6)，求得该啮合状态下齿轮最大变形量和齿轮副啮合总刚度为：

(7)

(8)

式中j=m时，Emj=0。齿轮副在该啮合状态下的无载荷传递误差(NLTE)为

(9)

齿轮副该啮合状态下载荷传递误差(LSTE)为

(10)

1.2齿向修形直齿轮齿廓偏差计算

直齿轮齿向修形主要有圆弧修形、多项式函数修形等修形曲线[1,23-25]。为了方便起见，本文采用齿向圆弧修形曲线。如图3所示，细实线代表理想齿廓，粗实线代表齿向修形后的齿廓。根据几何关系，薄片轮齿的齿廓偏差为

(11)

图3　齿向修形示意图Fig.3　Tooth lead crown relief

式中b为薄片沿齿宽方向上的坐标。R为修形圆弧半径，R的大小取决于修形量Cβ和齿宽B。

(12)

根据1.1节和1.2节中的理论，考虑齿向修形偏差，运用Matlab建立了齿轮副啮合刚度求解程序。在本文的计算中，取每个薄片轮齿的宽度Δl=0.5 mm。啮合刚度的计算过程如图4所示。

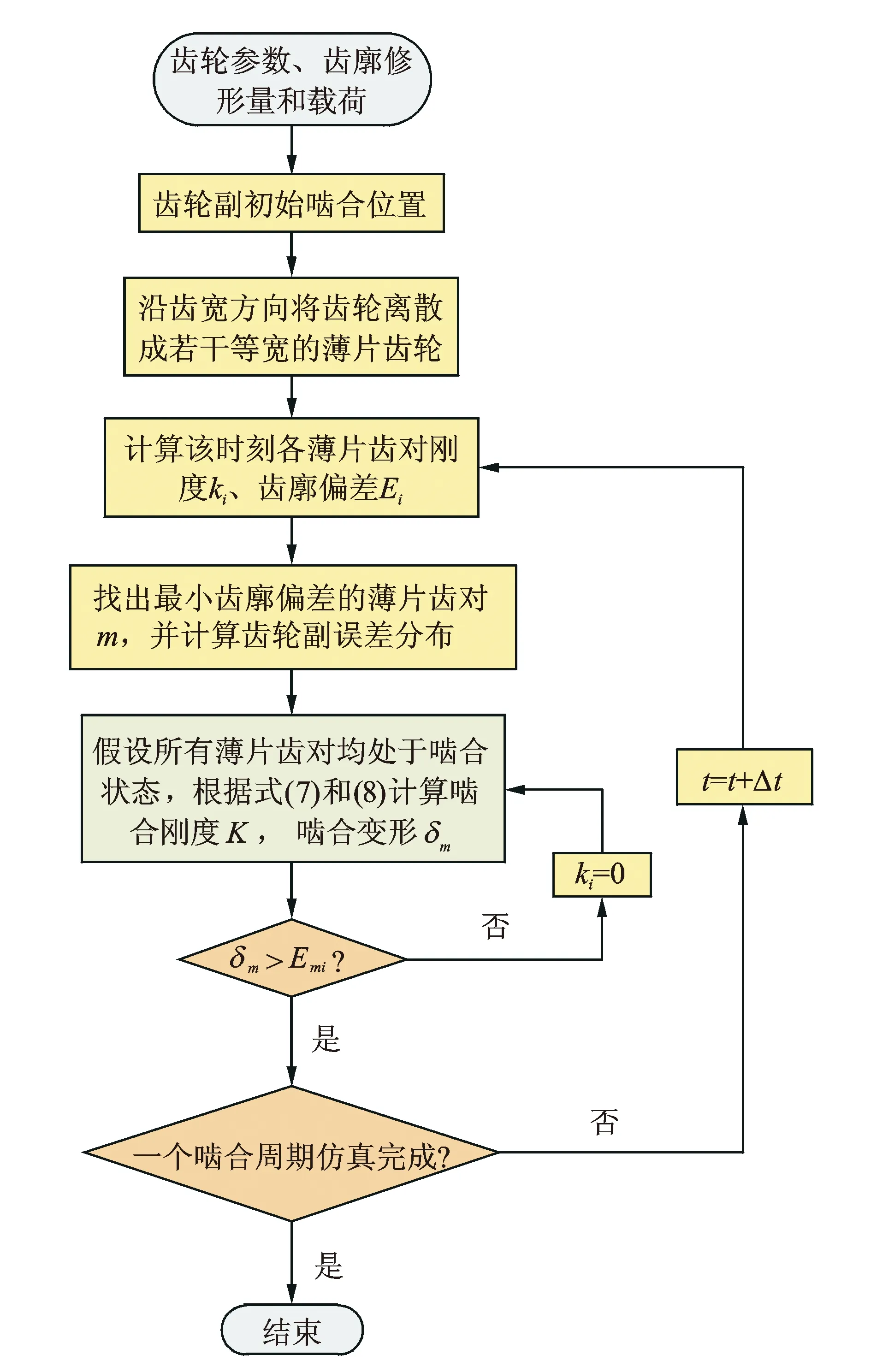
图4　齿轮啮合刚度计算流程图Fig.4　Flow chart of the mesh stiffness calculation for a gear pair with lead crown relief

1.3模型验证

本节以表1中的直齿轮参数为例，分别使用本文方法和有限元方法分析无齿向修形和齿向修形Cβ=20 μm两种情况下齿轮副的啮合刚度。采用有限元分析软件ANSYS建立齿轮的有限元模型，如图5所示，分别在无修形和有齿向修形情况下对齿轮副进行接触分析。图6为两种情况下齿轮的接触应力图。从图中可以看出，在无齿向修形时，轮齿接触区域沿整个齿宽方向上均布，而存在齿向修形时，轮齿接触区域分布于齿宽中间部分，即齿廓偏差比较小的部分。分别使用两种方法，齿轮啮合刚度计算结果如图7所示。从图中可以看出，在不存在齿向修形时，运用本文方法求解的啮合刚度略大于有限元方法求解的啮合刚度，最大相对误差为4.7%。

表1　齿轮参数

考虑齿向修形Cβ=20 μm时，齿轮副的啮合刚度均大幅度降低，运用本文方法降低了48.8%，而运用有限元方法降低了43.8%，此时，两种方法的最大相对误差为4.8%。运用本文方法每个啮合周期分析50个点使用普通个人电脑约耗时3 min，运用有限元方法每个啮合周期分析12个点使用普通个人电脑约耗时6 h。所以运用本文的分析方法能够快速准确的计算出存在齿向修形的齿轮副啮合刚度。

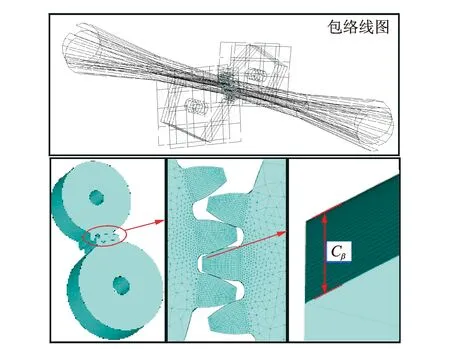
图5　齿轮有限元模型Fig.5　Finite element model of the gear pair

图6　齿廓接触区域图Fig.6　Contact pattern under different lead crown reliefs

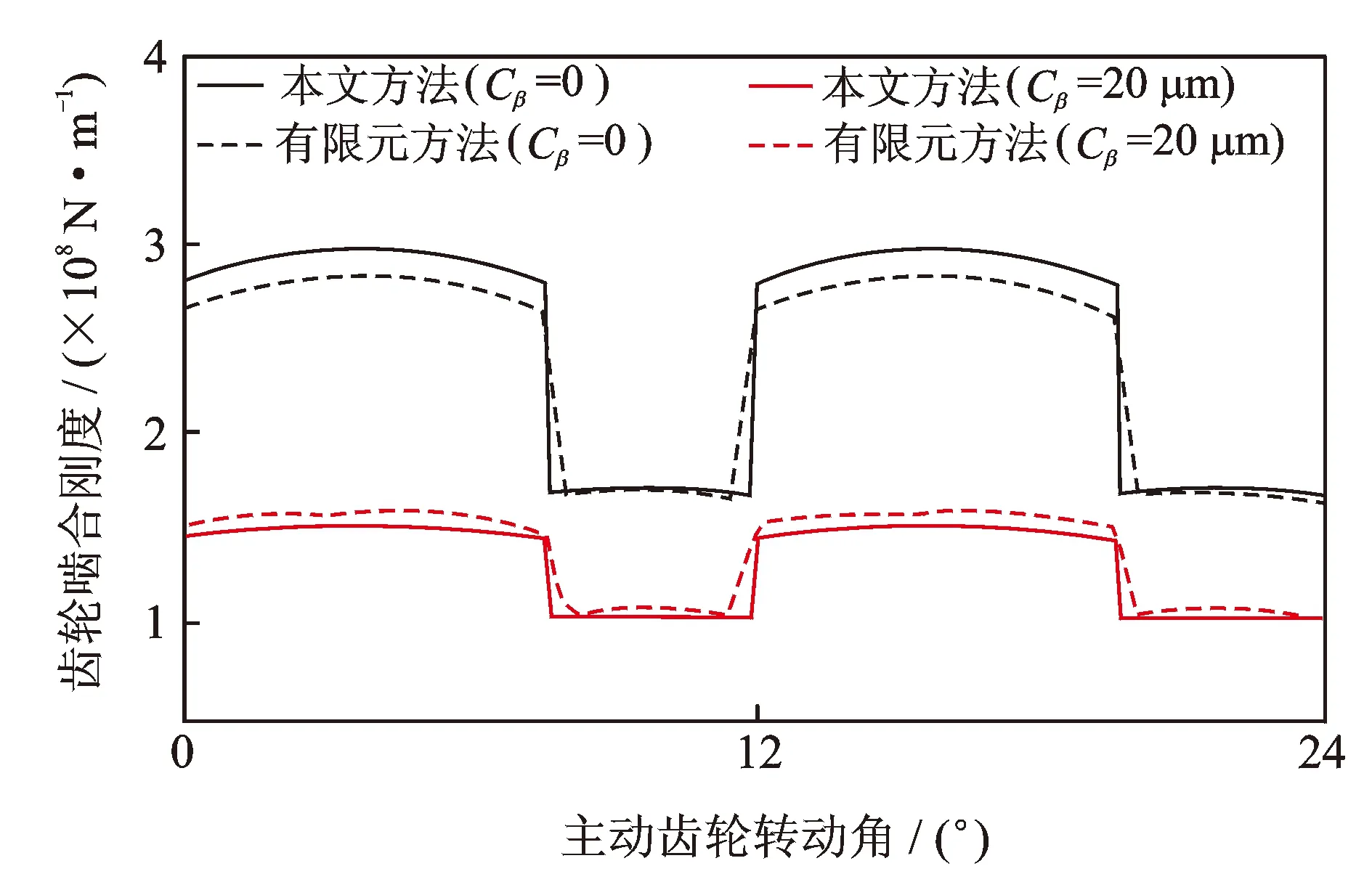
图7　齿轮啮合刚度对比图Fig.7　Mesh stiffness comparison of the proposed method and the finite element method

2　齿轮系统有限元模型

齿轮系统如图8所示，该系统由齿轮、轴和轴承组成，其中齿轮啮合模型采用作者已发表的12自由度通用齿轮弯扭轴摆耦合动力学模型[17]，该模型综合考虑了齿轮安装角、螺旋角、压力角、齿轮转向等因素的影响。对于直齿轮令螺旋角βij=0°，得到直齿轮副啮合模型如下

(13)

式中Mij为齿轮副质量矩阵，Kij为齿轮副啮合刚度矩阵，Fij和Fw分别为由传递误差引起的力向量和外载荷力向量，详细的矩阵形式可参考文献[17]。Xij为齿轮副的广义坐标

(14)

式中x，y为横向自由度；z为轴向自由度；θx，θy为摆动自由度；θz为扭转自由度。在直齿轮系统中，由于没有轴向力和绕x，y方向的扭转力矩，所以令z，θx和θy项为0。

为了计算方便，不考虑阻尼，轴和轴承简化为弹簧单元来模拟，采用4个方向的刚度来模拟其支承作用，如图8所示。

图8　齿轮系统模型Fig.8　Model of the gear-bearing system

根据有限元理论，建立齿轮系统的运动方程如下

(15)

式中M，C，G和K分别为系统质量、阻尼、陀螺和刚度矩阵。u为系统广义坐标，Fu为外激励向量。其中阻尼矩阵C采用瑞利阻尼来确定，其表达式如下

(16)

式中α，β为质量矩阵和刚度矩阵比例系数，计算方法可参考文献[17]。

3　系统振动特性分析

本节以表1中的齿轮参数和表2中轴和轴承刚度参数为例，考虑齿向修形的影响，建立齿轮啮合刚度、传递误差模型，分析齿轮时变啮合刚度和无载荷传递误差，然后结合齿轮系统有限元模型，分析齿轮系统的动力学特性。

表2　刚度参数

本节分别分析了无齿向修形和齿向修形量Cβ=20 μm时齿轮的时变啮合刚度和无载荷传递误差，如图9所示。从图9(a)中可以看出，齿向修形使得齿轮的啮合刚度大幅度减小，齿向修形量Cβ=20 μm时齿轮副啮合刚度的最大值相比齿向不修形时降低了48.8%。在图9(b)中，两种情况下，无载荷传递误差始终为0，说明齿向修形对无载荷传递误差没有影响，齿向修形没有改变齿轮的理论啮合位置。

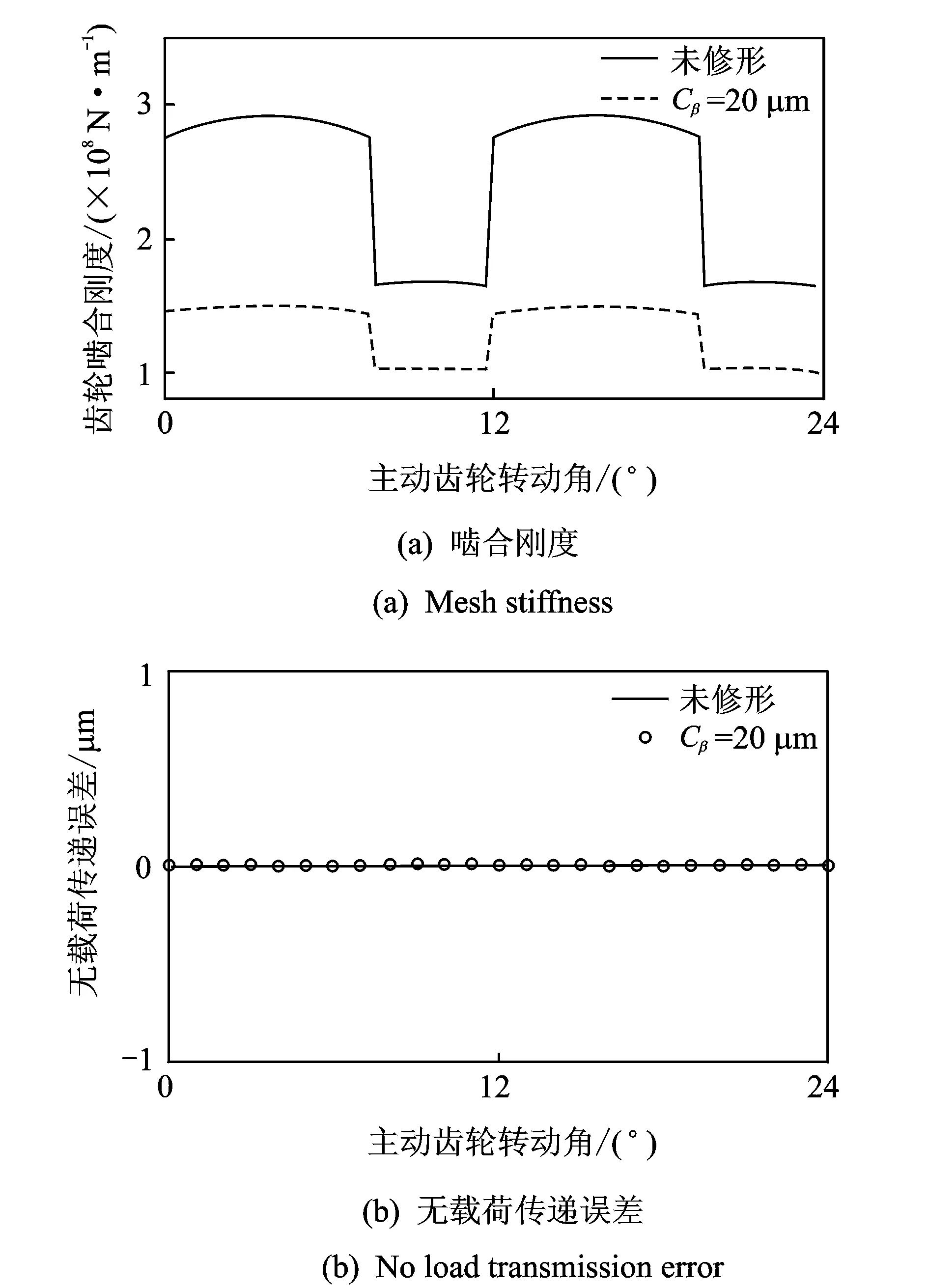
图9　不同修形量结果对比Fig.9　Comparison of the results

在无齿向修形和齿向修形Cβ=20 μm两种情况下，使用齿轮平均啮合刚度对齿轮系统固有特性分析，结果如表3所示。从表中可以看出，齿向修形只对齿轮系统弯扭耦合固有频率有影响，相比无齿向修形，齿向修形Cβ=20 μm时系统第1阶固有频率下降了约8%。所以在齿轮系统固有特性分析中，应该考虑齿向修形的影响。

在无齿向修形和齿向修形Cβ=20 μm两种情况下，对齿轮系统振动特性进行分析，结果如图10所示。图10(a)，(b)分别为无齿向修形和有齿向修形两种情况下主动齿轮处x，θz方向的振动响应图。图10(a)，(b)中都出现了一些共振峰值，将这些峰值与系统固有频率进行对比，结果显示这些峰值均是由齿轮副的啮合频率等于系统的第1阶固有频率ω1及其谐波项ω1/2，ω1/4和ω1/8引起的。而相比无齿向修形，在齿向修形Cβ=20 μm时，系统的共振峰值均出现了偏移，且x方向振动峰值变小。这是因为齿向修形使得齿轮副啮合刚度减小，从而系统第1阶固有频率变小，由第1阶固有频率及其谐波项产生的共振峰值出现了偏移。

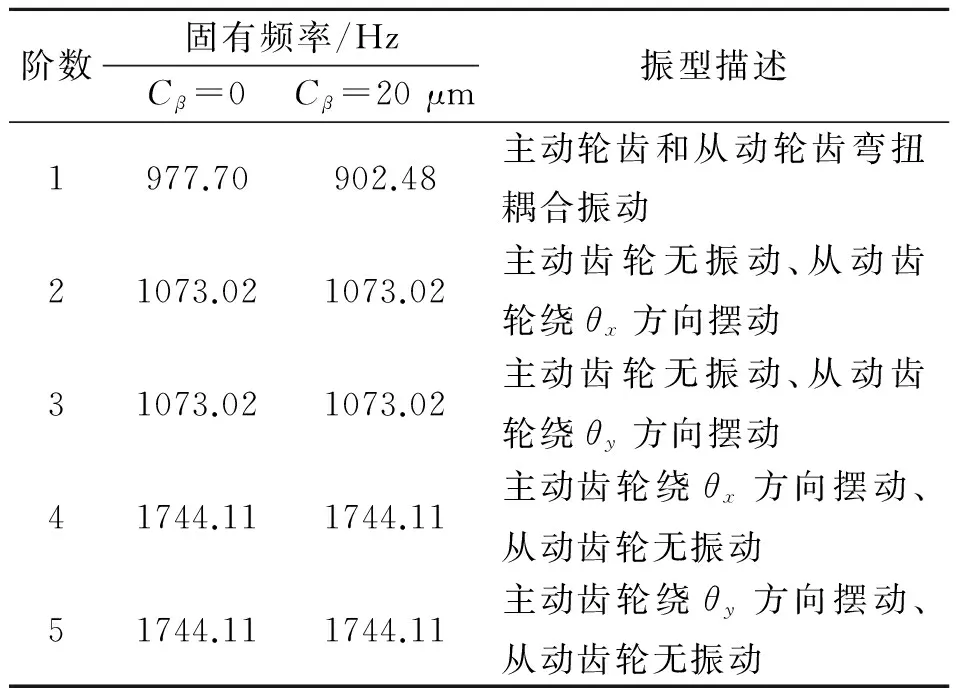
表3　齿轮系统固有频率

总之，齿向修形对齿轮系统的动力学特性有着较大的影响，在齿轮系统动力学特性分析中，应考虑齿向修性的影响。

4　结　论

(1) 考虑直齿轮齿向修形，将轮齿沿轴向离散成若干宽度相等的薄片，建立了齿轮啮合刚度模型。并以一对齿向修形的直齿轮为例，通过有限元方法和本文的方法对结果进行了验证，结果表明本文方法能够快速准确的求解齿向修形直齿轮的啮合刚度。

(2) 建立了齿轮系统有限元模型，分析了系统的固有特性、振动响应及其频谱。结果显示齿向修形降低了齿轮副啮合刚度，考虑齿向修形后齿轮系统弯扭耦合固有频率减小，相比无齿向修形，齿向修形Cβ=20 μm时系统第1阶固有频率下降了约8%。考虑齿向修形后齿轮系统响应图中共振峰出现了偏移，响应中共振峰主要由系统第1阶固有频率和其谐波项组成。

[1]International Organization for Standardization. ISO6336-1—2006, Calculation of load capacity of spur and helical gears-part 1: basic principles, introduction and general influence factors[S]. Geneva, Switzerland, 2006.

[2]Kahraman A, Blankenship G W. Effect of involute tip relief on dynamic response of spur gear pairs[J]. Journal of Mechanical Design, 1999, 121(2): 313—315.

[3]Velex P, Maatar M. A mathematical model for analyzing the influence of shape deviations and mounting errors on gear dynamic behaviour[J]. Journal of Sound and Vibration, 1996, 191(5): 629—660.

[4]Tian X. Dynamic simulation for system response of gearbox including localized gear faults[D]. Alberta, Canada: University of Alberta Edmonton, 2004.

[5]Chaari F, Fakhfakh T, Haddar M. Analytical modelling of spur gear tooth crack and influence on gear mesh stiffness[J]. European Journal of Mechanics a-Solids, 2009, 28(3): 461—468.

[6]Chen Z, Shao Y. Mesh stiffness calculation of a spur gear pair with tooth profile modification and tooth root crack[J]. Mechanism and Machine Theory, 2013, 62: 63—74.

[7]Chen Z, Shao Y. Dynamic simulation of spur gear with tooth root crack propagating along tooth width and crack depth[J]. Engineering Failure Analysis, 2011, 18(8): 2149—2164.

[8]Li S. Effects of machining errors, assembly errors and tooth modifications on loading capacity, load-sharing ratio and transmission error of a pair of spur gears[J]. Mechanism and Machine Theory, 2007, 42(6): 698—726.

[9]王建军, 李其汉, 李润方. 齿轮系统非线性振动研究进展[J]. 力学进展, 2005, 35(1): 37—51.

WANG Jianjun, LI Qihan, LI Runfang. Research advances for nonlinear vibration of gear transmission systems[J]. Advances in Mechanics, 2005, 35(1): 37—51.

[10]Velex P. On the modelling of spur and helical gear dynamic behaviour[J]. arXiv preprint arXiv, 2012, 1204(2636): 75—106.

[11]Wang S, Huo M, Zhang C, et al. Effect of mesh phase on wave vibration of spur planetary ring gear[J]. Europe Journal of Mechanics-A/Solids, 2011, 30: 820—827.

[12]Zhang D, Wang S, Liu J. Parametric vibration of split gears induced by time-varying mesh stiffness[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science 2015,229(1):18—25.

[13]Kahraman A, Ozguven H N, Houser D R, et al. Dynamic analysis of geared rotors by finite elements[J]. Journal of Mechanical Design, 1992, 114(3): 507—514.

[14]Lee A S, HA J W. Prediction of maximum unbalance responses of a gear-coupled two-shaft rotor-bearing system[J]. Journal of Sound and Vibration, 2005, 283(3): 507—523.

[15]蒋庆磊, 吴大转, 谭善光, 等. 齿轮传动多转子耦合系统振动特性研究[J]. 振动工程学报, 2010, 23(3): 254—259.

JIANG Qinglei, WU Dazhuan, TAN Shanguang, et al. Development and application of a model for coupling geared rotors system[J]. Journal of Vibration Engineering, 2010, 23(3): 254—259.

[16]Kubur M, Kahraman A, Zini D M, et al. Dynamic analysis of a multi-shaft helical gear transmission by finite elements: model and experiment[J]. Journal of Vibration and Acoustics, Transactions of the ASME, 2004, 126(3): 398—406.

[17]Zhang Y, Wang Q, Ma H, et al. Dynamic analysis of three-dimensional helical geared rotor system with geometric eccentricity[J]. Journal of Mechanical Science and Technology, 2013, 27(11): 3231—3242.

[18]王奇斌, 胡鹏, 张义民, 等. 基于积分模型的斜齿轮转子系统振动特性分析[J]. 东北大学学报(自然科学版), 2014, 35(05): 721—725.

WANG Qibin, HU Peng, ZHANG Yimin, et al. Vibration characteristics analysis of helical gear rotor systems using the integral model[J]. Journal of Northeastern University (Natural Science), 2014, 35(5): 721—725.

[19]Abbes M S, Trigui M, Chaari F, et al. Dynamic behaviour modelling of a flexible gear system by the elastic foundation theory in presence of defects[J]. European Journal of Mechanics-A/Solids, 2010, 29(5): 887—896.

[20]马辉, 逄旭, 宋溶泽, 等. 考虑齿顶修缘的齿轮-转子系统振动响应分析[J]. 机械工程学报, 2014, 50(7): 39—45.

MA Hui, PANG Xu, SONG Rongze, et al. Vibration response analysis of a geared rotor system considering the tip relief[J]. Journal of Mechanical Engineering, 2014, 50(7): 39—45.

[21]Velex P, Ajmi M. On the modelling of excitations in geared systems by transmission errors[J]. Journal of Sound and Vibration, 2006, 290(3): 882—909.

[22]Liu G, Parker R G. Dynamic modeling and analysis of tooth profile modification for multimesh Gear vibration[J]. Journal of Mechanical Design, 2008, 130(12): 1—13.

[23]Eritenel T, Parker R G. An investigation of tooth mesh nonlinearity and partial contact loss in gear pairs using a lumped-parameter model[J]. Mechanism and Machine Theory, 2012, 56: 28—51.

[24]Mohamad E N, Komori M, Murakami H, et al. Analysis of general characteristics of transmission error of gears with convex modification of tooth flank form considering elastic deformation under load[J]. Journal of Mechanical Design, 2009, 131(6): 1—9.

[25]尚振国.风力发电机增速器齿轮修形技术研究[D]. 大连: 大连理工大学, 2010.

Shang Zhenguo. Research on gear modification of speed increasing gearboxes for wind turbines[D]. Dalian:Dalian University of Techndogy,2010.

Dynamic characteristics analysis of a spur gear system with the lead crown relief

WANGQi-bin1,ZHANGYi-min2

(1.School of Electro-Mechanical Engineering, Xidian University, Xi′an 710071, China;2. School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China)

The present work is intended to analyze the vibration characteristics of a gear system with the lead crown relief. A model is introduced for analyzing the influence of the lead crown relief on the gear meshing stiffness. The tooth is approximated as a series of independent spur gear slices along axial direction whose face-width is relatively small. Then the meshing stiffness is calculated by the finite element method and the proposed method for comparison. It is demonstrated that the proposed method is fast and accurate to calculate the gear meshing stiffness with the lead crown relief. Finally, the vibration characteristics of a gear system are analyzed. The results show that the meshing stiffness and the natural frequencies of the flexural and torsional vibrations become smaller for the tooth with lead crown relief. The frequencies where the resonances occur also become smaller with the lead crown relief.

spur gear; lead crown relief; meshing stiffness model; finite element model; vibration characteristics

2014-08-28；

2015-03-31

国家自然科学基金资助项目(51135003)；国家重点基础研究发展计划(973计划)(2014CB046303)和中央高校基本科研业务费专项资金资助项目(N130603002)

TH113.1;TH132.41

A

1004-4523(2016)01-0061-08

10.16385/j.cnki.issn.1004-4523.2016.01.009

王奇斌(1988—)，男，博士,讲师。电话： (029)88203115; E-mail: qbwangpap@163.com