热耗散变形下干气密封系统轴向振动稳定性分析*

丁雪兴， 陆俊杰， 刘　勇， 张英杰

(兰州理工大学石油化工学院， 甘肃 兰州 730050)



热耗散变形下干气密封系统轴向振动稳定性分析*

丁雪兴， 陆俊杰， 刘勇， 张英杰

(兰州理工大学石油化工学院， 甘肃 兰州 730050)

基于非线性振动理论，建立了气膜-密封环系统轴向振动模型，同时考虑了热耗散有热弹变形对气膜厚度和刚度的影响。在特定的工况下，求解并拟合了非线性气膜的轴向刚度和阻尼，获得了一个非线性受迫振动微分方程。在无外激励情况下，通过求解Floquet指数，讨论了系统分岔的问题，分析了螺旋角对系统稳定性的影响，得到了干气密封系统稳定运行的螺旋角范围，并求得螺旋角为75°54′36″时系统发生Hopf分岔。将数据结果与无热耗散有热弹变形、无变形下的数据进行比较。研究结果表明:考虑热耗散有热弹变形下的系统稳定的螺旋角范围比无热耗散有热弹变形和无变形的螺旋角范围更大。热耗散热弹变形下发生Hopf分岔的分叉点位置相比无热耗散有热弹变形和无变形的分岔点更加突出。这与先前利用龙格-库塔法研究的结果一致，从而验证该方法的正确性。其结果说明，热耗散有热弹变形对干气密封系统的稳定运行有一定的干扰，对工程实际具有一定应用价值。

非线性振动； 干气密封; 热耗散； 分岔； 稳定性

引　言

在高速透平机械、泵、反应釜等设备的轴端密封中，干气密封内部气膜平衡间隙[1-2]为微米级尺度。若间隙发生微小变化，极有可能导致干摩擦和泄漏量增大。从而保证气膜-密封环动态稳定性是干气密封可靠运行的关键。因此针对干气密封系统稳定性的分析，一直是国内外研究的热点和难点。

Zirkelback[3],Miller[4]等分别采用有限元法、半解析法求解雷诺方程，获得了气膜特性规律。Zhang[5]建立了3个自由度的微扰运动方程，并用正交分解法求得了密封环三维运动规律。刘雨川[6]利用有限元法，获得了有关密封气膜稳定性的判据。杜兆年等[7-8]用微扰法、近似解析法对轴向振动和角向涡动下，部分气膜动态特性参数进行了计算。张伟政等[9]利用龙格-库塔法求解了轴向振动方程，分析了螺旋角和槽深对振动位移的影响。俞树荣[10]针对气膜-密封环系统轴向振动，探究了系统的稳定性。但是基于非线性振动理论，考虑热耗散变形下气膜-密封环流固耦合系统动态稳定性的影响未做深入研究，由于静环发生变形，气膜厚度结构将产生变化，导致动静环碰摩，最终引起密封失效。

本文基于非线性振动理论和微尺度内热耗散变形，研究干气密封气膜-密封环系统轴向振动的稳定性问题，探求干气密封稳定运行的结构参数区域，并与无耗散有变形、无变形的结构参数区域进行比较，从而分析干气密封运行的稳定性和指导干气密封的优化设计。

1　模型与基本方程的建立

1.1干气密封工作原理和结构

干气密封结构主要由加载弹簧、O 形圈、静环和动环组成，如图1所示。动环依靠轴套固定在旋转轴上并随轴旋转。缓冲气体注入到密封装置，动、静环在流体静压力和弹簧力的作用下保持贴合，起到密封作用。当动环旋转时，将把密封气体周向吸入槽内，气体沿槽向槽根部运动，逐渐被压缩，如图2所示。密封堰是开槽区和非开槽区之间的一个边界，台代表两个开槽区之间的非开槽区域。Ro为密封环的外半径，Ri为密封环的内半径，Rg为密封环的根半径，α为螺旋角，β为螺旋角的余角，r为极半径，φ为极角。当压力达到一定数值时，静环将从动环表面被推开，这样密封面之间始终保持一层极薄的气膜(厚度3～6 μm)。

图1　螺旋槽干气密封结构Fig.1　The structure of spiral groove dry gas seal

图2　密封动环螺旋槽结构Fig.2　The structure of spiral groove of dynamic ring

1.2气膜-密封环系统轴向振动计算模型

模型的假设：

(1)将气膜-密封环系统视为双自由度受迫振动。

(2)气膜假定为具有非线性刚度的弹簧。

(3)瞬态激振力来源于转轴对系统的干扰力，假定为简谐激振力。

(4)动环随轴转动，其轴向位移可假定为简谐运动。

气膜-密封环系统轴向振动模型如图3所示。

图3　气膜-密封环系统轴向振动模型Fig.3　The model of axial vibration of gas film-ring system

振动方程

Kgbcosωt-Cgbωsinωt

(1)

式中m为静环的质量，Ke为弹簧刚度，Kg气膜刚度，Cg为气膜阻尼，x为静环振动位移,xd为动环振动位移，b为动环振幅,ω为轴向振动频率。

2　气膜能量方程及热弹变形

2.1干气密封气膜的能量方程

图4为气膜微元控制体热平衡分析模型。稳态下，由对流换热过程控制方程组[11]推导气膜的能量方程。针对图示的微元控制体，能量的变化分为径向(dr)，环向(dθ)和膜厚方向(dz)。由于控制体随着轴旋转，所以考虑到转速的原因，可以忽略环向(dθ)的温度变化。因此，研究微元以扩散和对流的形式进出控制体的径向能量变化(dr)。

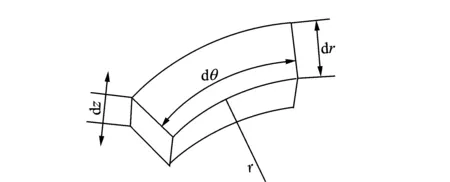
图4　气膜微元控制体热平衡模型Fig.4　The heat balance model for a micro control element of the gas film

则微元体在单位时间内由扩散所吸收的热量为

(2)

单位时间内控制体由对流作用得到的热量为

(3)

在膜厚方向(dz)由于膜厚间隙相当小，因此膜厚方向(dz)的能量主要以扩散形式进出控制体，对流可以忽略。

则微元体在膜厚方向(dz)，在单位时间内由扩散所吸收的热量为

(4)

根据能量守恒定理，再考虑由于流体黏性耗散作用所产生的热量[12]，则能得到螺旋槽干气密封气膜的能量方程

(5)

忽略温度在气膜厚度z方向变化,则气膜的能量方程式(5)简化为

(6)

忽略耗散项，得到不考虑热耗散下的气膜能量微分方程

(7)

2.2干气密封密封环热弹变形

考虑到干气密封的动环材料为合金钢，静环材料为石墨，因此相对于静环的变形量动环变形可忽略。因此干气密封静环轴向热弹变形为[12]

(8)

式中a为材料的线膨胀系数,bf为密封面宽度,L为环的轴向长度；CR=ΔT/bf为温度梯度。

3　干气密封气膜厚度计算

干气密封运转下静环在没有热弹变形时，密封端面间的气膜厚度hb为定值，当有热弹变形时气膜厚度hb为变量，其表达式为

(9)

式中δmax为静环变形量的最大值,hmin为气膜厚度的最小值。hb，hmin，Δ，δmax与δ之间几何关系如图5所示。

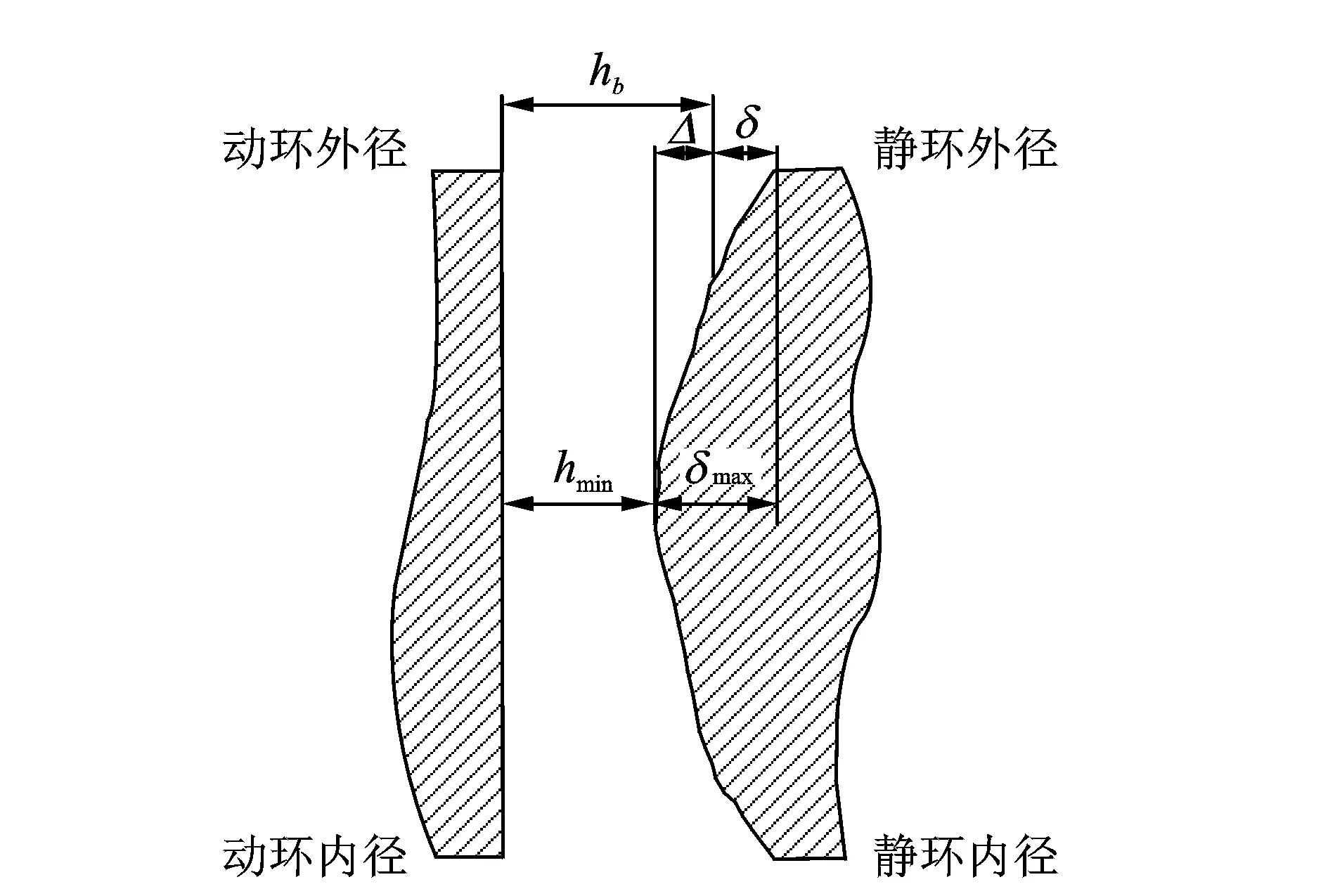
图5　气膜厚度结构简图Fig.5　The structural diagram for the gas film thickness

首先，应用PH线性化方法令非线性偏微分雷诺方程线性化；其次，在求解线性偏微分方程的过程中引入复函数分离变量法，将方程变为两个线性实常数微分方程组。采用迭代法近似求解雷诺方程[13-14]，得气膜推力表达式

(10)

静环发生热弹变形后，由于气膜厚度发生了改变，从而使气膜间进入了另一个新的平衡状态，此时的气膜推力Fo等于闭合力Fc。气膜推力等于静环背侧面介质压力与弹簧力Fe的合力。因此，可得

Fo=p0·A+Fe

(11)

式中A为静环背侧面的面积(m2),Fe为弹簧力(N)。联立式(10)和(11)，利用Maple软件编程，可以求出静密封环受力力平衡时气膜的最小厚度hmin。

4　非线性气膜动态特性参数

4.1气膜非线性刚度Kg和阻尼Cg

应用变分法和PH线性化方法(非线性雷诺方程进行无量纲化,随后对非线性雷诺方程进行PH线性化方法，得到一级近似PH线性雷诺方程。在润滑层中压强小的变化可用其变分ΔP描述，对其方程作变分运算。对变分后的运算公式在稳态边值问题条件下，引入复函数进行化简)运算干气密封螺旋槽内瞬态微尺度流动场的非线性雷诺方程，得到无量纲气膜角向涡动刚度的解析式[8]

(12)

应用PH线性化方法及变分运算，得到了轴向微扰下气膜反作用力的增量。随后再利用复数转换和迭代法对静态下气膜边值问题进行求解，求得气膜轴向刚度的近似解析解。

由于定义的微扰量为复数[7]

(13)

所以稳态下Reynolds方程的微扰动态压力也是复变量[15]，其实部和虚部分别对应于气膜的刚度和阻尼。由微扰动态压力的复数实部Re{K}=η(η1cosω+η2sinω)得到无量纲轴向气膜刚度的计算式，由微扰动态压力的复数虚部Im{K}=η·(-η1sinω+η2cosω)推得无量纲轴向气膜阻尼的计算式。

无量纲气膜轴向刚度[7]、轴向阻尼

(14)

(15)

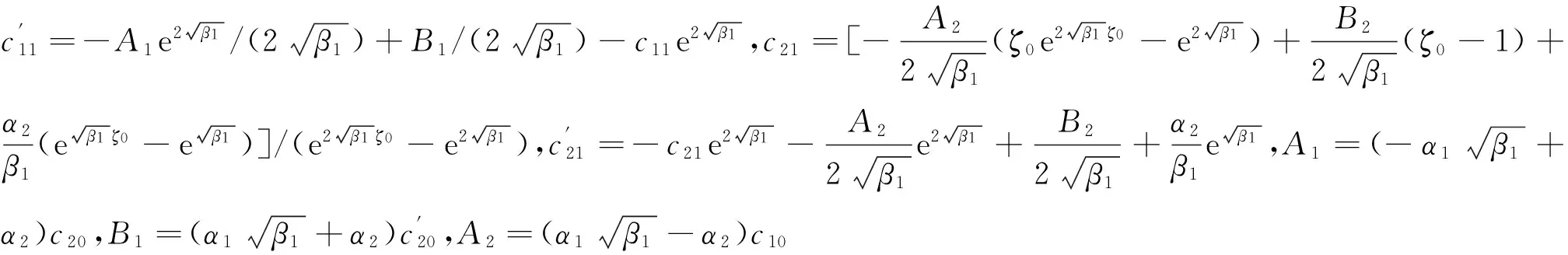
由此，气膜刚度[7,16]：

(16)

气膜阻尼：

(17)

4.2实例计算

样机尺寸：内半径Ri=70.6 mm，外半径Ro=90.25 mm，根半径Rg=80.5 mm，螺旋槽数目n=12，槽深2E=6 μm，螺旋角α=74°51″。

实验工艺参数：介质压力p0=10 MPa，环境压力pi=101.3 kPa，介质气体N2，转速nr=8700 r/min，气膜厚度h=4 μm，静环质量m=0.0804 kg，动环振幅b=10 μm。

联立式(10)和(11)，并且利用Maple求解，得到气膜的最小厚度为3.82 μm。计算过程中，利用迭代法和有限元的思想将非线性的气膜厚度进行逐段计算，最后对式(14)和(15)积分，再代入式(16)和(17)计算后分别得到含有气膜非线性刚度和气膜非线性阻尼的两个多项式。在多项式的常数项和各个系数中将包含了干气密封的结构参数(如螺旋角等)，而螺旋角的变化直接影响螺旋槽干气密封系统的稳定运行。所以通过拟合的办法，对振动敏感参数螺旋角作为变量来研究分岔问题，将其他结构参数作为已知量。最后经过计算得到了拟合后的气膜非线性刚度和气膜非线性阻尼。

拟合气膜非线性刚度

(18)

拟合气膜非线性阻尼

(19)

由轴向追随性可优化出弹簧刚度[17](去追随性系数等于0.4)

Ke=0.4186134080×107

(20)

4.3方程化简

将式(18),(19)代入式(1)中，两边同除以m得

x″+c0x′+c1x+c2x2+c3x3=

(21)

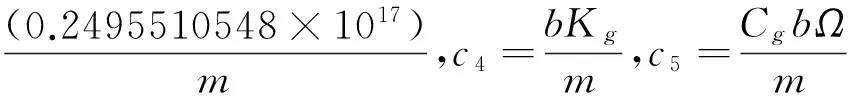
则方程变为

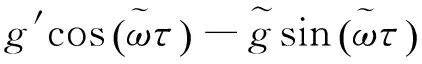
(22)

简化得

(23)

4.4一类非线性动力系统自由振动方程的解

对式(21)的修改参照一类非线性动力系统自由振动方程的解。

考虑方程

(24)

通过求此方程同宿轨道可得解为

(25)

取c0=0，得到满足位移不等于零，速度不等于零的初始条件，则

(26)

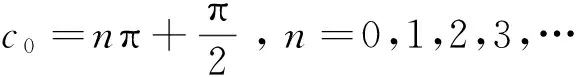
满足初速度为零的初始条件，得

(27)

5　系统稳定性分析

5.1用Floquet指数方法研究系统分岔问题

(28)

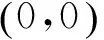
图6　相图(c′=1,β′=1)Fig.6　The phase plane (c′=1,β′=1)

当c′=2时，λ1,2=-1为相等的负数，平衡点为临界结点。在c′=2,β′=1时系统的相图如图7所示。

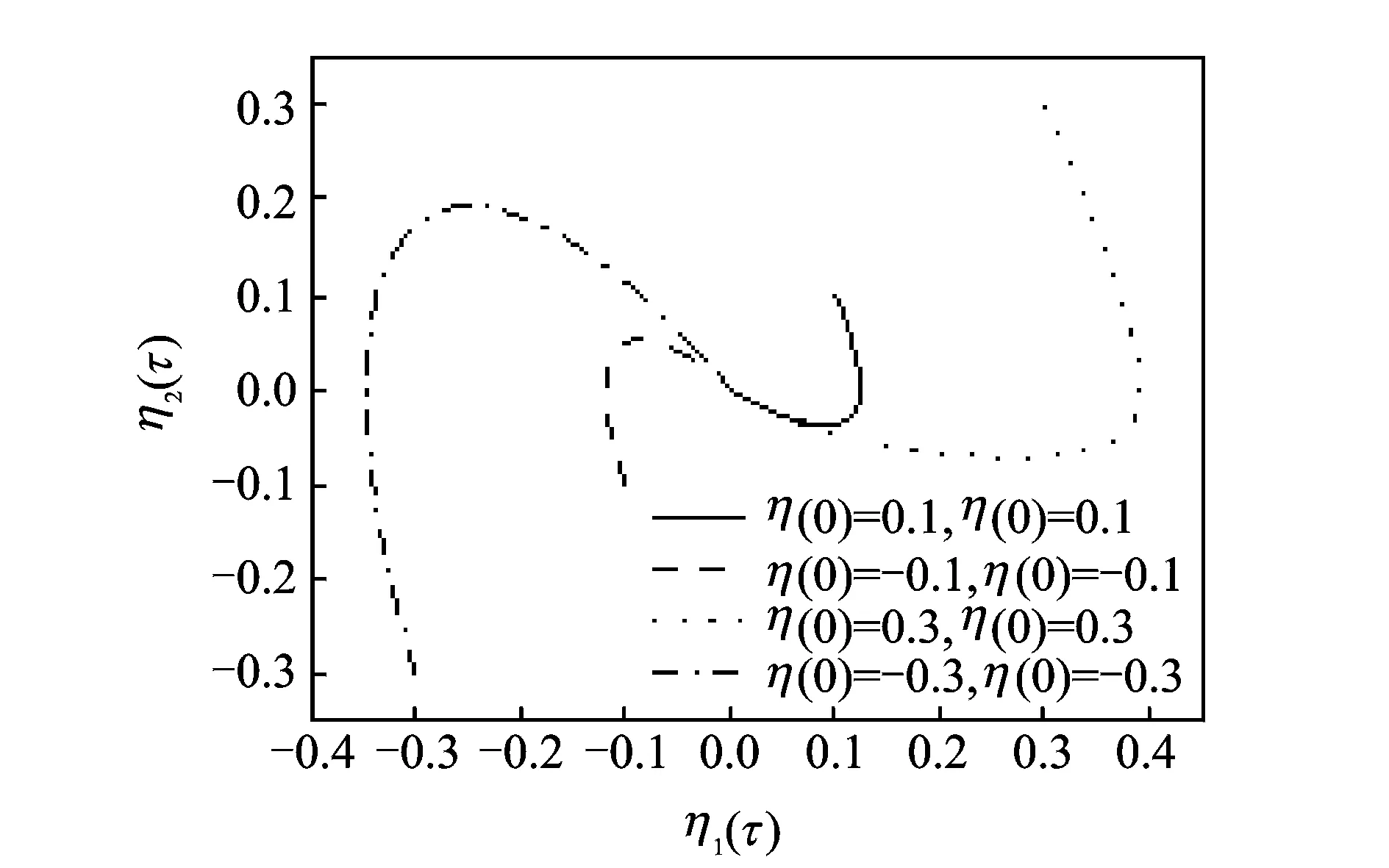
图7　相图(c′=2,β′=1)Fig.7　The phase plane(c′=2,β′=1))

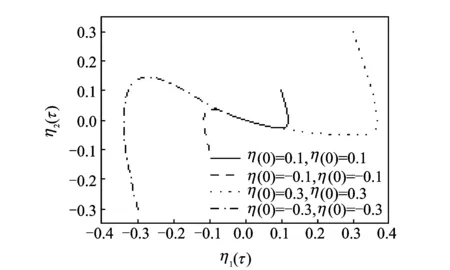
图8　相图(c′=3,β′=1))Fig.8　The phase plane(c′=3,β′=1))

当c′=0时，λ1,2=±i为纯虚数，解的曲线是极限环，发生Hopf分岔。在c′=0,β′=1时系统的相图如图9所示，为一极限环。

图9　相图(c′=0,β′=1))Fig.9　The phase plane(c′=0,β′=1))

5.2Melnikov函数

由定义的Melnikov函数[18]

(29)

经过留数计算可得

当ω=1时，

则得

(30)

当ω=3时，

则得

(31)

由式(30)，(31)可知存在同宿点，系统可能发生混沌运动。

5.3分析热耗散下热弹变形的系统分岔时螺旋角范围

根据文中给定的工况条件和分析系统稳定性的方法，计算热耗散下热弹变形的系统分岔问题时螺旋角范围

当c′=2时，α=65°43′47″时，λ1,2=-1为相等的负数，平衡点为临界结点。

当c′=0时，α=75°54′36″时，λ1,2=±i为纯虚数，解的曲线是极限环，发生Hopf分岔。

以上针对干气密封系统的稳定性进行了分析，获得了螺旋角α=75°54′36″时系统稳定运行。当螺旋角在65°43′47″<α<75°54′36″范围内，干气密封系统是稳定运行的，当螺旋角为α=65°43′47″和α=75°54′36″时，是干气密封系统稳定运行的临界点。当螺旋角在α<65°43′47″或α>75°54′36″情况下，干气密封系统将会发生混沌现象，系统运行将会不稳定。通过文献[19]利用直接数值模拟法求解轴向振动方程，计算出了当螺旋角为α=76°28′19″时，系统有混沌现象发生；当螺旋角为α=74°53′26″时，系统稳定运行，从而说明了本结论的正确性。

5.4不同条件下系统分岔时螺旋角范围

5.4.1无变形下分岔问题的螺旋角范围

无变形即是气膜在理想状态下进行工作，因此在计算时，根据干气密封系统和气膜厚度在理想状态下工作，不考虑热耗散和热弹变形对其的影响。

当c′=2时，α=66°44′50″时，λ1,2=-1为相等的负数，平衡点为临界结点。

当c′=0，α=75°45′43″时，λ1,2=±i为纯虚数。解的曲线是极限环，发生Hopf分岔。

当螺旋角α=75°45′43″时，干气密封系统是稳定的;当螺旋角在66°44′50″<α<75°45′43″范围内，干气密封系统是稳定运行的；当螺旋角为α=66°44′50″和α=75°45′43″时，是干气密封系统稳定运行的临界点；当螺旋角α<66°44′50″或α>75°45′43″情况下，干气密封系统将会发生混沌现象，系统运行将会不稳定。

5.4.2无热耗散有热弹变形的分岔问题的螺旋角范围

当c′=2，α=66°2′51″时，λ1,2=-1为相等的负数，平衡点为临界结点。

当c′=0，α=75°51′48″时，λ1,2=±i为纯虚数。解的曲线是极限环，发生Hopf分岔。

当螺旋角α=75°51′48″时，干气密封系统是稳定的。当螺旋角66°2′51″<α<75°51′48″范围内，干气密封系统是稳定运行的，当螺旋角为α=66°2′51″和α=75°51′48″时，是干气密封系统稳定运行的临界点。当螺旋角α<66°2′51″或α>75°51′48″情况下，干气密封系统将会发生混沌现象，系统运行将会不稳定。

对干气密封气膜-密封环系统轴向稳定性的分析，热耗散下热弹变形的分岔问题的螺旋角范围与无热耗散有变形和无变形的分岔问题的螺旋角范围有明显的变化。同时热耗散有变形的分叉点位置相比无热耗散有变形和无变形的分岔点更加明显。这种螺旋角失稳域的变化，说明考虑耗散下气膜-密封环流固耦合系统动态稳定性是有必要的。

6　结　论

(1)求解了临界气膜刚度和螺旋角之间的定量关系，进而求出了失稳时的螺旋角范围，并分析了失稳时系统非线性动力学行为。结果表明，在干气密封系统运行中，考虑热耗散变形对干气密封系统的稳定性有一定的影响。从螺旋角的变化来看，热耗散变形相比较无热耗散有变形和无变形的条件下更加明显。

(2)根据研究结果，可以认为考虑热耗散有热弹变形影响下，当螺旋角α=75°54′36″时，系统处于稳定运行。不同于无变形下的螺旋角数值。当干气密封系统失稳，将使得静环与动环碰撞，产生碰磨现象，令密封失效，因此考虑热耗散变形下气膜-密封环流固耦合系统动态稳定性的研究是很有工程实际的应用价值。

[1]Aimone R J，Forsthoffer W E，Salzmann R M． Dry gas seal systems: Best practices for design and selection，which can help prevent failures[J]．Turbomachinery International，2007，48(1):20—21.

[2]Krivshich N G，Pavlyuk S A，Kolesnik S A，et al． Dry gas seal systems for equipment with slow shaft rotation [J]．Chemical and Petroleum Engineering，2007，43 (11—12):676—680．

[3]Zirkelback N. Parametric study of spiral groove gas face seals[J] . Tribology Transactions, 2000,43(2):337—343.

[4]Miller B, Green I. Semi-analytical dynamic ana-lysis of spiral grooved mechanical gas face seals[J]. Journal of Tribology, 2003,125(2):403—413.

[5]Zhang Haojiong, Miller B A, Landers R G. Nonlinear modeling of mechanical gas face seal systems using proper orthogonal decomposition[J]. Journal of Tribology, 2006, 128(10):817—827.

[6]刘雨川. 端面气膜密封特性研究[D].北京:北京航空航天大学,1999.

LIU Yuchuan. Research on characteristics about face of gas film[D]. Beijing: Beijing University of Aeronautics and Astronautics, 1999.

[7]杜兆年，丁雪兴，俞树荣，等．轴向微扰下干气密封螺旋槽润滑气膜的稳定性分析[J]．润滑与密封，2006，31(10):127—130．

Du Zhaonian, Ding Xuexing, Yu Shurong, et al. A stability analysis for lubricating gaseous film of the spiral grooved gas sea is subjected to axial perturbation[J]. Lubrication Engineering, 2006,31(10):127—130.

[8]丁雪兴，王悦，张伟政，等．螺旋槽干气密封润滑气膜角向涡动的稳定性分析[J]．北京化工大学学报(自然科学版)，2008，35(2):82—86．

Ding Xuexing, Wang Yue, Zhang Weizheng, et al. A stability analysis for lubricating gaseous film of spiral grooved gas sea is subjected to angular eddy motion[J]. Journal of Beijing University of Chemical Technology(Natural Science Edition,2008, 35(2):82—86.

[9]张伟政，俞树荣，丁雪兴，等．螺旋槽干气密封系统轴向振动响应及结构优化[J]．排灌机械工程学报，2010，28(3):228—232．

Zhang Weizheng, Yu Shurong, Ding Xuexing, et al. Dynamic response of axial vibration and structural optimization for dry gas seal system with spiral groove[J]. Journal of Drainage and Irrigation Machinery Engineering,2010,28(3):228—232.

[10]俞树荣，朱丽，丁雪兴，等. 干气密封气膜-密封环系统轴向振动动力稳定性分析[J]. 振动与冲击，2012,31(15)：101—104.

Yu Shurong, Zhu Li, Ding Xuexing, et al. Nonlinear stability analysis on axial vibration of dry gas seals system with gas film and seal rings[J]. Journal of Vibration and Shock, 2012,31(15):101—104.

[11]张靖周, 常海萍. 传热学[M]. 北京: 科学出版社, 2009:97—100.

Zhang Jingzhou, Chang Haiping. Heat Transfer [M]. Beijing: China Science Press, 2009: 97—100.

[12]顾永泉. 机械密封实用技术[M]. 北京:机械工业出版社, 2002:141—145.

Gu Yongquan. Practical Technology of Mechanical Seal[M]. Beijing: China Machine Press, 2002: 141—145.

[13]丁雪兴, 蒲军军, 韩明君，等. 基于二阶滑移边界的螺旋槽干气密封气膜刚度计算与分析[J]. 机械工程学报, 2011, 47(23):119—124.

Ding Xuexing, Pu Junjun, Han Mingjun, et al. Calculation and analysis of gas gilm stiffness in the spiral groove gas seal based on the econd order slip boundary[J]. Chinese Journal of Mechanical Engineering, 2011, 47(23): 119—124.

[14]苏虹, 丁雪兴, 张海舟，等. 力变形下螺旋槽干气密封气膜流场近似计算及分析[J]. 工程力学, 2013, 30(增刊): 279—283.

Su Hong, Ding Xuexing, Zhang Haizhou, et al. Gas membrane flow field approximate calculation and analysis of spiral groove dry gas seal on the force distortion[J]. Engineering Mechanics, 2013, 30(Sup.): 279—283.

[15]张伟政，俞树荣，丁雪兴，等.螺旋槽干气密封微尺度流动场的动压计算[J].兰州理工大学学报，2006，32(6)：72—75.

ZHANG Weizheng, YU Shurong, DING Xuexing, et al. Dynamic pressure calculation of steady-state micro-scale flow field in spiral grooved dry gas seals[J]. Journal of Lanzhou University of Technology, 2006,32(6),72—75.

[16]韩明君,李有堂,朱丽,等.干气密封系统轴向非线性动力稳定性分析[J].化工机械，2012，39(03)：308—312.

HAN Mingjun, LI Youtang, ZHU Li, et al. Axial nonlinear dynamics stability of dry gas sealing system[J]. Chemical Engineening & Machinery, 2012,39(03):308—312.

[17]朱丽. 螺旋槽干气密封系统非线性动力学行为研究[D].兰州：兰州理工大学,2011.

ZHU Li. The research on nonlinear dynamic behavior of the spiral grooved gas seals[D]. Lanzhou: Lanzhou University of Technology,2011.

[18]陈士华，陆君安.混沌动力学初步[M].武汉.武汉水利电力大学出版社.1998.

Chen Shihua, Lu Junan. Principium of Chaotic Dynamics[M]. Wuhan: Wuhan University of Water Conservancy and Electrodynamics Press,1998.

[19]丁雪兴，张伟政，俞树荣，等. 螺旋槽干气密封系统非线性动力学行为分析[J]. 中国机械工程，2010,21(9):1083—1087.

Ding Xuexing, Zhang Weizheng, Yu Shurong, et al. Nonlinear dynamics behavior analysis of a spiral grooved gas seal system[J]. China Mechanical Engineering,2010,21(9):1083—1087.

Stability analysis on axial vibration of dry gas seal system under the thermo-elastic deformation considering the thermal dissipation

DINGXue-xing,LUJun-jie,LIUYong,ZHANGYing-jie

(College of Petrochemical Engineering, Lanzhou University of Technology, Lanzhou 730050, China)

Based on the nonlinear vibration theory, the axial vibration model which is about the film and seal rings in the system of dry gas seals is established. In this model, the influence of the gas film thickness and gas film stiffness are considered by the thermal dissipation and thermal-elastic deformation. A forced vibration differential equation containing nonlinear terms is derived in consideration of the nonlinear axial rigidity and damping of the gas film for the specific working conditions. The bifurcation behavior in the dry gas seal system is discussed by the Floquet exponent in the case of without external excitation.Then the influence of the spiral angle on the stability of the dry gas seal system is is analyzed. According to the above data, the range of the spiral angle that guarantee the dry gas seal system stable is given. When the spiral angle is 75°54′36″, Hopf Bifurcation occurrs. The result is compared with those of thermal-elastic deformation without thermal dissipation and of non-thermal-elastic deformation, when the Hopf Bifurcation occurres as well. The results show that the range of the spiral angle which makes the dry gas seal system stable, under thermal-elastic deformation with thermal dissipation is different from that under the thermal-elastic deformation without thermal dissipation and under non-thermal-elastic deformation. What's more, the range of the spiral angle which makes the dry gas seal system stableunder thermal-elastic deformation without thermal dissipation is closer to that under the thermal-elastic deformation with thermal dissipation. And the position of the Hopf bifurcation under thermal-elastic deformation with thermal dissipation is clearer than that under thermal-elastic deformation without thermal dissipation and non- thermal-elastic deformation. The result agree well with the result which is obtained by using the Runge-Kutta method, through which the validity of the method confirmed. Accordingly, in the future, the thermal-elastic deformation with thermal dissipation will become one of aspects which affect the stability of the dry gas seal system and will have application to the engineering practice.

nonlinear vibration; dry gas seal; thermal dissipation; bifurcation; stability

2014-06-23；

2014-11-18

国家自然科学基金资助项目(51165020)

O322; TQ051

A

1004-4523(2016)01-0078-09

10.16385/j.cnki.issn.1004-4523.2016.01.011

丁雪兴(1964—)，男，教授。电话： 15002608287； E-mail： xuexingding@163.com

陆俊杰(1990—)，男，硕士研究生。电话：15117004676；E-mail:loveljj4566@163.com