蜂窝纸板一维动态本构关系及应用*

卢富德， 高　德

(浙江大学宁波理工学院， 浙江 宁波 315100)



蜂窝纸板一维动态本构关系及应用*

卢富德， 高德

(浙江大学宁波理工学院， 浙江 宁波 315100)

为了在蜂窝纸板一维压缩应力-应变曲线基础上建立其一维本构关系，首先得到蜂窝纸板在应变率0.0017/s～114.3/s范围内的试验压缩行为。试验结果表明蜂窝纸板呈现较强的率相关性,这是由于蜂窝结构的横向惯性作用引起的。基于最低应变率0.0017/s压缩载荷下的应力-应变数据，提出了形状函数，用于精确拟合蜂窝纸板应力-应变曲线所表现的线弹性、应力软化、屈服平台和压实等四个典型特征。然后在形状函数的基础上，考虑应变率的影响，得到蜂窝纸板一维动态本构关系。最后研究了易损件-产品主体-蜂窝纸板缓冲系统在跌落冲击载荷下的冲击响应，得到缓冲系统的最大加速度-静应力曲线，所得出的结论可以直接用于具有易损件物品的缓冲设计。

蜂窝纸板; 本构关系; 应变率; 易损件; 最大加速度-静应力曲线

引　言

近年来，由于缓冲材料在运输包装的需要，利用试验的方法测试缓冲材料的应力-应变曲线，然后在这个基础上建立缓冲材料的本构模型，已被证明为一种有效设计方法[1]。传统的泡沫材料，由于不可降解性，对自然环境造成巨大的危害；多孔材料蜂窝纸板具有质轻、良好的吸收能量的能力以及对环境友好的优点，日益受到学者的关注。在对蜂窝纸板的缓冲性能研究中，文献[2]通过实验方法研究了环境相对湿度对蜂窝纸板缓冲吸收能量影响，结果表明湿度对蜂窝纸板应力-应变行为影响显著，但研究仅限于准静态压缩载荷情况；在动态冲击载荷下(最大压缩应变率约为200/s)，文献[3]试验研究了相对湿度与厚跨比耦合因素对蜂窝纸板应力-应变行为的影响；Wang[4]参考一系列应变率压缩载荷下的蜂窝纸板应力-应变曲线试验结果，综合考虑了应变率对蜂窝纸板缓冲性能的影响规律，得到了蜂窝纸板的能量吸收图。从以上的研究结果看出，学者已研究相对湿度、应变率与厚跨比等因素对蜂窝纸板缓冲性能的影响规律。

基于缓冲材料的应力-应变曲线，用一个连续的函数建立应力-应变关系，即本构模型，方便了结构的优化设计与动力学响应预测[5-7]。关于蜂窝纸板本构模型研究，文献[8]运用分段线性函数，建立蜂窝线弹性、软化、应力平台和压缩等四个区域的力学模型，近似建立蜂窝纸板吸收能量关系式。文献[9]考虑应变率因素对蜂窝纸板应力-应变曲线的线弹性、屈曲软化、屈服平台和压缩区域，分段建立对应的数学模型表征蜂窝纸板的力学行为，并利用试验数据拟合得到模型中的参数。利用分段函数拟合缓冲材料应力-应变曲线，识别参数的结果十分依赖初值的选择，甚至是不收敛，这是由于所建立的函数为分段函数，在分界点处不连续造成的，若使用连续函数就可以避免这个情况[1]。

从目前所报道的蜂窝纸板试验与本构模型研究来看，蜂窝纸板缓冲性能试验方面取得了丰富的成果，但在试验基础上所建立的蜂窝纸板本构模型，因为是用分段函数进行表达的，拟合参数时会有不易收敛的缺点，因此所建立的本构模型存在明显的不足。鉴于此，为了改进目前的蜂窝纸板本构模型，本文结合实验方法，利用一个连续函数表达式建立了蜂窝纸板的本构模型，在此基础上，研究易损件-产品主体-蜂窝纸板缓冲系统的冲击谱响应，以介绍蜂窝纸板本构方程的应用，为蜂窝纸板缓冲包装优化设计提供高效的方法。

1　蜂窝纸板试验压缩行为

1.1蜂窝纸板试验压缩应力-应变曲线

利用万能试验机和落锤试验台分别测试蜂窝纸板在异面方向的一维准静态和动态压缩行为，然后基于试验结果，得到蜂窝纸板一维本构方程。试验环境条件：相对湿度50%±3%，温度为23±3℃。所选蜂窝的夹芯克重为105 g/m2，原纸张厚度为 0.19 mm，胞元边长为 7.1 mm。对于蜂窝夹芯板的厚度，选择10，20与30 mm。测试得到压缩力与压缩位移信号，取3次试验结果的平均值，然后转化为工程应力与工程应变，为建立蜂窝纸板的本构模型提供试验基础。

图1中虚线为20 mm厚度的蜂窝纸板在压缩速率2 mm/min(压缩应变率为0.0017/s)载荷下，利用万能试验机得到的蜂窝纸板应力-应变曲线，实线为下面本构方程所计算得到的理论预测值。

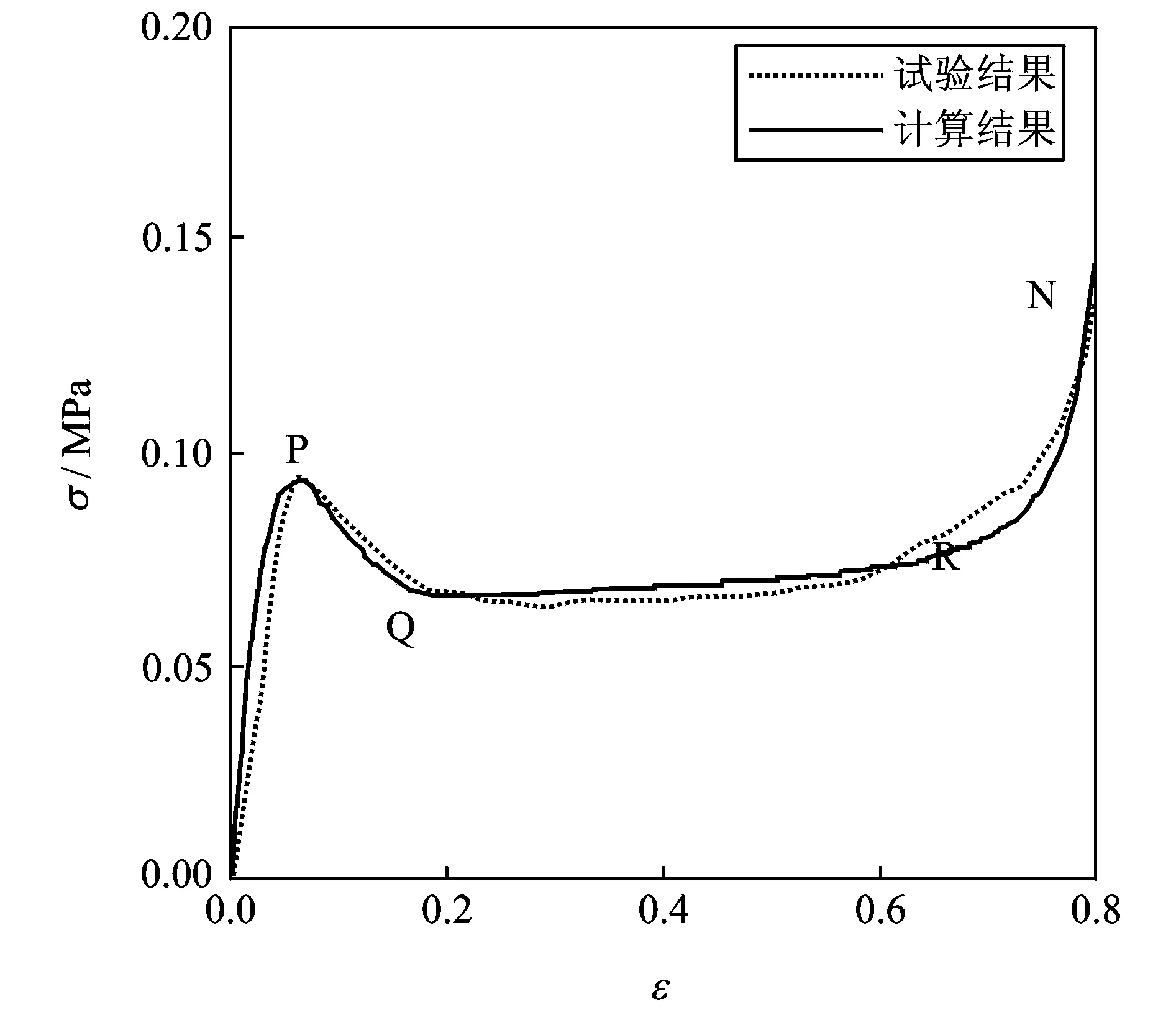
图1　蜂窝纸板准静态应力-应变曲线Fig.1　Static stress-strain curves of honeycomb paperboard

从图1可以看出，应力-应变曲线包括线弹性(OP)、应力软化(PQ)、屈服平台(QR)和压实区域(RN)4个典型区域，屈服平台区域QR为蜂窝纸板的主要吸收能量区域。因为传统泡沫的应力-应变曲线一般有线弹性、屈服平台和压实区域[1]，因此蜂窝纸板的应力-应变行为比传统泡沫多了应力软化区域，因此蜂窝纸板比泡沫力学行为更加复杂。

为研究应变率对蜂窝纸板应力-应变行为的影响，用40与250 mm/min压缩速度分别作用在厚度为20和10 mm的蜂窝纸板上，得到对应的应变率分别为0.0333和0.41/s的应力-应变曲线，如图2所示。应变率为0.0333/s载荷下蜂窝纸板平台应力为0.0905 MPa，比应变率0.0017/s时的屈服平台值0.065 MPa高出37.5%；当应变率增加到0.41/s时，蜂窝纸板屈服平台应力增加到0.113 MPa。由于不慎跌落造成的缓冲材料的应变率远远大于准静态载荷所对应的应变率，为了得到这一数量级的应变率条件下蜂窝纸板压缩应力-应变曲线，利用跌落试验台对质量为6 kg的重锤在高度为600 mm下自由跌落冲击30 mm的蜂窝纸板，即初始应变率为114.3/s，其屈服平台出现波动现象，如图2所示，对应的应变率-应变关系如图3所示。虽然跌落试验得到的应变率不是恒定的，当压缩应变为0.5时，应变率为57.4/s, 比初始应变率小49.8%，其应变率仍在一个数量级，因此利用跌落试验台所得出的应力-应变曲线仍可以把初始应变率114.3/s当作质量块压缩蜂窝纸板的应变率。图3负应变率对应蜂窝纸板卸载工况，万能试验机得到的准静态试验结果没有卸载情形的数据，因此动态数据比准静态数据多了卸载工况的结果。在应变率为114.3/s时，蜂窝纸板的平均屈服平台应力为0.165 MP，是最低应变率0.0017 /s压缩载荷下蜂窝纸板屈服平台应力0.065 MPa的2.49倍。

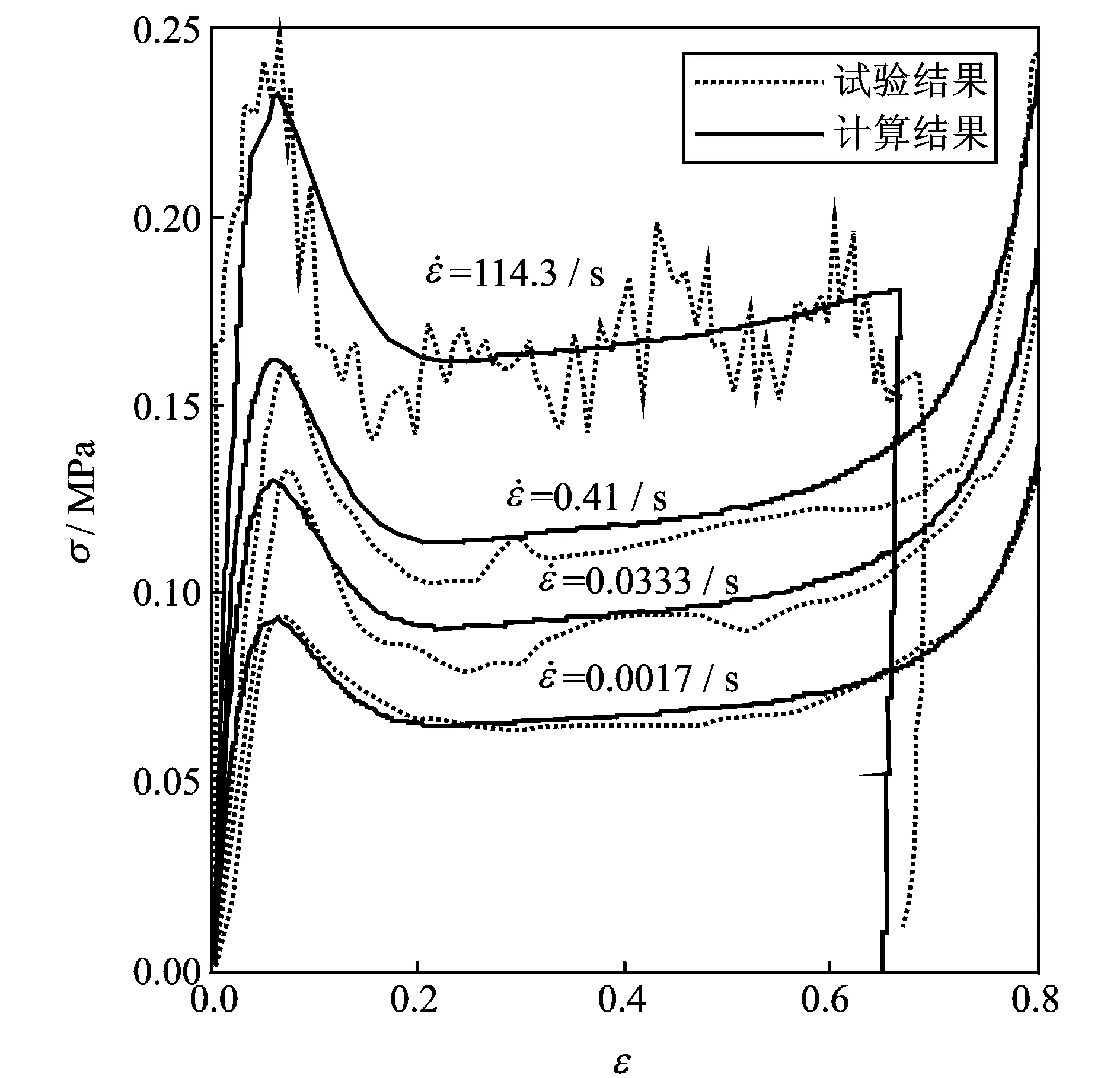
图2　应变率对蜂窝纸板应力-应变曲线影响Fig.2　Stress-strain curves of honeycomb paperboard with different compressive strain rates

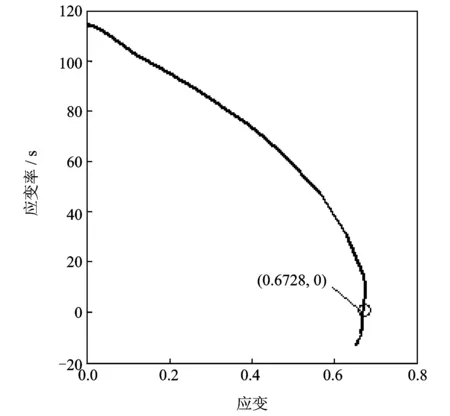
图3　应变率-应变曲线Fig.3　Strain rate-strain curve

通过上述分析，应变率对蜂窝纸板压缩行为影响显著，这与文献[4]所报道的结果一致。针对这种现象， Su[10]对缓冲结构在压缩载荷过程中发生的渐进折叠变形模式进行了分析，结果表明随压缩应变率的增加，横向惯性作用显著改变结构的变形模式，由于制作蜂窝的材料的应力-应变曲线出现应变强化，当对蜂窝结构进行快速压缩时，会出现比准静态情况下较高的应变，从而增加结构的屈服平台应力，因此蜂窝结构的率相关性是由于结构的横向惯性引起的。Hou[11]通过试验和有限元方法研究了应变率对铝蜂窝夹心板压缩行为影响规律，在结果中发现，铝蜂窝的压缩行为十分依赖应变率的大小。蜂窝纸板在变形过程中，也是发生渐进折叠现象，其应力-应变曲线依赖应变率的大小。因此应变率的改变所引起的横向惯性作用对蜂窝纸板的缓冲性能影响较大。

1.2蜂窝纸板一维本构方程

在缓冲材料的本构模型中，泡沫的本构模型比较成熟，代表性的泡沫本构框架为[12]

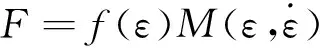
(1)

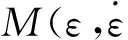
按照泡沫本构模型的做法，基于图1所示的蜂窝纸板应力-应变曲线的形状，提出蜂窝纸板压缩行为的形状函数为

(2)

式中a1～a8为待识别参数。式(2)右端的第一项表示图1所示的应力软化阶段；第二项的双曲函数表征曲线的屈服平台阶段；第三项用于拟合蜂窝纸板压实阶段的行为。这三项在应变较小时，应力-应变关系呈线性，三项线性叠加用于表征蜂窝纸板应力-应变曲线所呈现的线弹性阶段，故式(2)能满足蜂窝纸板压缩行为的线弹性、软化、屈服平台和压实等4个典型阶段。利用最小二乘法，得到表1给出的关于式(2)的参数结果，图1所示的理论结果和试验结果平均相对误差为5.21%。

在形状函数的基础上，为得到应变率对蜂窝纸板力学行为的影响，引入应变率对蜂窝纸板应力-应变曲线作用的函数[12]，如下所示

(3)

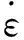
表1蜂窝纸板一维本构方程参数识别结果

Tab.1The identified results of constitutive modeling for honeycomb paperboard

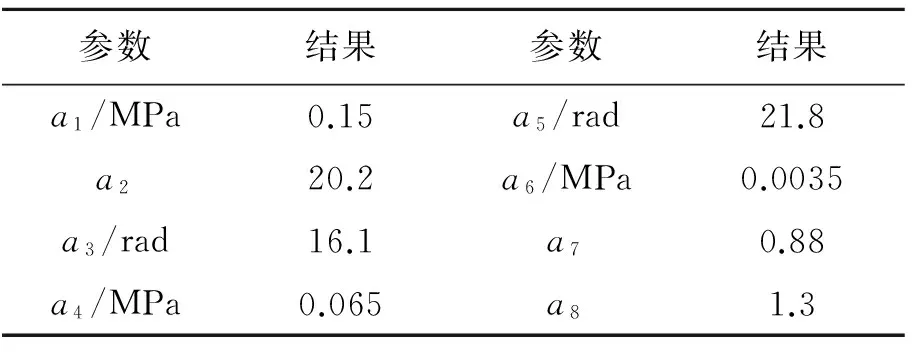
参数结果参数结果a1/MPa0.15a5/rad21.8a220.2a6/MPa0.0035a3/rad16.1a70.88a4/MPa0.065a81.3

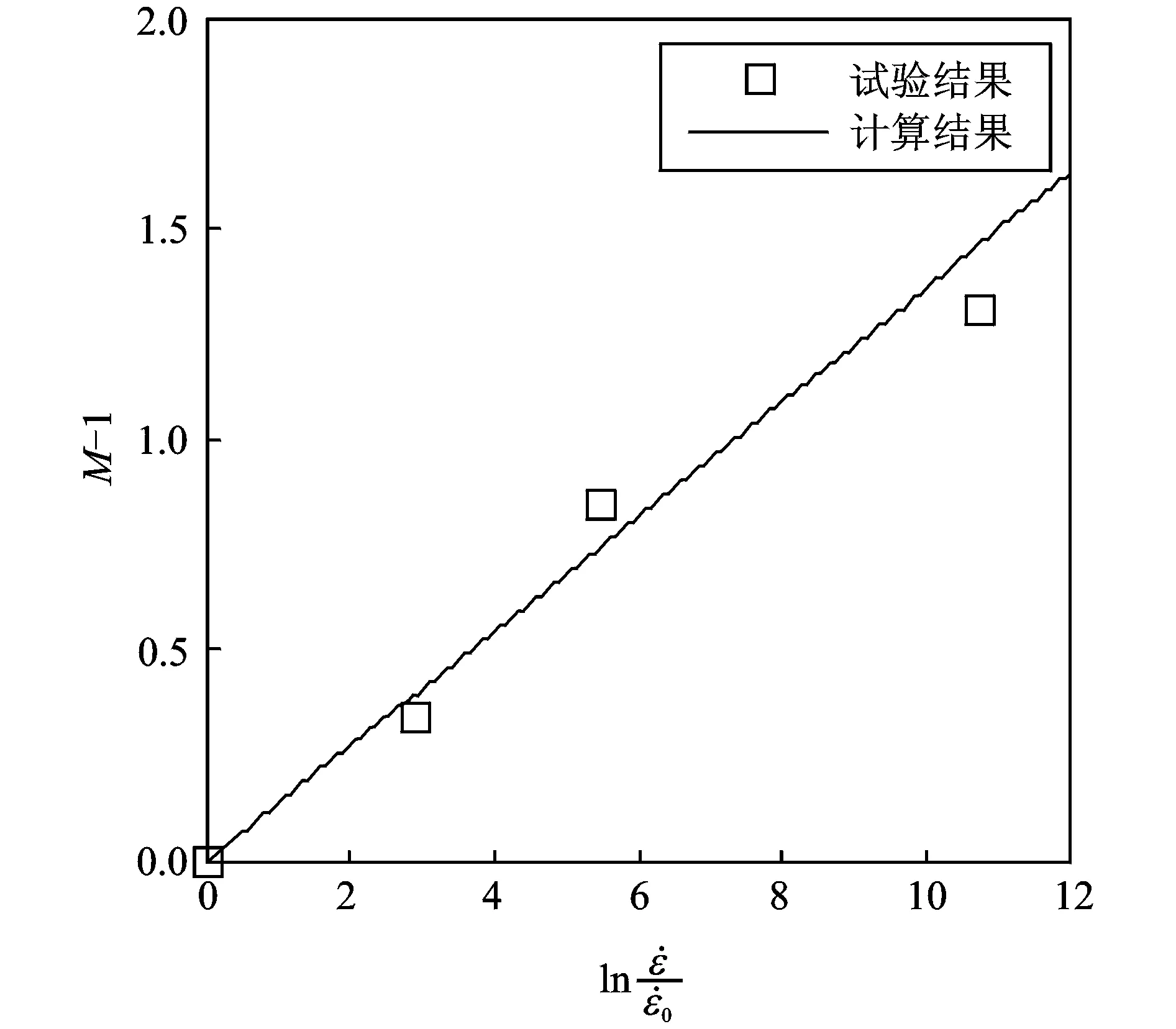
图4　M-1与的关系Fig.4　Relation between M-1 and

由于跌落压缩过程中，应变率是从最大降低到0，因为对数函数不能取0值，需要对公式(3)修正为

(4)

式(2)确定了最低应变率的应力-应变曲线所确定的形状函数，式(4)表示了应变率对蜂窝纸板应力-应变曲线影响，二者相乘，即得到蜂窝纸板一维动态本构模型

F(ε)=[a1e-a2εsin(a3ε)+a4tanh(a5ε)+

(5)

1.3试验验证

为了验证所提出的蜂窝纸板一维动态本构关系，采用蜂窝截面积为150 mm×100 mm, 厚度为20 mm, 对5 kg重锤在1000 mm高度自由跌落，得到蜂窝纸板在初始压缩应变率221.4/s下的应力-应变曲线，如图5中的虚线所示，并与计算结果进行对比。蜂窝纸板在动态冲击下的应力-应变曲线虽出现波动，但其屈服平台应力的平均值与计算结果的平均应力相对误差为4.77%，因此证明了本文所提出的蜂窝纸板一维本构模型的可靠性，可以看出本构模型较精确地拟合了蜂窝纸板的线弹性、应力软化、屈服平台和压实4个典型区域。

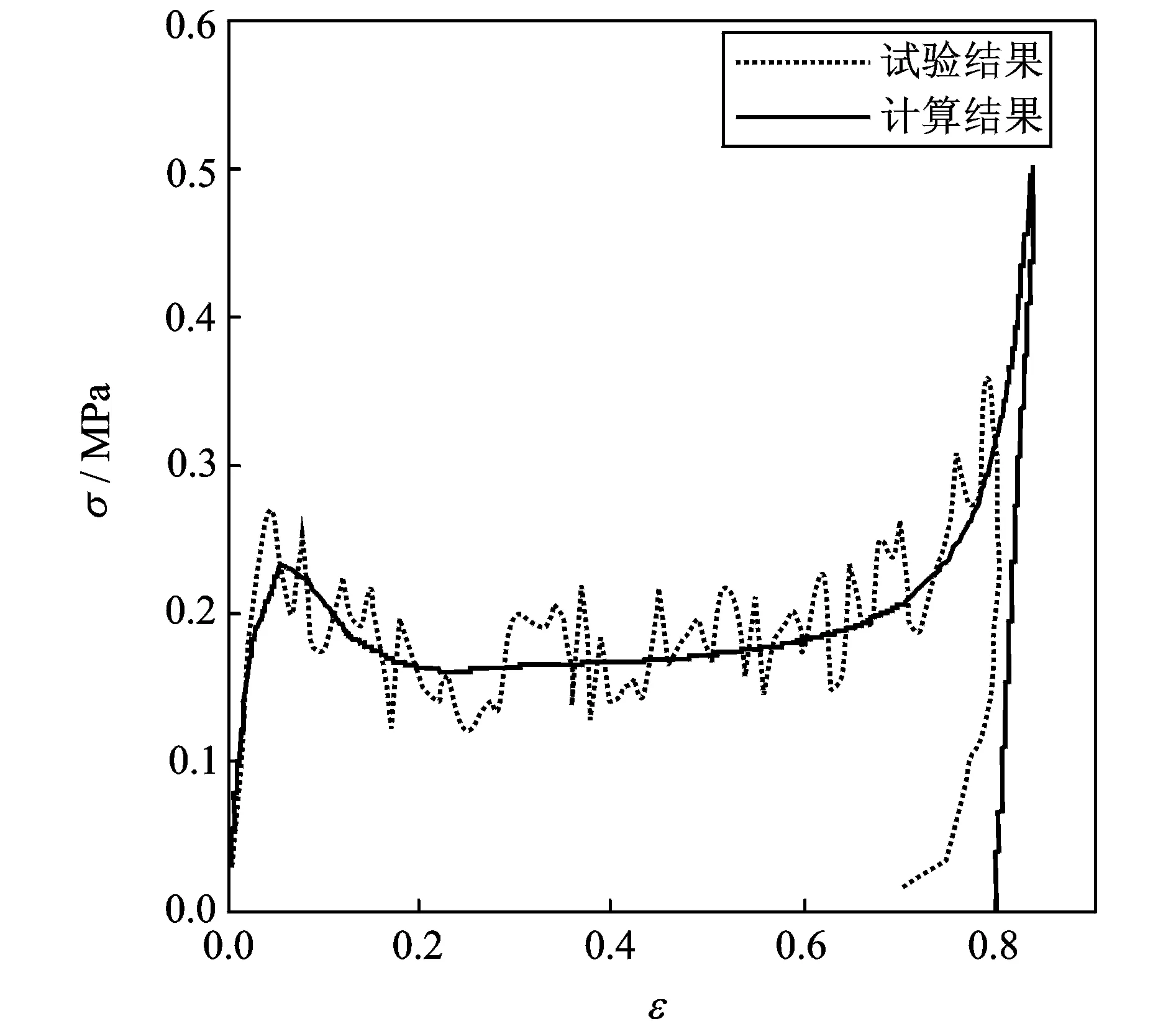
图5　蜂窝纸板应力-应变试验结果与计算结果对比Fig.5　Comparison between experimental and theoretical stress-strain curves of honeycomb paperboard

2　蜂窝纸板本构方程的应用

典型电子或光学产品的破坏是由于内部的关键部件决定的，称为易损件，例如电路板[13]，这些部件的破坏会导致产品整体功能的失效；对于蜂窝纸板缓冲作用下的电子产品，当电子产品由于跌落原因冲击压缩蜂窝纸板时，传递到产品上的加速度脉冲明显不同于冲击试验所用到的半正弦加速度脉冲，这时需要把蜂窝纸板缓冲作用下的实际加速度脉冲作为输入激励，对产品易损件的冲击响应进行评估，方能得到与实际相符合的冲击响应规律[14-15]。

2.1易损件-产品主体-蜂窝纸板缓冲系统

研究具有集中质量易损件的产品在蜂窝纸板缓冲作用下的动力学行为，所建立的集中质量易损件-产品主体-蜂窝纸板缓冲系统在高度H自由跌落示意图如图6所示。

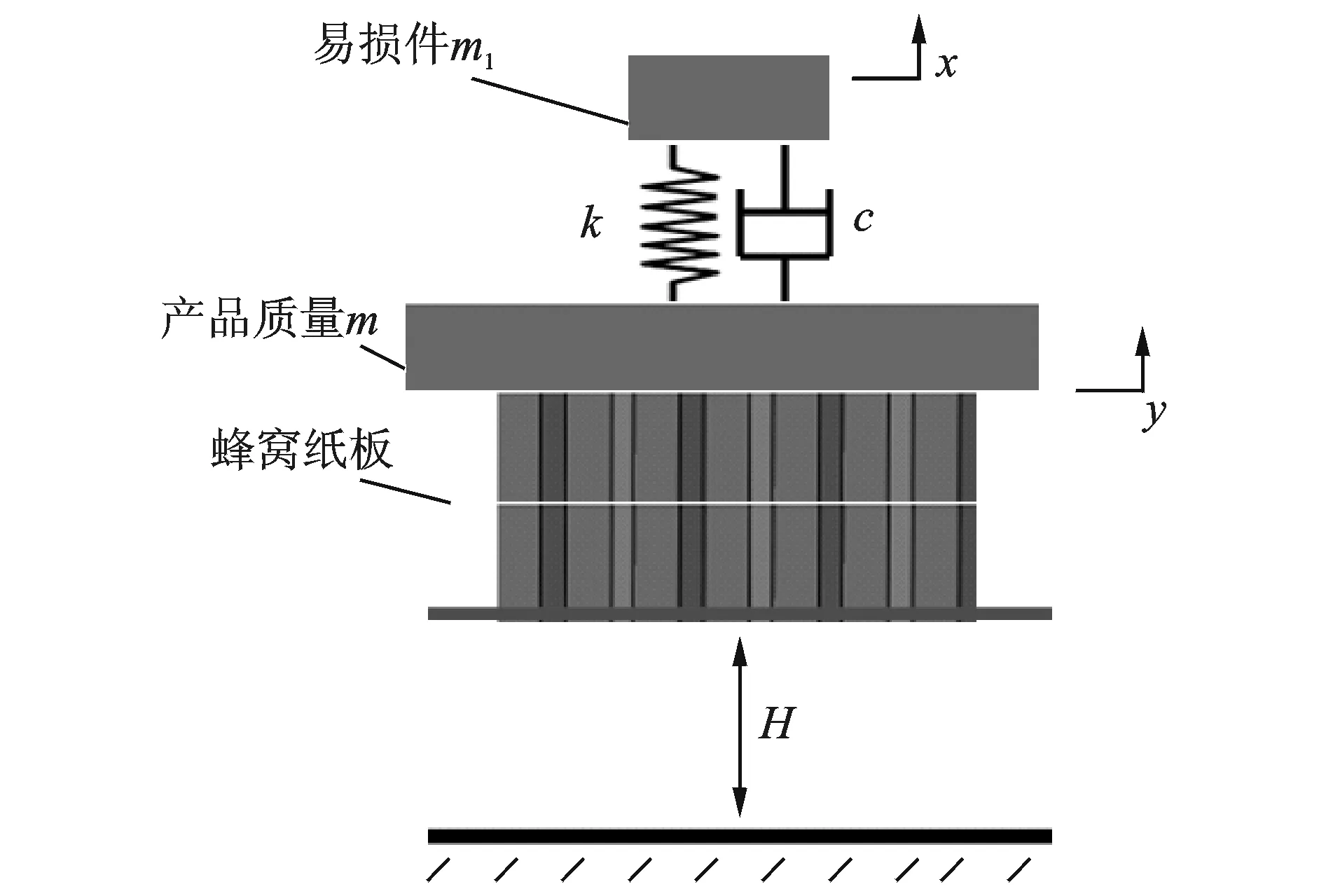
图6　易损件-产品主体-蜂窝纸板缓冲系统示意图Fig.6　Schematic diagram of critical component-main body-honeycomb paperboard cushioning system

取蜂窝纸板落地的瞬间为缓冲系统的初始时刻，x，y分别用于表示易损件与产品的运动，因此图6所示的缓冲系统动力学方程为

(6)

初始条件为：

(7)

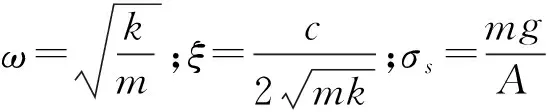
(8)

由式(7)，(8)可知，易损件冲击响应仅与参数H，h，ω，ξ和σs有关。

2.2易损件冲击响应

取参数H=700 mm,ω=503 rad,ξ=0.3,σs=3.5 kPa。作为一个例子，当厚度取15 mm时，蜂窝纸板对质量块作用的冲击脉冲如图7所示。图中也给出了易损件的加速度响应，可以看出易损件在加速度脉冲作用下出现了振动。为了分析蜂窝纸板厚度对缓冲系统响应的影响，取蜂窝纸板厚度h从12 mm到50 mm之间变化，得到质量块的加速度脉冲如图8(a)所示，和易损件在图8(a)所示的加速度激励下的响应如图8(b)所示。当蜂窝纸板厚度为12 mm时，蜂窝纸板已“触底”，随着厚度的增加，蜂窝纸板所呈现的冲击脉冲不再变化，经计算表明，13.5 mm为蜂窝纸板在上述参数作用下的临界厚度，当大于13.5 mm的厚度，易损件冲击响应不再变化。

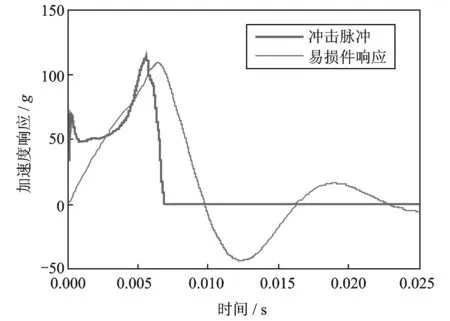
图7　易损件-产品主体-蜂窝纸板冲击响应(h=15 mm)Fig.7　Impact responses of critical component-main body-honeycomb paperboard cushioning system (h=15 mm)

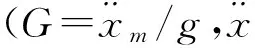
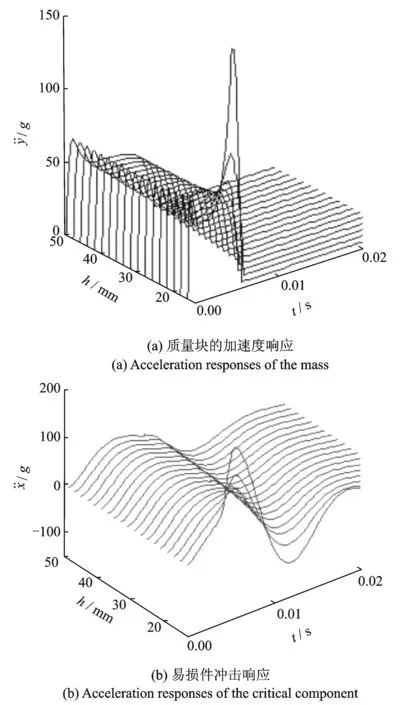
图8　蜂窝厚度对缓冲系统冲击响应的影响Fig.8　The effect of thickness of honeycomb paperboard on the impact responses of cushioning system

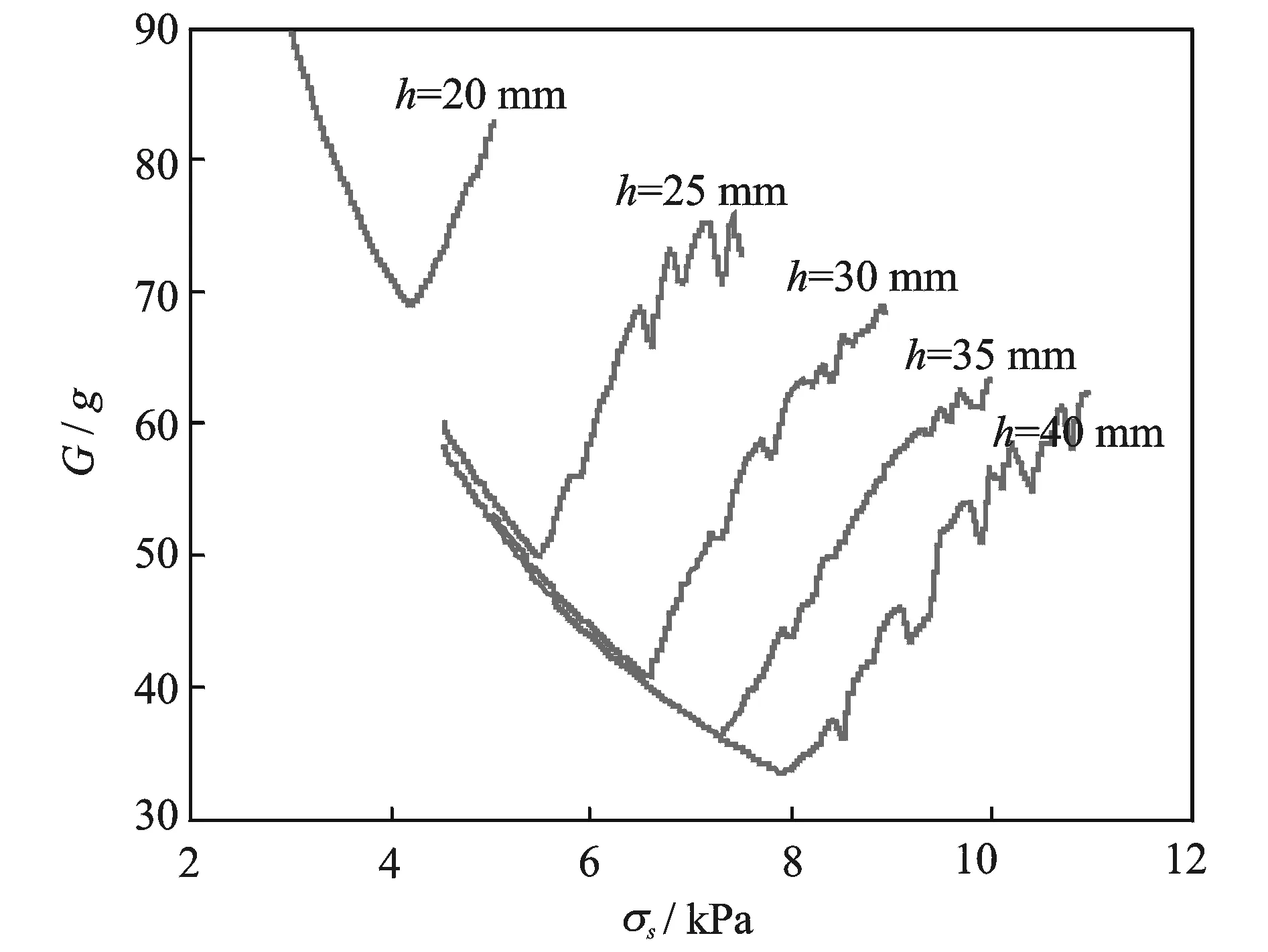
图9　最大加速度-静应力曲线Fig.9　Maximum acceleration-static stress

给定跌落高度与易损件的刚度等参数值，利用得到的蜂窝纸板的一维动态本构模型，即可得到缓冲系统最大加速度-静应力曲线，然后按照易损件的容许加速度，即可设计蜂窝纸板的横截面积与厚度，从而实现了科学设计蜂窝纸板在缓冲中的应用。

3　结　论

(1)在准静态和动态应变率范围，对蜂窝纸板在异面方向进行压缩试验研究，在最低应变率载荷下，对线弹性、应力软化、屈服平台和压实区域等4个典型特征建立了蜂窝纸板应力-应变曲线的形状函数；应变率对蜂窝纸板应力-应变曲线影响显著，因为随压缩应变率的增加，横向惯性作用显著改变蜂窝结构在压缩过程中的变形模式，从而增加结构的屈服平台应力。在形状函数的基础上，进而考虑应变率影响，得到蜂窝纸板一维本构关系。

(2)建立了易损件-产品主体-蜂窝纸板缓冲系统动力学模型，给定参数H，h，ω，ξ和σs的值,得到易损件的冲击响应，并分析了缓冲系统的最大加速度-静应力曲线，这个最大加速度为易损件响应加速度，与传统最大加速度-静应力曲线所指的质量块加速度不同。因此，本文所得出的最大加速度-静应力曲线可用于具有易损件产品的缓冲设计，而传统的最大加速度-静应力曲线因未考虑易损件为产品的破坏元件，则不能用于具有易损件产品的缓冲设计。

[1]Avalle M, Belingardi G, Ibba A. Mechanical models of cellular solids: Parameters identification from experimental tests[J]. International Journal of Impact Engineering, 2007,34(1):3—27.

[2]E Y P, Wang Z W. Effect of relative humidity on energy absorption properties of honeycomb paperboards[J]. Packaging Technology and Science, 2010,23(8):471—483.

[3]王志伟,姚著.蜂窝纸板冲击压缩的试验研究和有限元分析[J].机械工程学报，2012,48(12)：49—55.

WANG Zhiwei, YAO Zhu. Experimental investigation and finite element analysis for impact compression of honeycomb paperboards[J]. Journal of Mechanical Engineering, 2012,48(12):49—55.

[4]Wang Z W, E Y P. Energy-absorbing properties of paper honeycombs under low and intermediate strain rates[J]. Packaging Technology and Science, 2012,25(3):173—185.

[5]Zhang J, Kikuchi N, Li V, et al. Constitutive modeling of polymeric foam material subjected to dynamic crash loading[J]. International Journal of Impact Engineering, 1998,21(5):369—386.

[6]Jeong K Y, Chon S S, Munshi M B. A constitutive model for polyurethane foam with strain rate sensitivity[J]. Journal of Mechanical Science and Technology, 2012,26(7):2033—2038.

[7]Liu Q, Subhash G.A phenomenological constitutive model for foams under large deformation[J]. Polymer Engineering and Science,2004,44(5):463—473.

[8]Wang Z W, E Y P . Mathematical modelling of energy absorption property for paper honeycomb in various ambient humidities[J]. Materials & Design,2010,31(9):4321—4328.

[9]卢富德，高德.考虑蜂窝纸板箱缓冲作用的产品包装系统跌落冲击研究[J].振动工程学报，2012,25(3):335—341.

LU Fude, GAO De. Study on drop impact of packaging system considering the cushioning action of honeycomb paperboard box[J]. Journal of Vibration Engineering, 2012,25(3)：335—341.

[10]Su X Y,Yu T X,Reid S R. Inertia-sensitive impact energy-absorbing structures, Part I: effects of inertia and elasticity[J]. International Journal of Impact Engineering, 1995,16(4):651—672.

[11]Hou B, Zhao H, Pattofatto S, et al. Inertia effects on the progressive crushing of Aluminium honeycombs under impact loading[J]. International Journal of Solids and Structures, 2012,49:2754—2762.

[12]Sherwood J A, Frost C C. Constitutive modeling and simulation of energy absorbing polyurethane foam under impact loading[J].Polymer Engineering and Science,1992,32(16):1138—1146.

[13]Zhou C Y, Yu T X. Analytical models for shock isolation of typical components in portable electronics[J]. International Journal of Impact Engineering, 2009,36(12):1377—1384.

[14]Wang J, Duan F, Jiang J, et al. Dropping damage evaluation for a hyperbolic tangent cushioning system with a critical component[J]. Journal of Vibration and Control, 2012,18(10):1417—1421.

[15]Garcia-Romeu-Martinez M A, Sek M A, Cloquell-Ballester V A. Effect of initial pre-compression of corrugated paperboard cushions on shock attenuation characteristics in repetitive impacts[J]. Packaging Technology and Science,2009,22(6):323—3345.

[16]Sek M, Minett M. A new method for the determination of cushion curves[J]. PackagingTechnology and Science,2000,13(6):249—255.

One-dimension constitutive relationship and its application for honeycomb paperboard

LUFu-de,GAODe

(Ningbo Institute of Technology， Zhejiang University， Ningbo 315100, China)

A series of quasi-static and dynamic uniform compressive testes with the strain rates from 0.0017/s to 114.3/s are performed in order to establish constitutive relationship for honeycomb paperboard subjected to one-dimensional compressive loading condition. The experimental results show that the honeycomb paperboard exhibits obvious rate dependency, which is caused by lateral inertia effect of honeycomb structure. The shape function capturing relationship between stress and strain is proposed on the basis of the experimental data at the lowest strain rate of 0.0017/s, which can accurately characterize linear elastic, stress drop, yielding plateau and densification region of stress-strain curve of honeycomb paperboard. Then dynamic constitutive equation of honeycomb structure is obtained by considering the effect of strain rate on compressive behaviors based on the shape function. Finally, impact responses of cushioning system consisting of vulnerable components, main body of product and honeycomb paperboard are analyzed and the maximum acceleration-static stress curves are derived, which can provide guidance for cushioning packaging design of products comprising vulnerable components under the action of honeycomb paperboard.

honeycomb paperboard; constitutive relationship; strain rate; critical component; maximum acceleration-static stress curves

2014-08-24；

2015-05-21

国家自然科学基金资助项目 (11402232)；宁波市自然科学基金资助项目(2015A610092)

TB485.1; O322

A

1004-4523(2016)01-0038-07

10.16385/j.cnki.issn.1004-4523.2016.01.006

卢富德(1982—)，男，讲师，博士。电话： 15168139787; E-mail: lu673153@163.com