柔性梁含摩擦斜碰撞的刚体-弹簧-质点混合模型研究*

沈煜年， 顾金红

(南京理工大学力学与工程科学系， 江苏 南京 210094)



柔性梁含摩擦斜碰撞的刚体-弹簧-质点混合模型研究*

沈煜年， 顾金红

(南京理工大学力学与工程科学系， 江苏 南京 210094)

为精确快速地预测柔性梁因斜碰撞导致的复杂瞬态动力响应，提出了一种可同时计及局部接触区法向接触柔度、切向接触柔度以及柔性梁整体结构柔度的混合分析模型(HAM)。基于有限段法的思想，将柔性梁的整体位移场离散为弹簧-阻尼-刚体系统，局部接触区的法向双线性压缩-恢复以及切向摩擦变形过程则用含有能量恢复系数的弹塑性弹簧-质点系统进行描述。依据HAM模型，导出了斜碰撞系统在不同接触状态下的分段连续动力学方程。给出了法向压缩-恢复状态和切向黏-滑运动状态的切换准则，并运用事件驱动法对数值算例进行了求解。通过比较HAM模型解、实验数据以及商业有限元解，表明该模型能准确预测接触力的时间历程并描述反复切换的黏-滑(反向)运动模式，验证了HAM模型的可行性。

非线性振动； 斜碰撞； 切向柔度； 摩擦接触； 黏-滑运动

引　言

斜碰撞不仅存在于宏观大尺度宇宙天体之间[1]，而且在机械工程、航空航天甚至微尺度机械领域中也是频繁出现的现象[2]。例如空间探测器的交会对接[3]、飞行器表面的粒子侵蚀[4]、机械手抓取货物的冲击作用[5]、齿轮对的相互拍击[6]、金属的爆炸焊接工艺[7]以及微小管道机器人的管内运动[8]等。少数情形人们会利用含摩擦斜碰撞去实现机构特定的功能目的；但更多的情况则是斜碰撞会带来结构失效、增加噪音以及安全性降低等许多不利的一面[9-12]。

斜碰撞发生时，碰撞结构不仅在接触面的法向存在一个单边约束，而且在切向还有一个摩擦约束[13]。相比正碰正碰撞，斜碰撞的瞬态特征更加复杂，切向约束会导致接触面间的黏滞-微滑动(有时会反向)[14]。Johnson[15]在研究具有初始角速度的超弹性球体斜向撞击水平地面时，发现了一个运用刚体碰撞模型无法解释的特殊现象，即球质心速度的水平分量以及转动角速度在斜碰撞后均会发生反向。通过分析，其认为接触区较大的切向柔度可能是该现象产生的根本原因。Stronge[16]和Shen[14]考虑硬质碰撞物体接触区的切向柔度，非接触区部分仍视为刚体，建立能分析接触点反向滑动的集中参数模型，讨论了接触柔度对接触点的切向速度和接触力影响。然而，斜碰撞事件中接触与分离的状态切换(即接触约束的添加和删除)会使杆和梁等可变形体的振动模态发生突变，且接触区产生弹塑性变形。这些特征均与结构的柔性密切相关，目前尚缺乏深入研究。

本文将前述文献的研究进行了发展，提出了一种可同时计及局部接触区法向接触柔度、切向接触柔度以及柔性梁整体结构柔度的混合分析模型(HAM)，用以研究柔性梁的含摩擦斜碰撞问题。基于有限段法思想，将柔性梁的整体位移场离散为弹簧-阻尼-刚体系统。局部接触区的法向双线性压缩-恢复过程以及切向摩擦变形过程用含有能量恢复系数的弹塑性弹簧-质点系统进行描述。根据所建混合模型，推导了斜碰撞系统在不同接触状态下的分段连续动力学方程，给出了法向压缩-恢复状态和切向黏-滑运动状态的切换准则，并运用事件驱动法对数值算例进行了求解。验证了本文模型的可行性。

1　斜碰撞混合分析模型

如图1(a)所示，考虑一个端部为半圆头的圆形截面柔性梁以初始平动速度V斜向撞击粗糙刚性地面。梁长为L、横截面积为A、材料的杨氏模量为E、质量密度为ρ、泊松比为ν。梁的轴线与x轴正向夹角为u。首先基于有限段思想将柔性梁整体分割成若干离散段[17](如图1(b)所示)，建立梁整体的弹簧-阻尼-刚体系统，然后引入考虑切向接触柔度的弹塑性弹簧-质点系统用以描述接触效应和计算接触力。通过联合前述两个子系统，可建立斜碰撞刚体-弹簧-质点混合模型。

1.1柔性梁整体的弹簧-阻尼-刚体系统

如图1(b)所示，将柔性梁等分成n段，每段长度和质量分别为l=L/n和m=ρAl。为了同时考虑梁的轴向变形和弯曲变形，相邻的离散段之间通过两根关于中心轴对称分布的、弹簧刚度为K的弹簧阻尼器联接，弹簧距中心轴的距离为a/2。梁的轴向弹性通过选择适当的拉压刚度K值确定，梁的弯曲刚度由弹簧距离a来确定。梁端部与粗糙表面的接触效应由1.2节中的局部接触模型进行描述。该模型可以计算斜碰撞过程中的法向接触力F3和切向摩擦力F1，以及刻画黏滞-微滑动运动模式。

图1(b)所示离散系统具有2n+1个自由度，用来描述其运动状态的广义坐标列向量可表示为

X=(x0,y0,u0,q1,u1,u2,…,qn-1,un-1)T

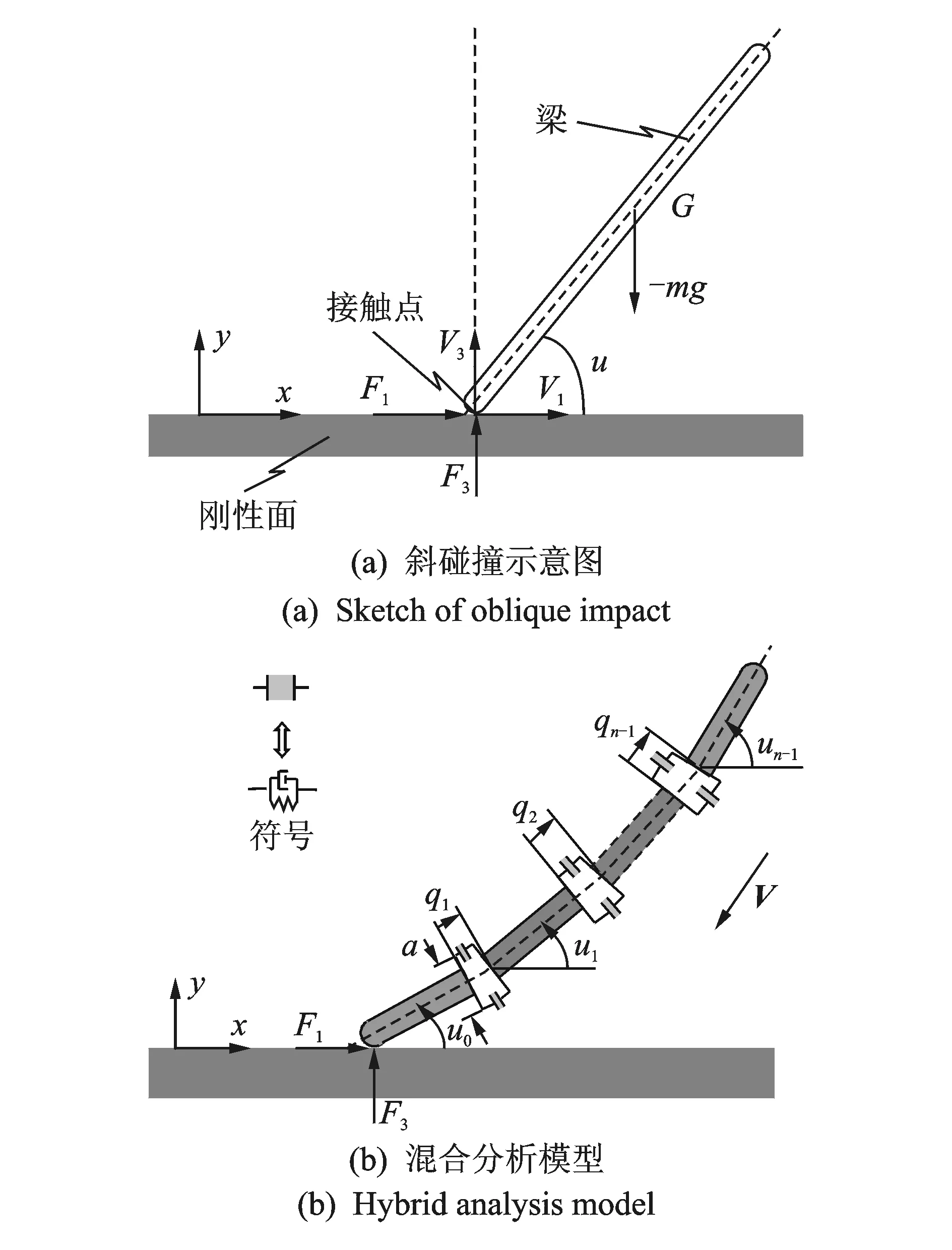
图1　柔性梁斜向碰撞粗糙刚性地面Fig.1　Flexible beam oblique impact against rough rigid ground

式中x0和y0分别为接触点在笛卡尔坐标系x-o-y中的位置坐标，ui(i=0,1，…，n-1)为第i+1个离散段与x轴的夹角。qi为第i+1个离散段离散截面圆心到第i个离散段离散截面的垂直距离。第i个离散段的质心点的位置(xic,yic)可表示为

(1)

离散系统的总动能T为

(2)

式中Jc为每小段对其质心的转动惯量。由于梁碰撞引起的振动衰减发生在几秒内，而碰撞发生在几百个微秒之内，因此本文忽略梁内部阻尼对碰撞瞬态响应的影响[17]。系统总势能V(取y=0处为势能零点)为

(3)

作用于系统的广义力向量Q由非保守力Q′(即接触端的接触力)和保守力向量Q″(即重力)叠加而成，系统的运动可由含有接触力的第二类拉格朗日方程表示为

(4)

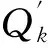
将公式(2)和(3)代入方程(4)，由符号运算软件得到2n-1个方程组成的非线性动力学方程组

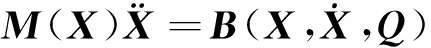
(5)

式中M为系统总体质量阵，B为关于广义位移、广义速度和外力的列向量。下面运用胡克定律和欧拉伯努利方程估算离散段之间弹簧单元的刚度K和a。

(1)离散模型的轴向变形

假设梁在自身重力的单独作用下，该梁垂直悬挂于空间中。此时均质连续梁的质心处产生的轴向静位移δc为

(6)

同时，对于离散梁模型，该点的位移δd又可用梁上半部分的段间弹簧变形量计算得到

(7)

由δc=δd，可解得拉压刚度K

(8)

(2)离散模型的弯曲变形

根据连续悬臂梁的弯曲理论，可获得在重力单独作用下悬臂梁质心位置的转角为

(9)

式中Iz为横截面对z轴的惯性矩(对圆截面的梁有Iz=πd4/64)。由于是小变形问题，离散梁模型中第i段的力矩平衡方程为

(10)

式中φi为第i-1段与第i段之间的相对转角。方程(10)中的第1项是由重力引起的，第2项是第i+1段和第i段之间弹簧的作用力矩。此外，第i+1段的绝对转角ui可写成如下形式

(11)

将式(10)和(11)联立，可获得中心段的转角为

(12)

由uc=ud，得到

(13)

式中a只与段数n和梁横截面参数有关。

1.2局部接触区的弹塑性弹簧-质点系统

本文分别采用双线性柔性单元和线性柔性单元描述接触区的法向弹塑性变形效应和切向变形效应[14]，建立了如图2所示局部接触区的弹塑性弹簧-质点系统。

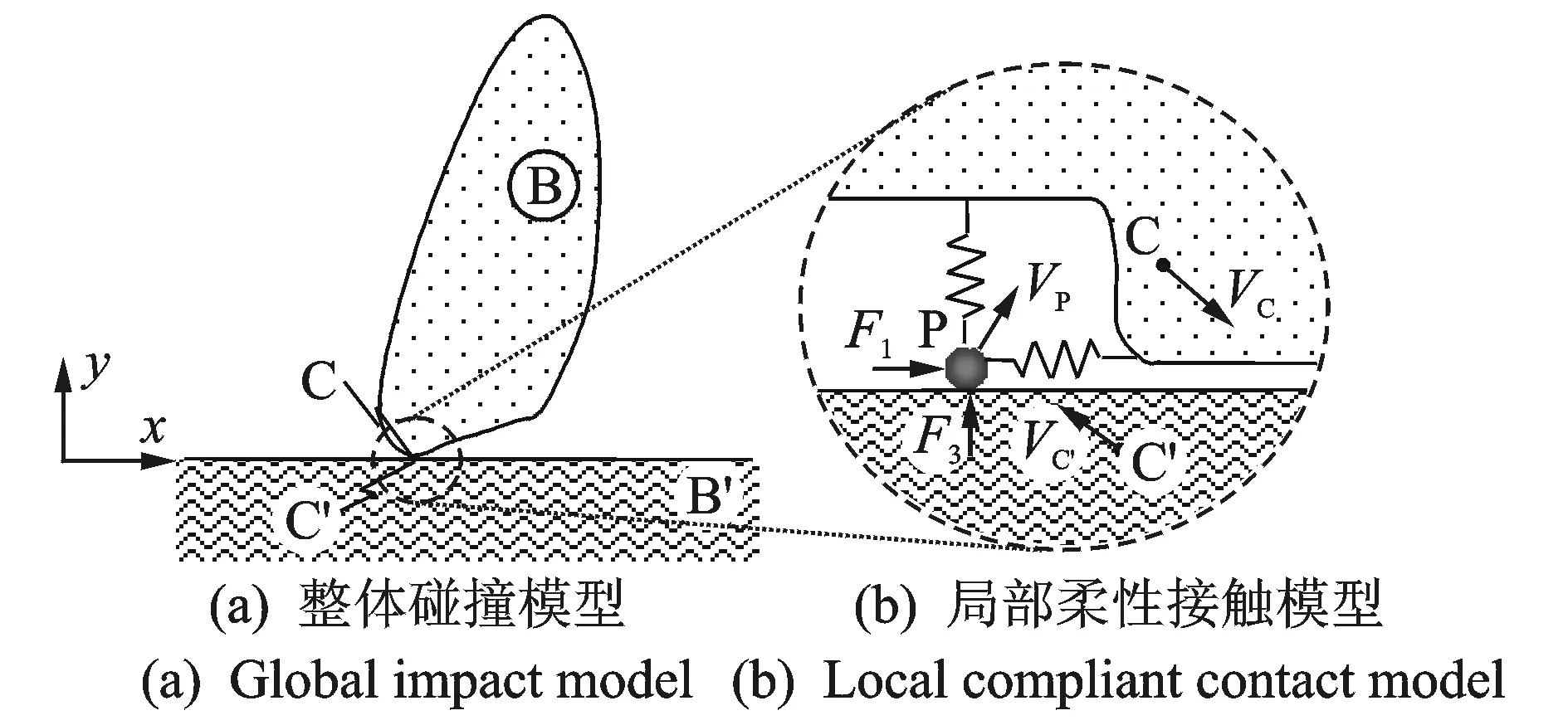
图2　平面含摩擦斜碰撞局部弹性接触模型Fig.2　Hybrid analytical model for planar impact with friction

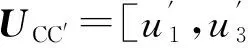
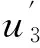
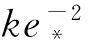
(14)

(15)

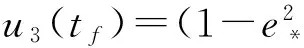
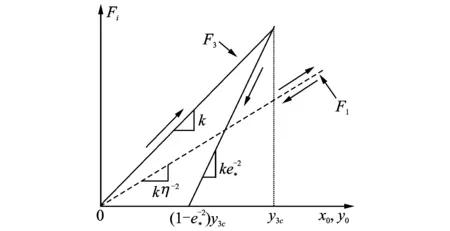
图3　法向和切向柔性单元的力与变形量的关系Fig.3　Force-deflection relation for normal and tangential compliant elements

此运动过程中法向接触力和切向接触力满足Coulomb摩擦定律

(16)

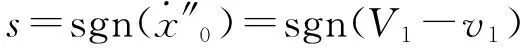
2　接触状态的判断标准

斜碰撞问题除了会导致法向存在一个压缩和恢复阶段的切换，在切向还存在滑动和黏滞状态的切换。在使用事件驱动法求解碰撞响应时，需要判断接触所处的状态。假设切向由黏滞切换为滑动的时刻为t01，从滑动切换为黏滞的时刻为t10。各状态的判断标准如下：

(1)初始状态

在碰撞初始时刻(t=0)，法向接触处于压缩阶段。切向初始黏滞的条件为

(17)

反之，一旦入射角大于μη2，则切向的初始状态为滑动。

(2)压缩或恢复阶段

在碰撞的初始阶段，接触为压缩阶段。压缩阶段结束和恢复阶段开始于tc时刻，此时法向相对速度消失，即满足

(18)

(3)黏滞或滑动

(19)

相反地，如果系统之前处于滑动状态，当质点P和接触点C′间的相对速度消失，变为零时，此时记为t10时刻，系统开始由滑动状态转变为黏滞状态，即

(20)

(4) 碰撞结束

若在tf-ε时刻法向接触力为正(即F3(tf-ε)>0)，在tf+ε时刻法向接触力为正(即F3(tf+ε)<0)，其中ε是一个正数小量，则认为碰撞结束的时刻为tf，法向接触力将会消失为零，即

(21)

3　算　例

若无特殊说明，算例的系统参数为：柔性梁的长度为1 m，圆形横截面面积为10-4m2，梁的接触端部为半圆头，材料为钢(即杨氏模量为210 GPa，质量密度为7 800 kg/m3，泊松比为0.3)。梁的法向初始平动速度y0=-1 m/s，切向初始平动速度为x0=3.5 m/s。梁初始时刻与刚性平面接触，无相对转动。梁的轴线与x轴正向夹角为3π/4，即u0=3π/4。

Johnson[16]认为在法向作用力P的准静态作用下接触圆面的半径a可表示为(3PR/(4E*))1/3，其中E*和R可以由下式计算得到：

(22a)

(22b)

式中νi，Ei和Ri分别为接触物体i(i=1, 2)泊松比、弹性模量以及接触端的半径。接触区法向刚度k的计算表达式为

(23)

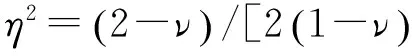
3.1收敛性研究

首先研究了HAM模型的数值结果收敛性，获得结构的合理离散密度。假设恢复系数e*=1，摩擦系数为μ=2/3，获得的法向最大压下量值的收敛曲线如图4所示。结果表明，当n=44，接触点最大法向压下量已经趋于稳定值，故本文后面计算中在柔性梁长度不变的情况下，离散段数均取n=50进行数值计算。

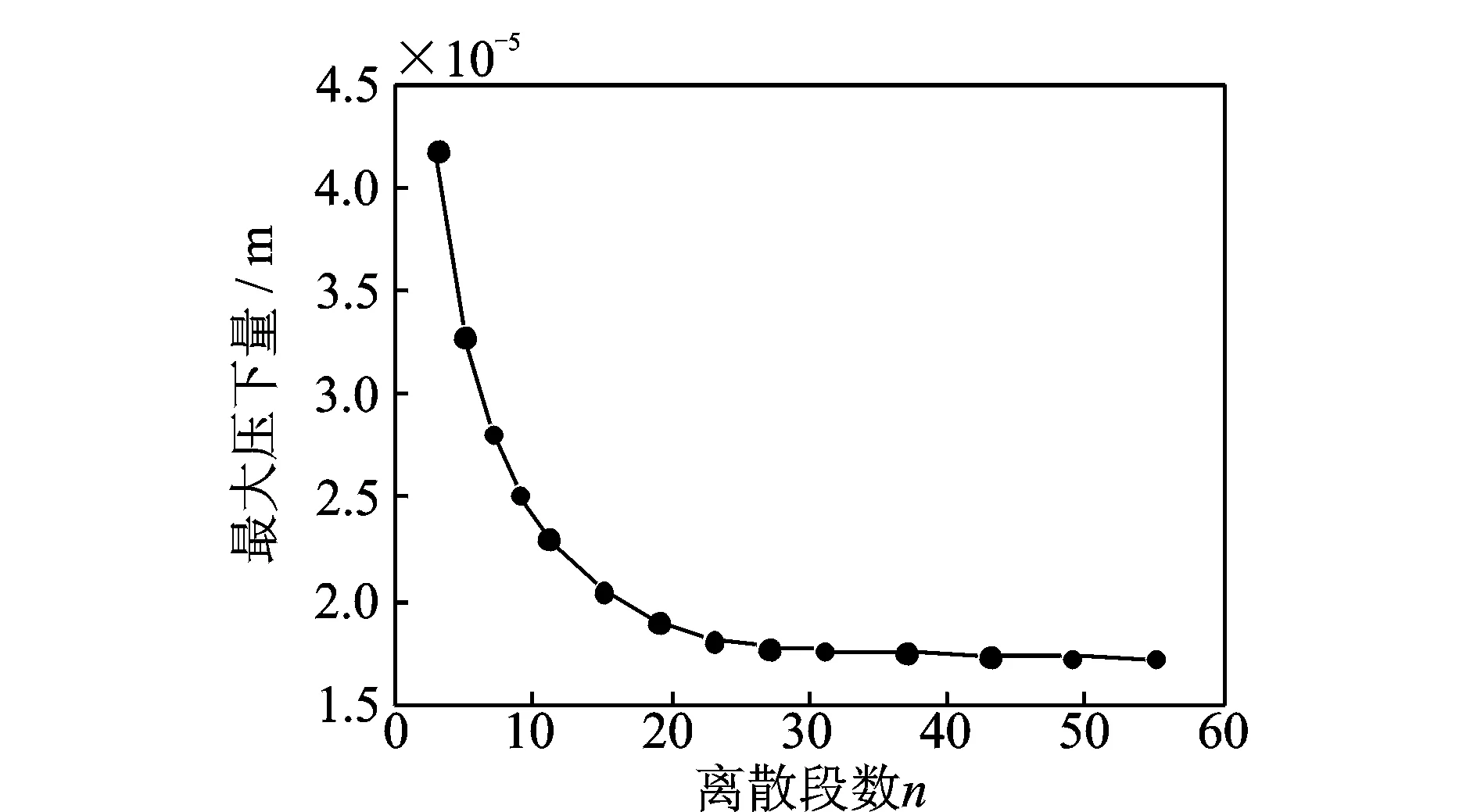
图4　不同离散密度下计算得到的法向最大压下量Fig.4　The maximum normal penetration under different discretized segments

3.2结果验证

(1)实际实验对比

为验证本文模型的计算精度，本节依照表1给出的2组实验初始条件(摩擦系数为μ=0.075，恢复系数e*=1)采用本文方法进行数值计算，并将本文结果与实验结果[18]进行对比。

表1　两组实验的初始条件

Tab.1　Initial conditions of two groups of experiment

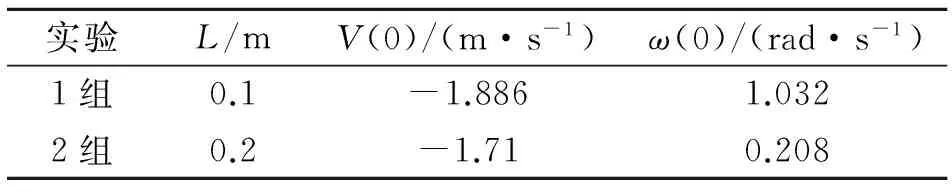
实验L/mV(0)/(m·s-1)ω(0)/(rad·s-1)1组0.1-1.8861.0322组0.2-1.710.208

由于实验给出的初始条件满足初始黏滞条件(17)，所以接触点的初始运动状态为黏滞压缩。图5为分离时刻杆端的接触点切向速度混合模型解和实验数据。通过比较表明，数值结果与实验结果基本吻合。二者之间误差产生的主要原因可能是HAM模型是一维梁且在平面内运动，而实验则是一个真实三维梁以一个初始角度自由落体运动。且与静力学实验相比，接触动力学实验结果数据本身离散性也较大。此外，经计算除了当u0(0)=π/2时，接触点运动模式为黏滞压缩-滑动压缩，其余角度值下接触点的运动模式均为黏滞压缩-滑动压缩-滑动恢复。

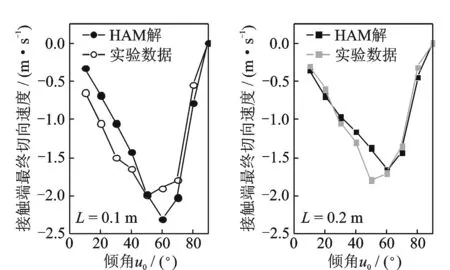
图5　接触端接触结束时切向速度Fig.5　Tangential velocity of the contact point at the end of contact

(2)数值实验对比

由于真实的实验环境能够获得的实验数据有限，为进一步地验证本文混合分析模型的精度，将本文模型的结果与非线性商业有限元的仿真结果进行对比。在商业有限元Ls-Dyna模拟中，本着疏密有致的离散原则，为了满足非线性迭代接触算法以及更好地捕捉接触响应，对接触区实施了网格细化(如图6所示)，显然这样会增加自由度，降低计算效率。

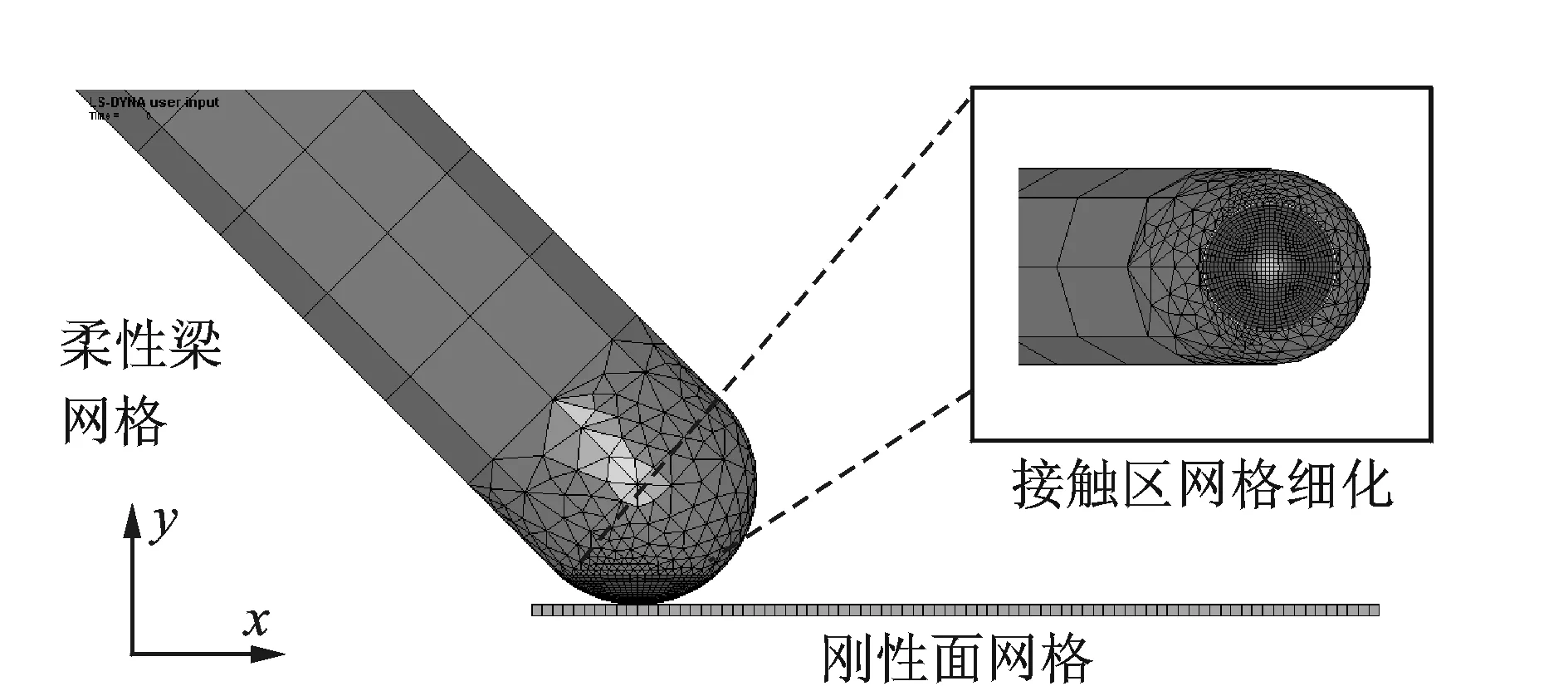
图6　梁与刚性平面弹性碰撞的有限元离散模型Fig.6　Finite element model for bar oblique impacts on rigid half-space

图7是不同摩擦系数μ下的法向和切向接触力时程曲线。计算结果表明，本文的方法与FEM方法获得的接触力响应所得的峰值、接触时间以及曲线的变化形式吻合较好，接触力峰值误差仅为12%。二者之间误差产生的原因主要是FEM模型是一个三维梁模型，由于泊松效应梁会产生横向变形，同时杆件也容易产生横向运动。从图7～9可以看出，当μ=2/3时，系统的运动模式依次为滑动压缩-滑动恢复-分离，切向没有经历黏滞运动；当摩擦系数变大，即当μ=5/3和μ=8/3时，系统的运动情况由滑动压缩-黏滞压缩-黏滞恢复-反向滑动恢复-分离构成，在接触面切向经历了滑动-黏滞-反向滑动的3个运动状态的转换。当μ=5/3和μ=8/3时(此摩擦系数恰好处于刚体斜碰撞模型中的经典painlevé悖论区[14])，法向接触力响应和切向接触力响应的峰值几乎相等，即当摩擦系数超过5/3时，接触力的峰值保持不变。这与完全刚体模型的摩擦显著不同，造成这个现象的原因正是由于考虑了切向接触柔度和存在切向黏滞运动。分析还发现纯滑动时接触力的峰值明显小于具有黏滞状态的接触力的峰值。

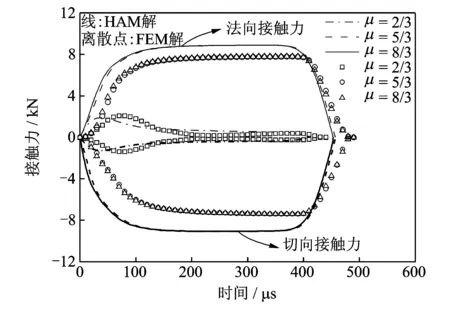
图7　切向和法向接触力(-V1(0)/V3(0)=3.5，u0=3π/4，η2=1.21, e*=1)Fig.7　Normal and tangential components of contact force during oblique impact of a beam against a rough half-space (-V1(0)/V3(0)=3.5，u0=3π/4，η2=1.21, e*=1)

图8和9分别为不同摩擦系数μ下接触点的法向和切向相对速度响应。图中的商业有限元解选择接触区中心的单元的速度。当摩擦系数相同时，二者的曲线基本一致，误差较小(例如，接触时间误差仅为5.6%)，说明本文给出的混合分析模型是合理有效的。分析图8发现，摩擦系数对分离时刻接触点的法向速度有着重要影响。摩擦系数越大，接触点的法向速度的最小值越小。分析还发现，无论摩擦系数多大，接触点C的法向速度的响应曲线在接触发生不久总存在震荡现象。当μ=5/3和μ=8/3时，接触点的法向速度在初始阶段减小，即法向加速度在接触开始的一段时间内出现负值，使得法向速度出现负向增加，导致系统的切向摩擦力变大，若采用完全刚性体模型进行分析，此时会出现经典的Painlevé悖论现象。分析图9发现，当μ=2/3时，C点切向速度增加，始终大于初始速度。但当μ=5/3和μ=8/3时，C点切向速度随时间的推移发生降低，然后反向滑动增加。

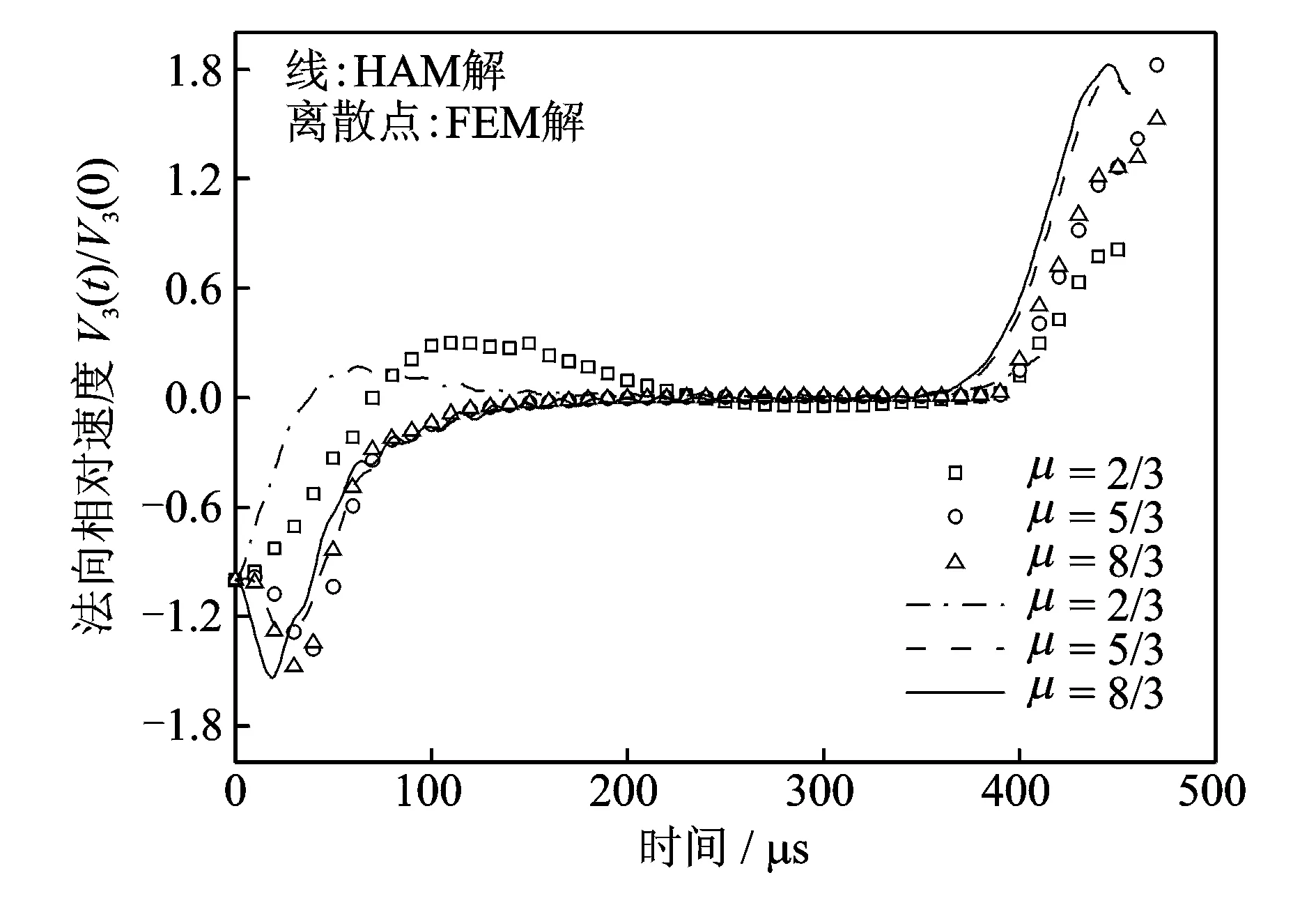
图8　接触点C和C′法向无量纲相对速度(-V1(0)/V3(0)=3.5, u0=3π/4,η2=1.21,e*=1)Fig.8　Normal relative non-dimensional velocity between C and C′ (-V1(0)/V3(0)=3.5, u0=3π/4, η2=1.21, e*=1)

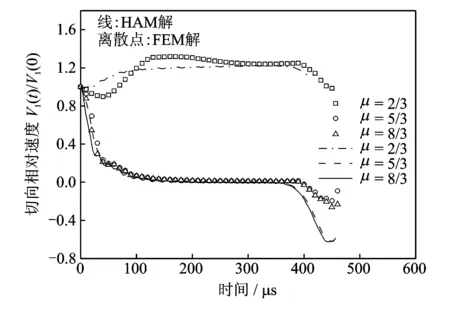
图9　接触点C和C′的切向无量纲相对速度(-V1(0)/V3(0)=3.5,u0=3π/4,η2=1.21,e*=1)Fig.9　Tangential relative non-dimensional velocity between C and C′ (-V1(0)/V3(0)=3.5, u0=3π/4, η2=1.21, e*=1)

4　结　论

本文提出采用混合分析模型研究柔性梁摩擦斜碰撞问题，利用事件驱动法深入研究了整个接触过程中的切向黏滑状态和法向压缩恢复阶段的反复切换。将HAM模型的计算结果与实验结果以及商业有限元方法进行了对比，研究得到了以下主要结论：

(1) 本文混合模型解与实验数据吻合较好，验证了该模型具有较好的收敛性和较高的精度。由于考虑了接触区切向柔度，该模型具备了分析一系列切向黏-(反向)滑运动模式的能力。

(2) 研究表明：结构的整体柔度和接触区的切向接触柔度会对接触力响应和接触点的切向黏滑运动模式带来较大的影响。

(3) 由于引入了能量恢复系数，因此混合模型可考虑接触区弹塑性变形导致的碰撞能量的损失。

[1]Elkins-Tanton L T. Evolutionary dichotomy for rocky planets [J]. Nature, 2013, 497: 570—572.

[2]Popov V L. Contact Mechanics and Friction: Physical Principles and Applications [M]. Berlin University of Technology, 2010.

[3]Hayne P O, Greenhagen B T, Foote M C, et al. Diviner lunar radiometer observations of the LCROSS impact [J]. Science, 2010, 330: 477—479.

[4]Humphery J A C. Fundamentals of fluid motion in erosion by solid particle impact [J]. International Journal of Heat and Fluid Flow, 1990, 11(3): 170—195.

[5]Chapnik B V, Heppler G R, Aplevich J D. Modeling impact on a one-link flexible robotic arm [J]. IEEE Transaction on Robotic and Automation, 1991, 7(4): 551—561.

[6]张锁怀，沈允文，董海军，等. 齿轮拍击系统的动力响应[J]. 振动工程学报, 2003, 16(1)：62—66.

ZHANG Suohuai, SHEN Yunwen, DONG Haijun, et al. Dynamic response of a gear rattling system [J]. Journal of Vibration Engineering, 2003, 16(1)：62—66.

[7]李晓杰，莫非，闫鸿浩，等. 爆炸焊接斜碰撞过程的数值模拟[J]. 高压物理学报, 2011, 25(2)：173—176.

Li Xiaojie, Mo Fei, Yan Honghao, et al. Numerical simulation of the oblique collision in explosive welding [J]. Chinese Journal of High Pressure Physics, 2011, 25(2): 173—176.

[8]徐从启，谢旭辉，戴一帆. 摩擦接触约束下的微小管道机器人管内运动稳定性分析[J]. 机械工程学报, 2010, 46(15)：36—44.

Xu Congqi, Xie Xuhui, Dai Yifan. Motion stability analysis of micro in-pipe robot with frictional contacts [J]. Journal of Mechanical Engineering, 2010, 46(15): 36—44.

[9]段洁，丁千. 三质体斜碰撞振动的动力学和减振研究[J]. 振动工程学报, 2013, 26(1)：68—74.

DUAN Jie, DING Qian. Dynamics and vibration reduction of three-mass system with oblique-imapcts [J]. Journal of Vibration Engineering, 2003, 16(1)：62—66.

[10]Han W, Jin D P, Hu H Y. Dynamics of an oblique-impact vibrating system of two degrees of freedom[J]. Journal of Sound and Vibration, 2004, 275(3-5): 795—822.

[11]Han W, Hu H Y, Jin D P. Experimental study on dynamics of an oblique-impact vibrating system of two degrees of freedom[J]. Nonlinear Dynamics, 2007, 50(3): 551—573.

[12]Xie J H, Ding W C. Hopf-Hopf bifurcation and invariant torus T2of a vibro-impact system[J]. International Journal of Non-linear Mechanics, 2005, 40: 531—543.

[13]彼得.艾伯哈特，胡斌. 现代接触动力学[M]. 南京:东南大学出版社, 2003.

Eberhart P, Hu B. Modern Contact Dynamics [M]. Nanjing: Southeast University Press, 2003.

[14]Shen Y, Stronge W J. Painlevé Paradox during oblique impact with friction[J]. European Journal of Mechanics A/Solids, 2011, 30(4): 457—467.

[15]Johnson K L. The bounce of ‘super ball’[J]. International Journal of Mechanical Engineering,1983,111: 57—63.

[16]Stronge W J. Impact Mechanics[M]. Cambridge University Press. 2000.

[17]Stoianovici D, Hurmuzlu Y. A critical study of the applicability of rigid body collision theory[J]. ASME Journal of Applied Mechanics, 1996, 63(2): 307—316.

[18]Hurmuzlu Y. An energy based coefficient of restitution for planar impacts of slender bars with massive[J]. ASME Journal of Applied Mechanics, 1996, 65(4): 952—962.

Research on rigid body-spring-particle hybrid model for flexible beam under oblique impact with friction

SHENYu-nian,GUJin-hong

(Department of Mechanics and Engineering Science, Nanjing University of Science and Technology， Nanjing 210094， China)

In order to quickly and accurately estimate the complex transient behavior of oblique collision with friction, a hybrid analysis model (HAM) is presented in this paper. This model takes account of the normal contact compliance, the tangential contact compliance of the local contact zone and the global compliance of the beam altogether. Based on the finite segment theory, the displacement field of the non-contact zone of the beam is discretized into a spring-damper-rigid body system. The bilinear process of normal compression-restitution deformation and the tangential deformation process of the local contact zone are described by an elastic-plastic spring-particle system with energy coefficient of restitution. The dynamic equations of the HAM which are piecewisely continuous under different contact states are derived. According to the switching criterion between compression and restitution as well as stick and slip, numerical examples are solved by the event-driven method. Through comparison of the results with the experimental data and those obtained by the commercial finite element software, it is shown that the hybrid model can accurately estimate the time history of contact forces and describe the repeatedly transition between stick and slip motion, which validate the applicablity of HAM.

nonlinear vibration; oblique impact; tangential compliance; frictional contact; stick-slip motion

2014-04-25；

2015-09-21

国家自然科学基金资助项目(11302107，11572157，11372138)；高等学校博士学科点专项科研基金资助项目(20123219120042)

O322; O313.4

A

1004-4523(2016)01-0001-07

10.16385/j.cnki.issn.1004-4523.2016.01.001

沈煜年(1982—),男,副教授。电话:(025)84315590; E-mail:shenyunian@aliyun.com