混合FE-SEA线连接建模方法研究*
2016-09-29朱卫红马兴瑞韩增尧邹元杰
朱卫红, 马兴瑞, 韩增尧, 邹元杰
(1.中国空间技术研究院,北京 100094; 2.中国国家航天局,北京 100048)
混合FE-SEA线连接建模方法研究*
朱卫红1, 马兴瑞2, 韩增尧1, 邹元杰1
(1.中国空间技术研究院,北京 100094; 2.中国国家航天局,北京 100048)
基于傅里叶变换提出了一种混合FE-SEA线连接建模方法。首先基于波动理论推导了波数空间下的板结构线连接的阻抗矩阵,然后针对线连接位移构造了一种节点坐标系下三角波形函数,最后依据傅里叶变换技术建立了节点坐标系下的线连接模型。仿真算例分析结果表明,该混合线连接建模方法具有较好的精度,能够有效地建立线连接的动力学特性建模。
线连接; 航天器; 力学环境预示; 形函数; 混合FE-SEA
引 言
航天器结构的中高频的动力学响应预示是比较困难的,是目前国内外研究的难点和热点[1]。中频段的动力学特性预示困难,主要是由于在该频段航天器各子结构或子系统的动力学特性差异很大,很难用常规的有限元方法(Finite Element Method, FEM)或统计能量分析(Statistical Energy Analysis, SEA)解决[2]。为了解决该类力学环境预示问题,混合有限元-统计能量分析方法(Hybrid Finite Element-Statistic Energy Analysis)[3-4]得到了国内外学者和工程师的关注,已逐渐应用于航天航空领域[5-7]。该方法首先将系统进行划分:波长大于特征尺寸的子系统,划分为确定性子系统,采用有限元建模;波长小于特征尺寸的子系统,划分为随机子系统,采用统计能量子系统建模。确定性子系统和随机子系统由混合连接边界上的直接场和混响场的互易关系耦合[8],然后求解得到整体系统的响应,因此混合有限元-统计能量方法的核心在于混合连接的建模。
混合连接有多种连接方式,包括点、线、面等不同形式。其中,针对点连接的理论研究较多[9],公开资料也比较全,但对于更加常见和普遍的线连接的研究却刚刚起步,国内相关理论并不完善,可查阅的资料不多。事实上,航天器结构中线连接比较普遍,如星体壁板的交界处和卫星与火箭的对接界面。如果线连接的两类结构刚度差异大,就可一部分采用有限元建模,而另一部分采用统计能量建模。这种情况就是典型的有限元-统计能量分析的线连接形式。本文基于波动理论,首先推导了波数空间下的线连接阻抗特性,构造了一种线性插值三角波形函数描述线连接处的位移,采用傅里叶变换技术得到了节点坐标系下的线连接模型。算例仿真分析表明,本文提出的建模方法是有效的,具有一定的理论研究价值和工程应用价值。
1 波数空间下的线连接动力学方程
1.1混合FE-SEA基本理论
混合FE-SEA方法理论认为随机子系统的能量由直接场和混响场两部分能量组成。直接场能量定义为通过连接输入到子系统后未经过任何边界反射的能量,混响场能量为经过多次反射后的能量,如图1所示。
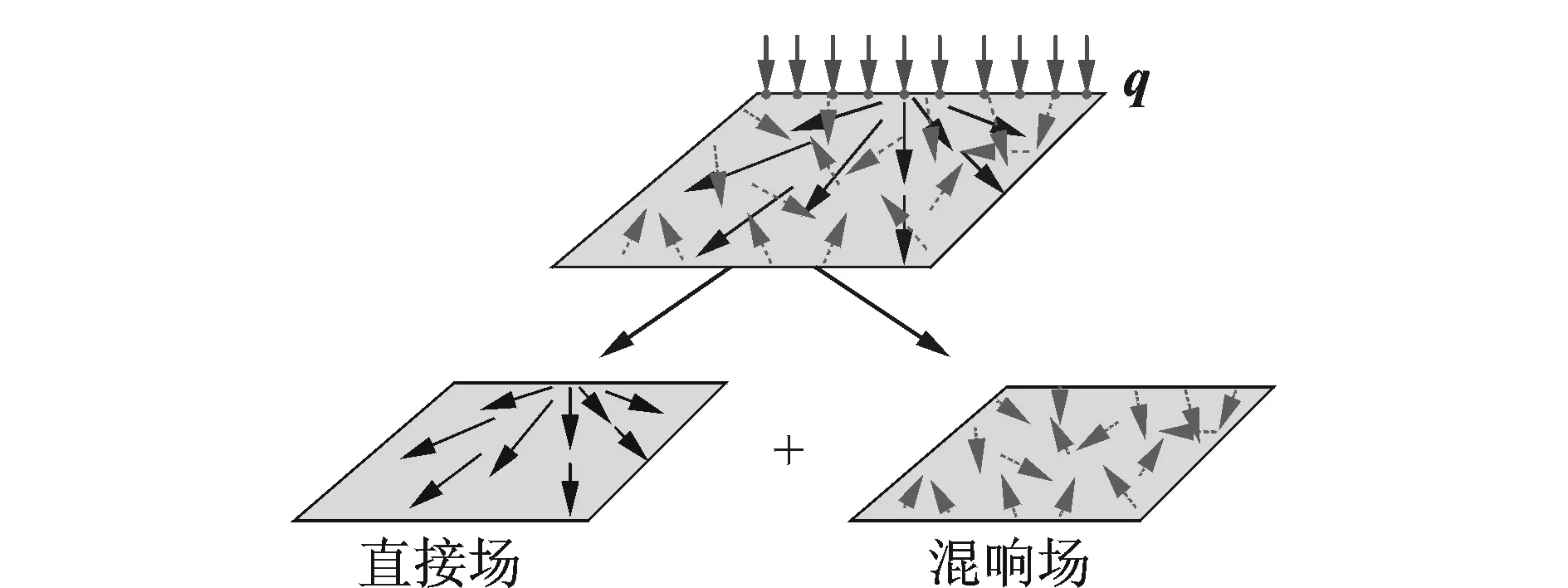
图1 直接场和混响场Fig.1 The direct field and reverberant field
假设随机子系统与有限元的混合连接边界的自由度为q,则随机子系统的动力学响应可表示为
(1)
式中frev为随机子系统混响场在混合连接边界处产生的受挡混响力,f为外载荷,Ddir为混合连接的直接场动刚度矩阵。混响场的响应一般为能量,由直接场与混响场的互易关系可建立受挡混响力和混响场能量的转换关系[8]
(2)
式(2)是混合FE-SEA方程的核心,可以看出连接的建模关键在于连接的直接场动刚度矩阵,因此混合连接的建模主要围绕连接的直接场动刚度矩阵展开。
1.2波数空间下线连接的动力学方程
板类子系统以横向运动为主要运动,由于弯曲波通常远小于拉伸和剪切波,所以面外运动通常采用统计能量子系统建模,而面内运动在分析时忽略或者采用有限元进行建模。为了节省篇幅,本文仅仅建立了线连接的面外运动的动力学方程。图2为由n块板组成线连接示意图,能量通过线连接以不同形式的波向结构辐射能量。

图2 线连接示意图Fig.2 The schematic diagram of line junction
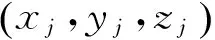
(3)
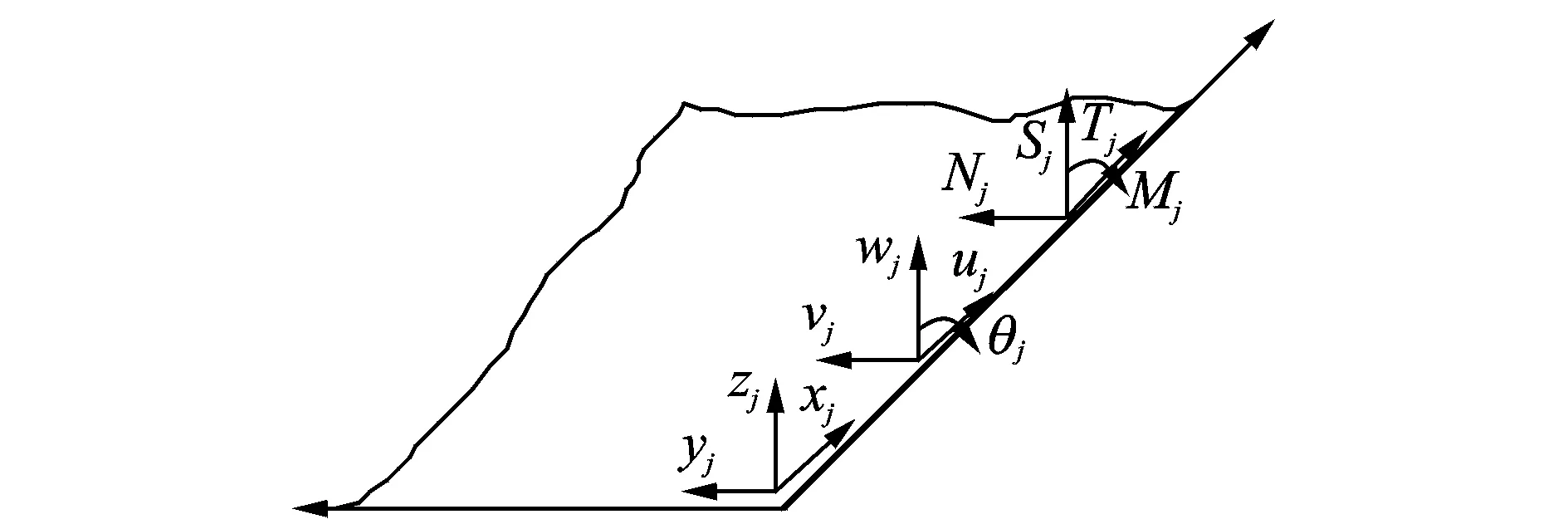
图3 线连接的局部坐标系Fig.3 The local coordinate of line junction
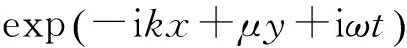
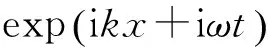
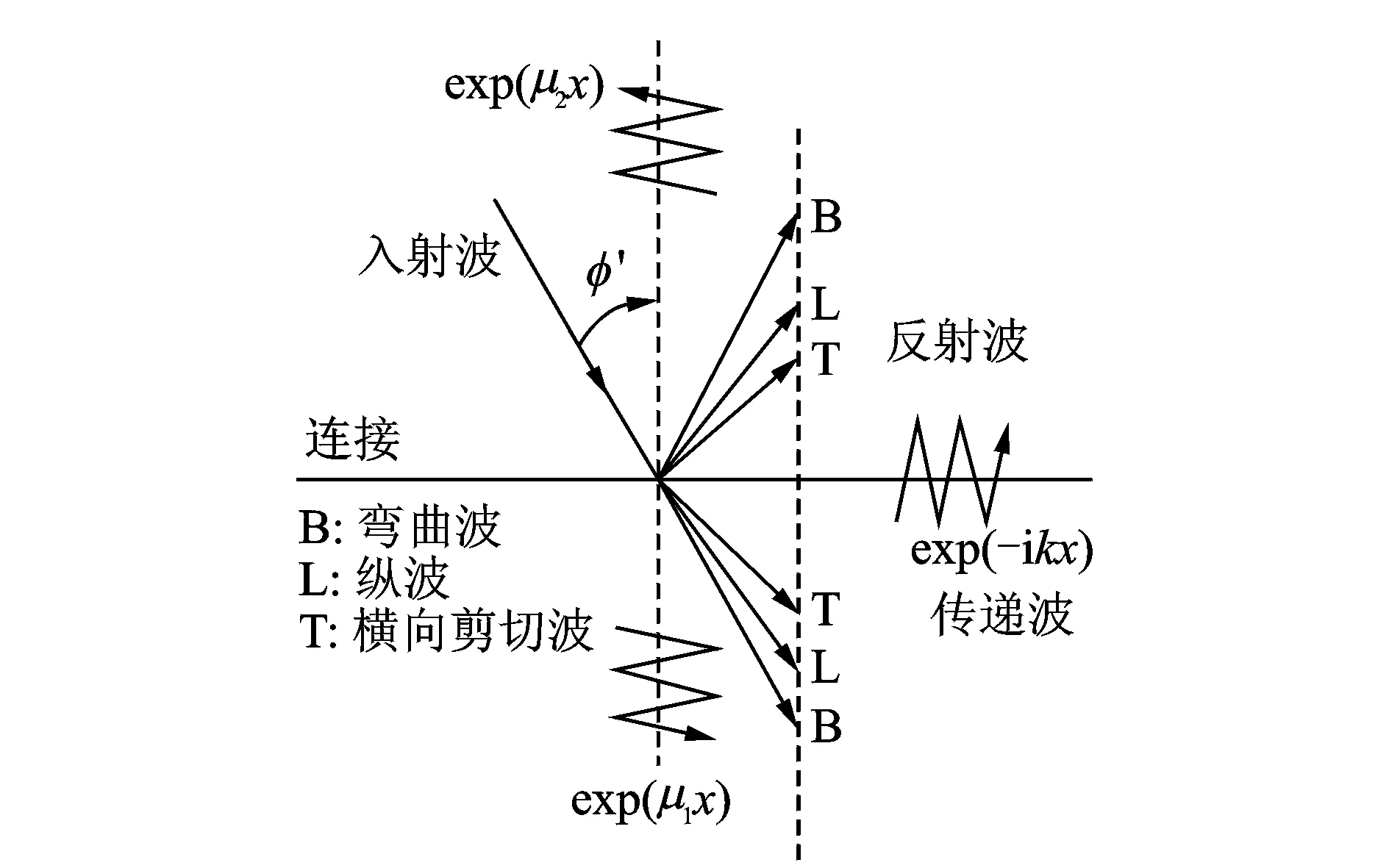
图4 连接处波传播的Snell定理示意图Fig.4 The Snell theory of wave transmission at the junction
(4)
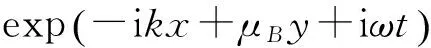
(5)
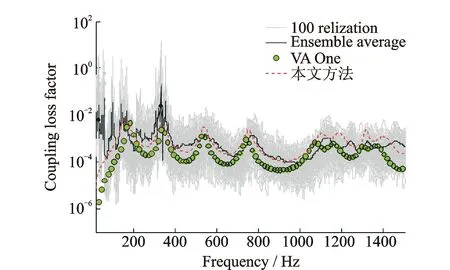
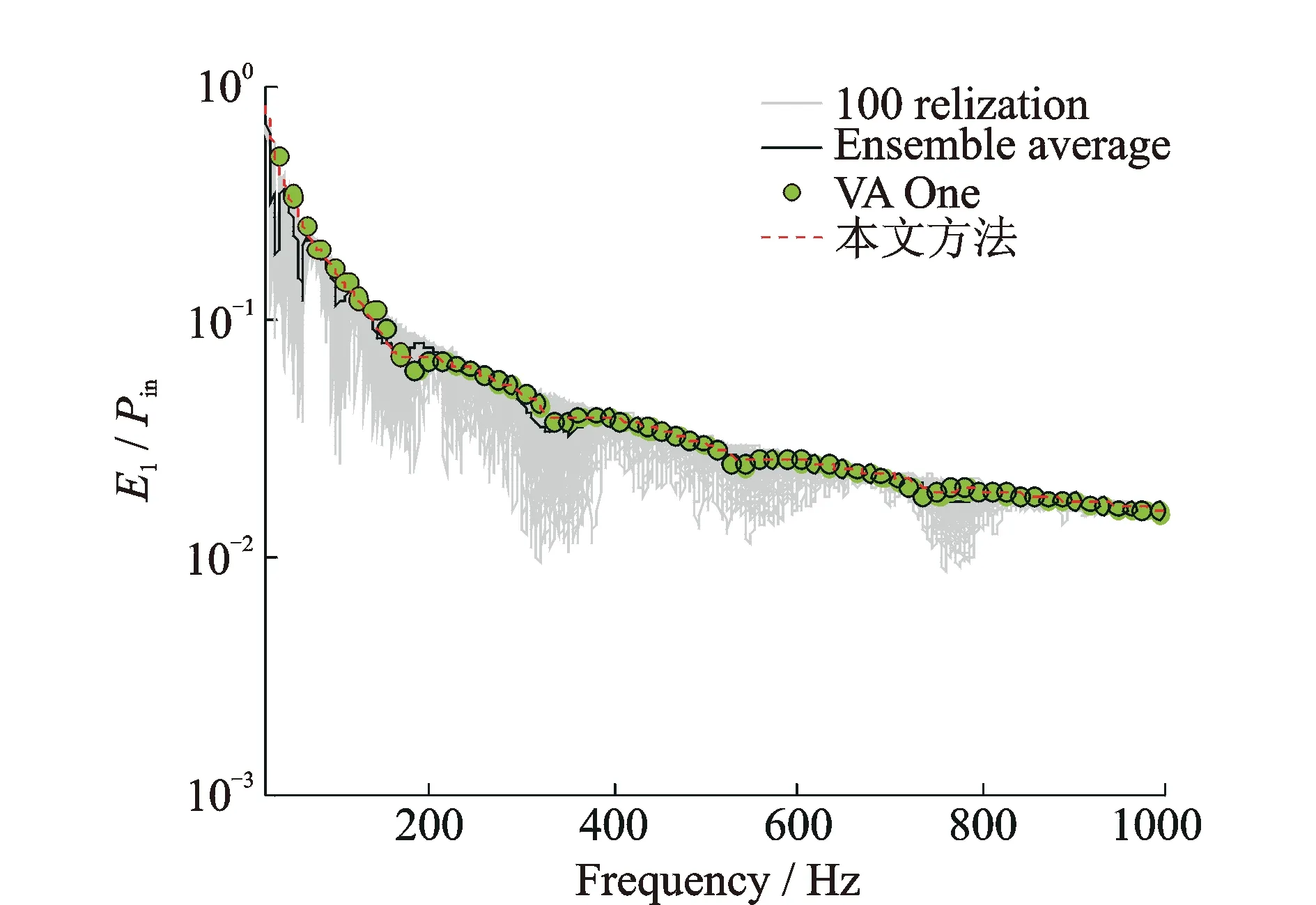
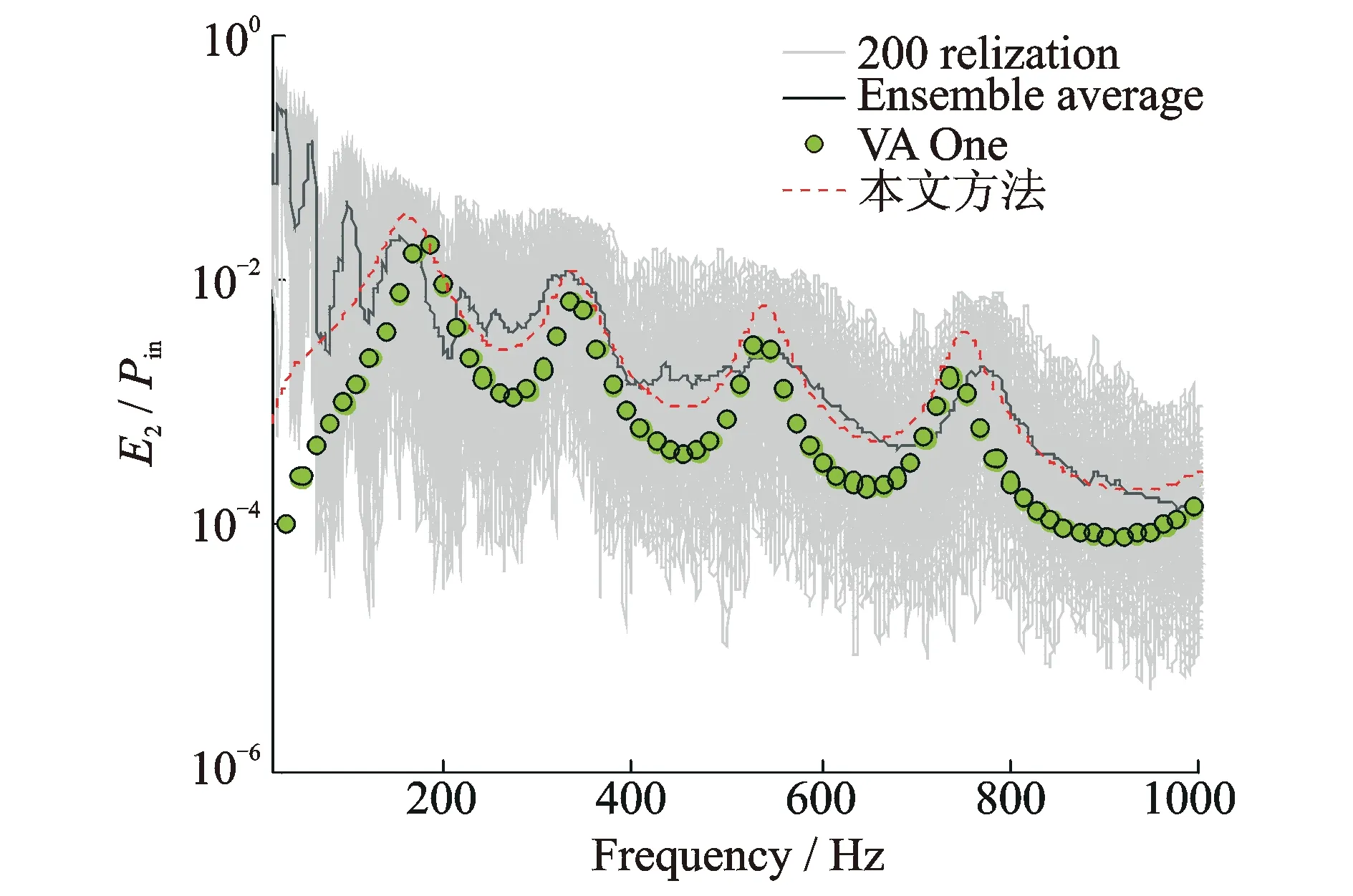
式中kB为弯曲波数。y方向的波数可由方程(5)确定。由方程(5)可得4个根,其中负虚根和负实根是符合真实状况的波数,可以描述正y方向波的传递和衰减。实际上当k≥kB时,μB取2个负实数,此时y方向的波为近场衰减波,不传递能量;当k (6) (7) 考虑边界处y=0,结合方程(6)和(7)有,则有 (8) (9) (10) 由经典薄板理论可得x轴向力矩和横向力可表示为: (11) (12) 式中υ为板结构的泊松比, 将式(6)代入式(11)和(12)得: (13) (14) 将式(13)和(14)代入式(9)和(10)得 (15) (16) 2.1基于傅里叶变换的动力学方程坐标变换 上述动力学方程是基于波数空间坐标系建立的,因此需要通过傅里叶变换获得节点坐标系下的线连接直接场动刚度矩阵[11]。 (17) (18) 将该载荷投影在广义坐标am上,则相应的广义力可表示为 (19) 将式(18)代入式(17)可得 (20) 定义线连接处的动刚度为 (21) 则 (22) (23) (24) (25) 2.2基于线性插值的三角波形函数 为了描述节点的位移,首先必须构造节点的位移形函数,本文采用由线性插值获得的三角波形函数,如图5所示。 图5 线连接的位移形函数Fig.5 The displacement shape function of line junction 若线连接处的横向位移w(或θ)可描述为 (26) (27) 图6 形函数示意图Fig.6 The schematic diagram of triangle wave shape function 式中Δl为节点间的距离。考察节点位于x=0处的形函数,其波数空间下的傅里叶变换可表示为 (28) (29) 采用上面形函数建立板的面外运动,其位移可表示为 (30) 将形函数代入即可得到节点坐标系下的线连接直接场动刚度矩阵 (31) 为了验证本文提出的线连接模型的有效性,对如图7所示的结构进行仿真验证。结构由2块相同的板结构和复杂的连接组成。板结构为铝合金,连接结构为钢,具体几何参数如表1所示。分析频率范围为1~1000 Hz,点载荷施加在其中一个SEA板子系统上。考虑到整个系统的动力学特性,模态密度较大的板面外位移采用SEA建模,模态密度小的板的面内位移和刚度大的复杂连接采用FEM建模,2种模型通过2个混合线连接耦合,如图8所示。 图7 组合结构模型Fig.7 The model of combined structures 参考算法采用基于有限元的能量流分析与Monte Carlo试验相结合的方法[12],并与商业软件VA One[13]的计算结果进行对比。有限元方法是目前广泛应用的一种动力学分析方法,通过对分析数据或者算法进行二次开发实现子系统的能量流分析,同时采用Monte Carlo仿真引入参数摄动描述不确定性对中高频响应的影响。由于有限元方法并未使用大量的假设,能量流分析-Monte Carlo仿真方法的分析结果可作为SEA方法或中频力学环境预示方法研究和改进的依据[3,14-16]。 图9为2个统计能量子系统间的耦合损耗因子计算结果。仿真结果表明,本文提出的建模方法和VA One的计算结果均与Monte Carlo仿真的结果都相吻合。但是VA One计算结果偏于保守,尤其是在非共振峰位置。 图9 板1和板2间的耦合损耗因子Fig.9 The coupling loss factor between plate 1 and plate 2 图10和图11分别为统计能量子系统的能量响应。可以看出3种方法计算得到的板1的能量非常吻合,但是VA One计算得到的板2的能量偏于保守,尤其是在非共振峰位置。图12给出了板2的能量的相对误差,参考结果为Monte Carlo试验结果(0 dB)。分析结果显示在250~500 Hz,VA One误差比本文方法误差平均大3 dB,VA One最大误差6.77 dB,本文方法最大误差3.16 dB。而在600~1000 Hz之间,在共振峰位置本文方法与VA One的误差相差1 dB左右,而在非共振峰位置,VA One最大误差比本文方法大7 dB左右。本算例仿真表明,本文提出的建模方法能够有效地建立板结构面外运动的线连接模型,Monte Carlo试验表明,本文方法具有较好的预示精度,尤其是在非共振峰位置,精度优于VA One,同时共振峰位置也能保证相对高的精度。 总体而言,本文方法与VA One的混合线连接模型均能有效地描述能量在连接处的传递,但是在某些频段VA One偏于保守,导致上述差异的原因在于:一方面VA One采用的混合线连接建模方法及位移形函数模型可能与本文方法有所不同;另一方面由于衰减波不传递能量,本文没有考虑衰减波对混响场的能量贡献,而VA One在建模过程中考虑了衰减波对混响场的能量贡献,这也是导致二者差异的原因之一,后续应当进一步展开衰减波对线连接建模与分析结果的影响研究。 图10 板1的能量Fig.10 The energy of plate 1 图11 板2的能量Fig.11 The energy of plate 2 图12 板2的能量误差曲线Fig.12 The error curve of plate 2 energy 本文研究了一种基于傅里叶变换技术的混合线连接建模方法。该方法基于由波动理论得到的线连接阻抗矩阵,通过构造线性插值三角波形函数,采用波数空间下的傅里叶变换技术得到节点坐标系下的线连接模型。仿真结果表明,本文提出的线连接建模方法具有比较好的分析精度,能够预示能量在线连接处的传递,可应用于航天器的中频段动力学环境预示,具有一定的理论研究和工程应用价值。 [1]邹元杰,韩增尧,张瑾.航天器全频域力学环境预示技术研究进展[J].力学进展,2012,42(4):445—454. Zou Yuanjie, Han Zengyao, Zhang Jin. Research progress on full-frequency predication techniques of spacecraft’s mechanical environment[J]. Advances in Mechanics,2012,42(4):445—454. [2]Shorter P J, Gardner B K, Bermner P G. A hybrid method for full spectrum noise and vibration prediction[J]. Journal of Computational Acoustics,2003,11(2):323—338. [3]Shorter P J, Langley R S. Vibro-acoustic analysis of complex systems[J]. Journal of Sound and Vibration, 2005,288(3): 669—699. [4]朱卫红,马兴瑞,韩增尧.航天器中频力学环境预示技术研究进展[J].航天器工程,2014,23(1):110—117. Zhu Weihong, Ma Xingrui, Han Zengyao. Reasearch evolution on mid-frequency mechanical environment predication of spacecraft[J]. Spacecraft Enginneering, 2014,23(1): 110—117. [5]Jeffrey M Larko, Cotoni V. Vibroacoustic response of the NASA ACTS spacecraft antenna to launch acoustic excitation[R]. Washington D C,Glenn Research Center, NASA/TM—2008-215168,2008:1—15. [6]Chen S M, Wang D F, Zan J M. Interior noise prediction of the automobile based on hybrid FE-SEA method[J]. Mathmatical Problems in Engineering, 2011, 2011(4) :1—20. [7]Prasanth S, Charpentier A, Fukui K. Using the hybrid FE-SEA model of a trimmed full vehicle to reduce structure born noise from 200Hz to 1 kHz[C]. 12th Symposiumon International Automotive Technology,2011, Pune, India, 2011: 25959—25967. [8]Shorter P J, Langley R S. On the reciprocity relationship between direct field radiation and diffuse reverberant loading[J]. The Journal of the Acoustic Society of America, 2005, 117(1):85—95. [9]张瑾. FE-SEA方法在航天器力学环境预示中的应用研究[D].北京:中国空间技术研究院,2011. Zhang Jin. Spacecraft mid-frequency dynamic prediction using FE-SEA hybrid method[D]. Beijing: China Acadamy of Space Technology, 2011. [10]Langley R S, Heron K H. Elastic wave transmission through palte/beam junction[J]. Journal of Sound and Vibrtion,1990,143(2):241—253. [11]Cotoni V, Shorter P. Numerical and experimental validation of a hybrid finite element-statistical energy analysis method[J]. The Journal of the Acoustic Society of America,2007,122(1):259—270. [12]Mace B R, Shorter P J. Energy flow models from finite element analysis[J]. Journal of Sound and Vibration, 2000, 233(3):369—389. [13]ESI Group. VA One 2010.5 User’s Guide[Z]. Paris: ESI Group, 2010. [14]Gardner B, Shorter P J, Cotoni V. Vibro-acoustic analysis of large space structures using the hybrid FE-SEA method[C]. 46th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics & Materials Conference, Austin, Texas, 2005, 1—11. [15]Contoni V, Shorter P J, Langley R S. Numerical and experimental validation of a hybrid finite element-statistical energy analysis method[J].Journal of the Acoustic Society of America, 2007, 12(1): 259—270. [16]Langley R S, Cordioli J A. Hybrid deterministic-statistical analysis of vibro-acoustic systems with domain coupling on statistical components[J]. Journal of Sound and Vibration, 2009, 321(1):893—912. The research on the modeling method of hybrid FE-SEA line junction ZHUWei-hong1,MAXing-rui2,HANZeng-yao1,ZOUYuan-jie1 (1. China Academy of Space Technology, Beijing 100094, China;2. China National Space Administration, Beijing 100048, China) A modeling method of hybrid line junction is proposed based on the Fourier transform. Firstly, the impedance matrix of plate line junction is deduced with the wave theory.Then a triangular wave shape function of line junction displacement is constituted in the node coordinate system. Finally the hybrid line junction model in node coordinate is established using the Fourier transform algorithm. The analysis of numerical example shows that the method proposed in this paper has a good precision, and can model the dynamic characteristics of line junction effectively. line junction; space craft; mechanical environment predication; shape function; hybrid FE-SEA 2014-04-11; 2015-05-04 总装“十二五”预研项目(51334050101)和国防973项目(613133) TB123; V414.4 A 1004-4523(2016)01-0017-07 10.16385/j.cnki.issn.1004-4523.2016.01.003 朱卫红(1985—),男,博士研究生。电话:13810273147;E-mail:zhuweihong-2004@163.com
2 节点坐标系下的直接场动刚度矩阵及形函数的构造
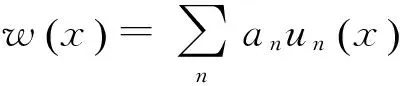

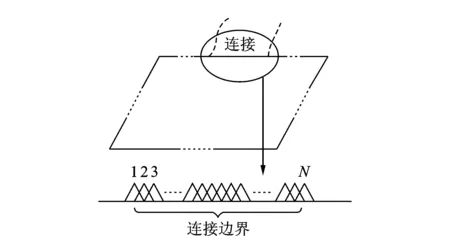
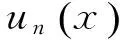
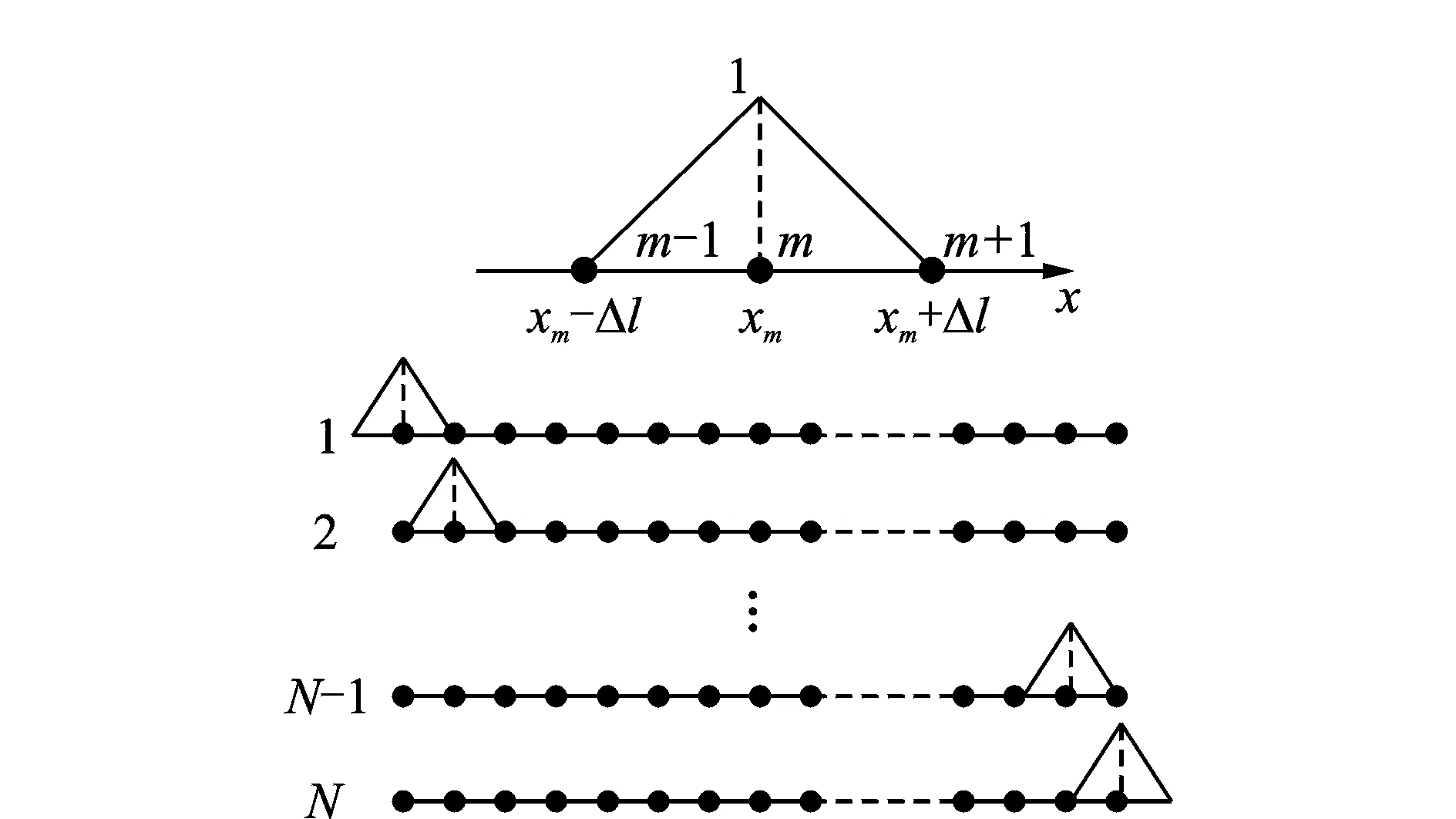
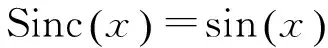
3 仿真算例


4 结 论
