均匀来流下方柱表面风压非高斯特性的流场机理

杜晓庆，靳晓雨，许汉林，刘延泰

（1.上海大学土木工程系，上海200072；2.上海大学风工程和气动控制研究中心，上海200072）

对于建筑主体和围护结构而言，研究人员往往最关注的是结构表面的极值风荷载和风压非高斯特性，并用极值风压验算局部结构的安全性。而传统的分析方法是将作用在结构上的风荷载假设为高斯随机过程。研究［1-4］表明：建筑局部表面存在明显的风压非高斯特性，极值风压使结构更容易发生疲劳破坏，但风压非高斯特性的形成机理尚未澄清。因此，澄清方柱表面风压非高斯特性的产生机理不仅有利于理解超高层建筑的风荷载特性，也有助于对其提出新的气动控制措施。

矩形截面在超高层建筑中应用广泛，韩宁等［5］和庄翔等［6］通过风洞试验对方形建筑和矩形建筑的风压非高斯特性进行了研究，结果表明：建筑表面的风压偏度和峰度均随风向角会发生明显的变化，建筑背风面是主要的风压非高斯区域。楼文娟等［7］也通过风洞试验研究了带切角的菱形超高层建筑的风压非高斯特性，发现侧面前缘分离区、背风面及迎风面切角区域存在显著的风压非高斯特性，并给出了风压非高斯区域的划分依据。除了超高层建筑外，风压的非高斯特性也是大跨度屋盖［8］和冷却塔等［9］抗风设计重点关注问题之一。但受到风洞试验条件的限制，以往研究均未从流场角度给出极值风压的产生机理和风压非高斯特性的形成机理。

均匀来流作用下的二维方柱（无限长方柱）是方形截面超高层建筑的简化模型，研究二维方柱极值风压和风压非高斯特性的形成机理有助于理解超高层建筑的抗风性能。以往文献［10-13］对方柱的气动性能和流场特性随风向角的变化进行了广泛研究，并根据不同风向角将方柱绕流场分成3种流态，即：①小风向角（α=0°～10.0°），为“前角分离流态”；②中风向角（α=10.0°～30.0°），为“分离泡流态”；③大风向角（α=30.0°～45.0°），为“附着流流态”，但尚未见到采用数值模拟方法系统研究方柱风压非高斯特性流场机理的文献。

本文针对均匀来流作用下的二维方柱，采用大涡模拟方法，在雷诺数为22 000的条件下，研究方柱表面风压非高斯特性随风向角的变化规律，分析风压非高斯区域与平均流场的关系，并基于瞬时流场结构探究方柱表面风压非高斯特性和极值风压的形成机理。

1 计算模型及验证

图1为计算模型示意图，来流风速U0为3.28m·s-1，方柱边长D为0.1m，风向角为α=0°～45.0°，雷诺数Re=2.2×104，图中CL为方柱平均升力系数、CD为方柱平均阻力系数。图2为计算域及边界条件，入口边界距离方柱中心为20D，方柱中心距离出口边界为30D，横风向计算域为40D，展向高度为2D，阻塞率为2.5%。计算域边界条件采用均匀来流速度入口和自由出口边界条件，方柱展向采用周期性边界条件，方柱表面采用无滑移壁面边界条件。采用SIMPLEC格式求解压力速度耦合方程组，空间离散采用中心差分格式，时间离散采用二阶全隐式。

为了选取合适的湍流模型和计算参数，在风向角α=0°时，采用结构化网格比较了亚格子尺度模型、周向网格数量、量纲一化时间步、展向长度等参数对方柱气动性的影响，结果验证内容详见文献［14］。图3给出了α=0°时方柱表面风压系数（由方柱展向中间截面周向测点的风压时程曲线得到）与文献［15-18］结果的比较，可知本文计算的平均风压值和脉动风压值均与文献结果吻合良好，所以本文计算均采用大涡模拟湍流模型和WALE亚格子尺度模型。图4为计算模型网格图，方柱的周向分布200个网格，在角部加密；近壁面最小网格厚度为0.001D；近壁面y＋≈1；展向网格长度为0.1D；计算模型的总网格数为59万；量纲一化时间步Δt*为0.025，其中Δt*= ΔtU0/D，Δt为时间步，U0为来流风速。

风压非高斯特性的统计参数定义如下：偏度（skewness）系数是风压三阶中心矩与均方差的三次方的比值，记为S，如式（1）所示；峰度（kurtosis）系数为风压四阶中心矩与均方差的四次方的比值，记为K，如式（2）所示：

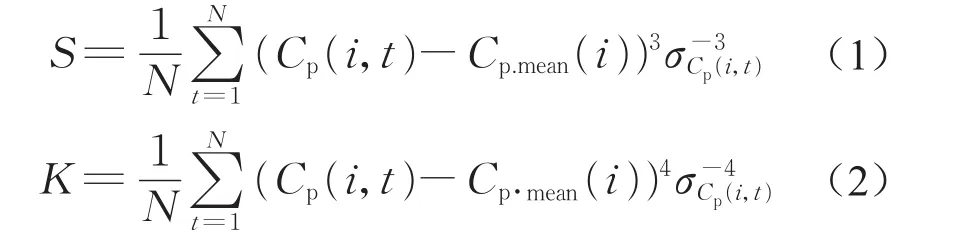
式中：N为风压系数时程的样本数；Cp(i，t)为方柱表面第i个测点的压力系数时程；Cp.mean(i)为方柱表面第i个测点的平均压力系数；σCp(i，t)为方柱表面第i个测点压力系数时程Cp(i，t)的均方差。

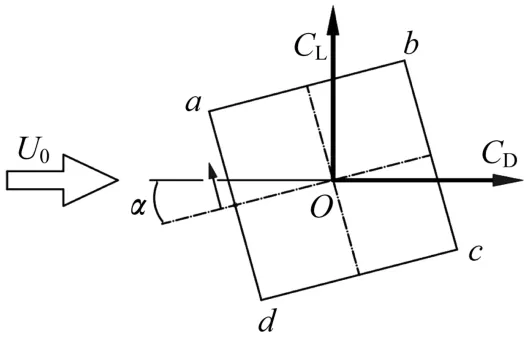
图1 计算模型示意图Fig.1 Sketch of computational model

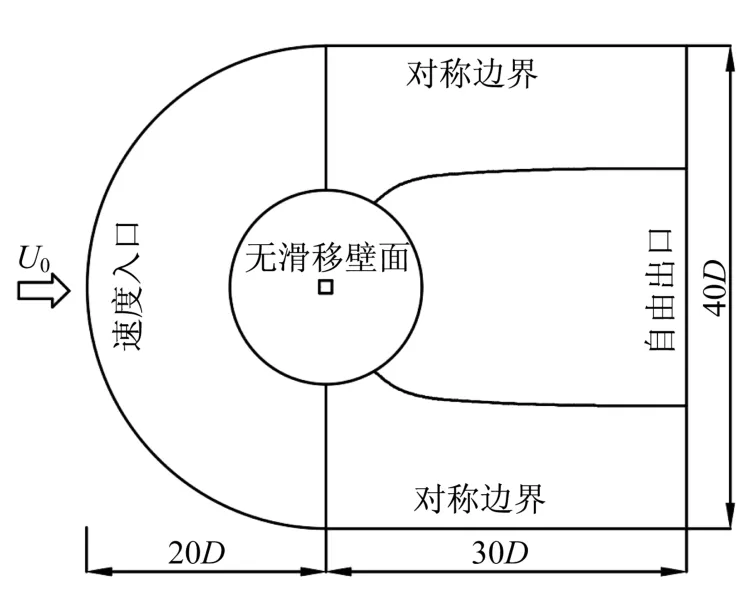
图2 计算域及边界条件Fig.2 Computational domain and boundary condition

图3 α=0°时的方柱表面风压系数Fig.3 Pressure coefficient distribution of square cylinder for α=0°

图4 计算模型的网格Fig.4 Computation grid scheme

2 计算结果及分析

2.1 表面风压系数

图5为方柱表面平均风压和脉动风压系数随风向角的变化曲线，图中Cp.mean为方柱表面平均风压系数、Cp.rsm为方柱表面脉动风压系数。

由图5a可知，不同风向角的平均风压系数差异很大，特别是在风向角α=12.5°和20.0°（分离泡流态）时，方柱上侧面（ab）的负压会出现明显的波动。然而方柱背风面（bc）和下侧面（cd）的负压均随风向角（除α=0°）的增大而增强，这与方柱上侧面（ab）的变化趋势相反。

由图5b可知，方柱下侧面（cd）的脉动风压随风向角（除α=0°）的增大而增大，与方柱上侧面（ab）的变化趋势相反。特别是在α=0°（前角分离流态）时，方柱上、下侧面的脉动风压明显大于其他工况值，并在方柱各角部位出现明显“跳跃”现象。同时在α=12.5°和20.0°（分离泡流态）时，方柱上侧面（ab）的脉动风压出现明显的变化。当α=45.0°（附着流流态）时，方柱下侧后角c点的脉动风压达到峰值，与平均风压的变化趋势相似。

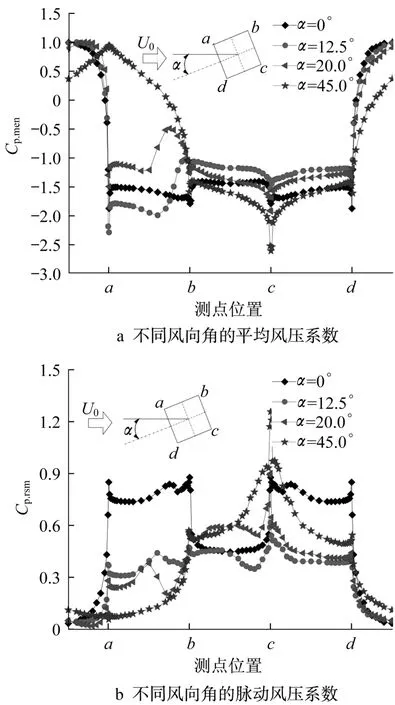
图5 方柱表面风压系数分布随风向角的变化Fig.5 Pressure distribution of square cylinder with angle of attack

2.2 风压的偏度和峰度

图6为方柱表面的风压偏度和峰度随风向角的变化曲线。图中S为方柱表面风压偏度系数、K为方柱表面风压峰度系数。从图6可知，方柱表面的风压偏度和峰度在相同风向角时沿方柱四周的变化规律相似，在不同风向角时均在方柱后角c点附近达到极值。

由图6a可得，绝大部分的风压偏度都是负偏，仅在部分风向角下才会出现正偏，而且方柱背风面（bc）和下侧面（cd）的风压偏度相对较大，特别是在方柱后角c点。当α=0°（前角分离流态）时，方柱绝大部分区域的风压偏度绝对值均大于0.2，而在α=12.5°和20.0°（分离泡流态）时，方柱上侧面（ab）分离泡区域的风压偏度很小。

由图6b可知，方柱上、下侧面靠近来流区域所有工况的风压峰度均较小，而方柱背风面（bc）的风压峰度较大。当α=0°（前角分离流态）时，仅方柱上、下侧面后角附近的风压峰度大于3.5。当α=12.5°和20.0°（分离泡流态）时，方柱上侧面（ab）分离泡区域的风压峰度明显比下侧面（cd）的风压峰度小。在α=45.0°（附着流流态）时，方柱下侧后角c点的风压峰度存在突变。

图6 方柱表面风压非高斯特性随风向角的变化Fig.6 Non-Gaussian feature of pressure on square cylinder with wind angle

2.3 风压非高斯区域与平均流场

图7为风压非高斯区域与平均流场图。图中X为顺风向坐标、Y为横风向坐标、Cp为平均流场风压系数，其中X/D为顺风向坐标比、Y/D为横风向坐标比。参照楼文娟等［7］的标准作为风压非高斯区域的判定依据：即偏度|S|＞0.2且峰度|K|＞3.5。图7中黑色条形为风压出现非高斯特性的区域。文献［5］是研究C类风场下的方形高层建筑，根据其几何缩尺比及模型尺寸，选取模型离地面2/3高度截面的试验数据与本文结果进行对比分析，得出大涡模拟的风压非高斯区域与文献［5］结果基本一致。风压非高斯区域主要出现在方柱后角部位和背风面（bc），而在方柱上侧面（ab）分离泡区域则没有出现明显的风压非高斯现象。方柱下侧面（cd）的风压非高斯区域随风向角的增大而逐渐变大，与方柱背风面（bc）的变化趋势相反。不同流态下的风压非高斯区域分布有所不同，但相同流态下的风压非高斯区域分布是相似的。由图7a～7d可得，方柱尾流回流区的范围随风向角的增大而逐渐变大。特别是α=12.5°和20.0°（分离泡流态）时，方柱上侧面（ab）剪切层再附形成的分离泡，并未引起明显的风压非高斯现象。当α=0°（前角分离流态）时，方柱表面风压的非高斯区域仅出现在方柱后角部位。当α=45.0°（附着流流态）时，方柱后角c点附近存在对称的小漩涡。由图7e～7h可知，方柱整体的负压区域随风向角的增大呈现先减小后增大的趋势。同时发现负压较小区域和正压区域多为风压高斯区域，负压较大区域多为风压非高斯区域。然而在α=12.5°和20.0°（分离泡流态）时，方柱上侧面（ab）分离泡区域的负压虽比较大，但并未引起明显的风压非高斯现象。当α=45.0°（附着流流态）时，方柱后角c点处存在明显对称的风压非高斯区域。

2.4 极值风压的流场机理

随机出现的极值风压是导致风压非高斯特性的主要原因，通过详细分析α=0°～45.0°具有风压非高斯特性测点的瞬态流场结构，得到如图8所示的极值风压流场机理示意图。根据极值风压产生的原因可将其流场作用机理分为两类，一种是角部附着涡作用机制，即方柱后角部的极值风压是由方柱角部部位间歇性出现的角部附着涡导致的；另一种是尾流卡门涡作用机制，即方柱背风面的极值风压是由尾流卡门涡的回旋作用引起的。限于篇幅，以风向角α=0°、12.5°、45.0°对这两类机制的瞬时和局部流场图做进一步分析。

图7 风压非高斯区域与平均流场的关系Fig 7 Relationship between non-Gaussian region and time-averaged field

2.4.1 角部附着涡作用机制

2.4.1.1α=0°流场机理

图9为测点A的风压时程和概率密度分布曲线。图中Cp（i，t）为方柱测点的风压系数时程。由图9a可知，测点A的风压时程曲线存在明显的向下偏移，且多处出现极值风压。由图9b可知，测点A的风压概率密度分布曲线明显向右倾斜形成较大的负偏，且曲线比较陡峭引起较大的峰度。图9a中给出了4个典型采样时刻。

图10为α=0°瞬时流线和局部流场（风压和流线）图，图中Cp为瞬时流场风压系数。从瞬时流线图可知，方柱上侧剪切层形成的分离涡（初始状态的尾流卡门涡）与纵穿方柱背风面的下侧流体在方柱后角部位相互作用，从而引起测点A的极值风压。从局部放大图中的风压系数可知，在T3时刻，测点A的风压最大，是缘于上侧剪切层分离涡在角部的分离作用，导致方柱表面出现逆时针间歇性的角部附着涡。虽在T4时刻，方柱表面也存在角部附着涡但并未引起极值风压，因为其是由剪切层回流区引起的顺时针附着涡。

图8 极值风压的流场机理Fig 8 Field mechanism of extreme pressure

2.4.1.2α=45.0°流场机理

图11为测点B的风压时程与概率密度分布曲线。从图11a可知，测点B的风压时程表现为明显的不对称，间歇性出现大幅值脉动风压。由图11b可知，在横坐标负值区，测点B的衰减速度比标准正态的变化较慢，形成明显的拖尾现象。为了进一步探究α=45.0°后角极值风压的形成机理，图11a中给出了4个典型采样时刻。

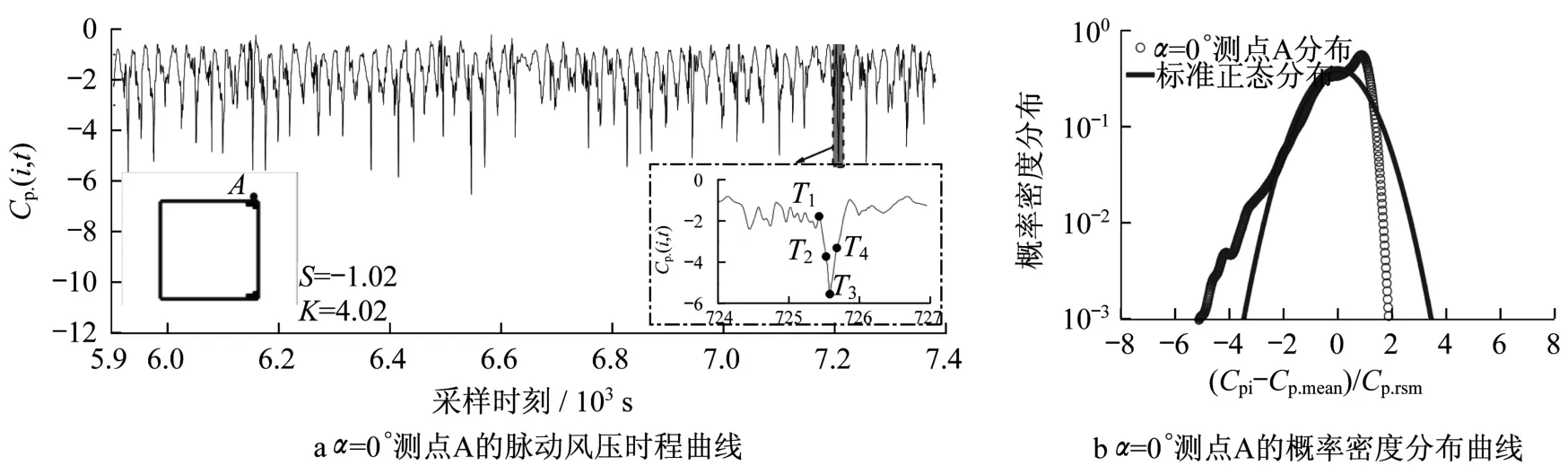
图9 α=0°测点A的脉动风压和非高斯特征Fig 9 RSM pressure and non-Gaussian feature of point A for α=0°

图10 α=0°瞬时流线与局部流场放大图Fig 10 Instantaneous streamline and local amplification field for α=0°

图11 α=45.0°测点B的脉动风压和非高斯特征Fig 11 RSM pressure and non-Gaussian feature of point B for α=45.0°

图12为α=45.0°瞬时流线和局部流场（风压和流线）图。从瞬时流线图可知，方柱上、下固定分离点附近存在恒在的分离涡，并不会引起明显的风压非高斯现象。当方柱尾流卡门涡在方柱后角作用时，会使测点B出现极值风压。从局部流场可知，在T3时刻出现极值风压，方柱表面出现间歇性的角部附着涡，同时测点B流体方向的改变也进一步促进了极值风压的出现。由此可知，方柱后角部位的极值风压是由间歇性出现的角部附着涡导致的，角部附着涡与方柱近尾流区的卡门涡有紧密的联系。

图12 α=45.0°瞬时流线与局部放大图Fig 12 Instantaneous streamline and local amplification field for α=45.0°

2.4.2 尾流卡门涡作用机制

图13为测点C的风压时程和概率密度分布曲线。由图13a可知，测点C的风压时程曲线整体向负轴向偏移，间歇性出现极值风压。由图13b可知，测点C的风压概率分布曲线有明显的非高斯特性，与风压时程曲线的特征相吻合。为了进一步探究方柱背风面极值风压的形成机理，图13a中给出了4个典型采样时刻。

图14为α=12.5°瞬时流线和局部流场（风压和流线）图。从图14可知，当方柱上侧尾流卡门涡向下移动的过程中最靠近方柱背风面时，测点C出现极值风压，同时方柱下侧流体受尾流卡门涡的挤压作用也进一步促进该点极值风压的产生。从局部放大图可知，在T3时刻测点C出现极值风压时，此时并没有明显的间歇性附着涡，而是由贴近测点C的尾流卡门涡的回旋作用引起的，出现极值风压的位置也会随尾流卡门涡的移动而改变。

图15为分离泡测点的风压时程和概率密度分布曲线。由图15a可知，分离泡测点的风压时程相对稳定。由图15b可知，分离泡测点的风压概率密度分布曲线与标准正态的变化吻合良好，也再次证明分离泡区域的风压表现出明显的高斯特性。

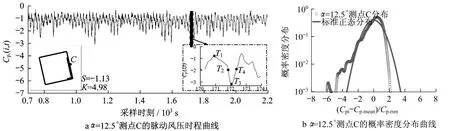
图13 α=12.5°测点C的脉动风压和非高斯特征Fig 13 RSM pressure and non-Gaussian feature of point C for α=12.5°

3 结论

对雷诺数为22 000的方柱进行大涡模拟，研究了均匀流作用下方柱表面风压非高斯特性随风向角的变化规律，分析了风压非高斯区域与平均流场的关系，并从流场角度阐述了方柱表面极值风压和风压非高斯特性的形成机理。主要结论如下：

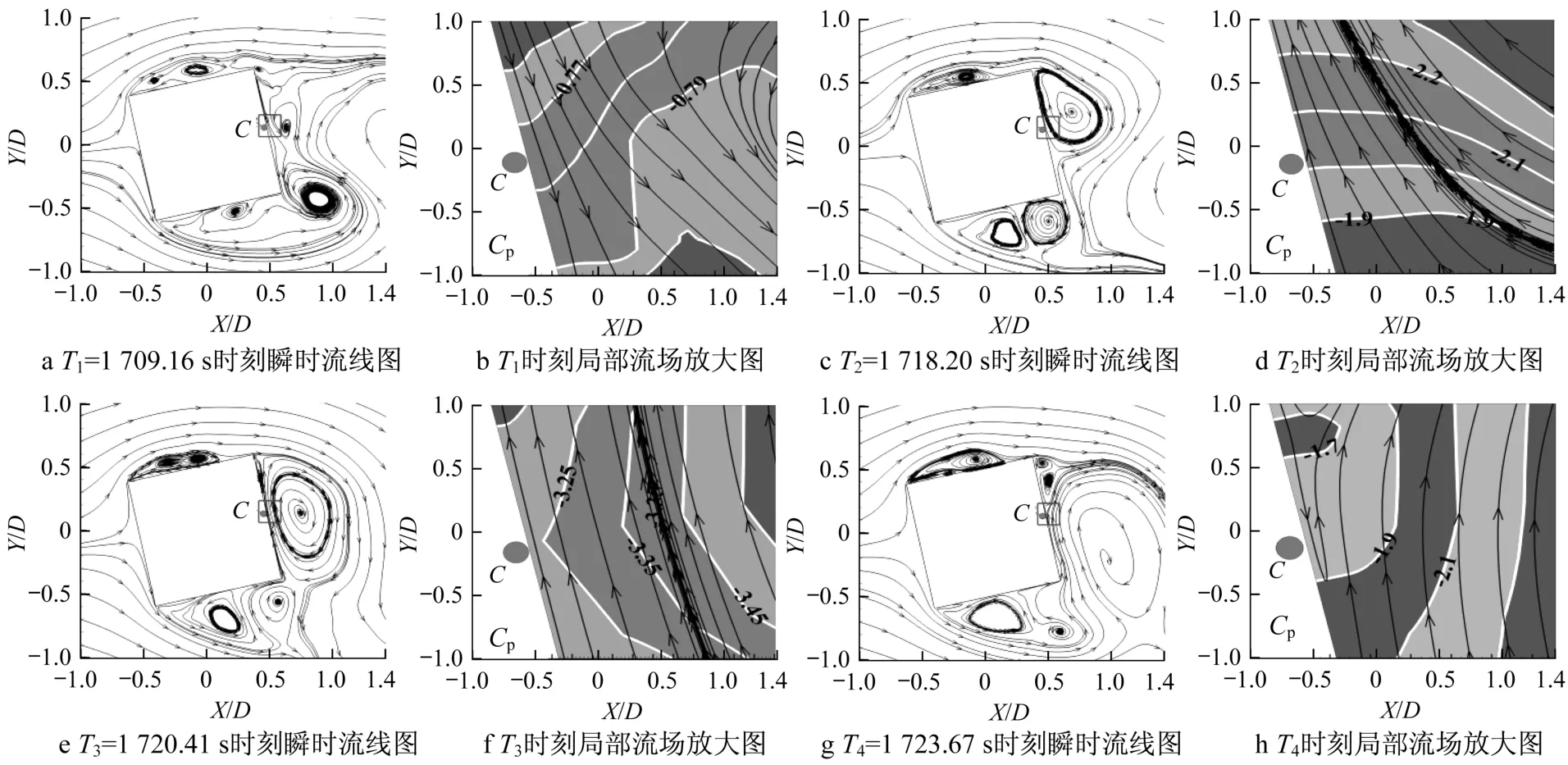
图14 α=12.5°瞬时流线与局部放大图Fig 14 Instantaneous streamline and local amplification field for α=12.5°

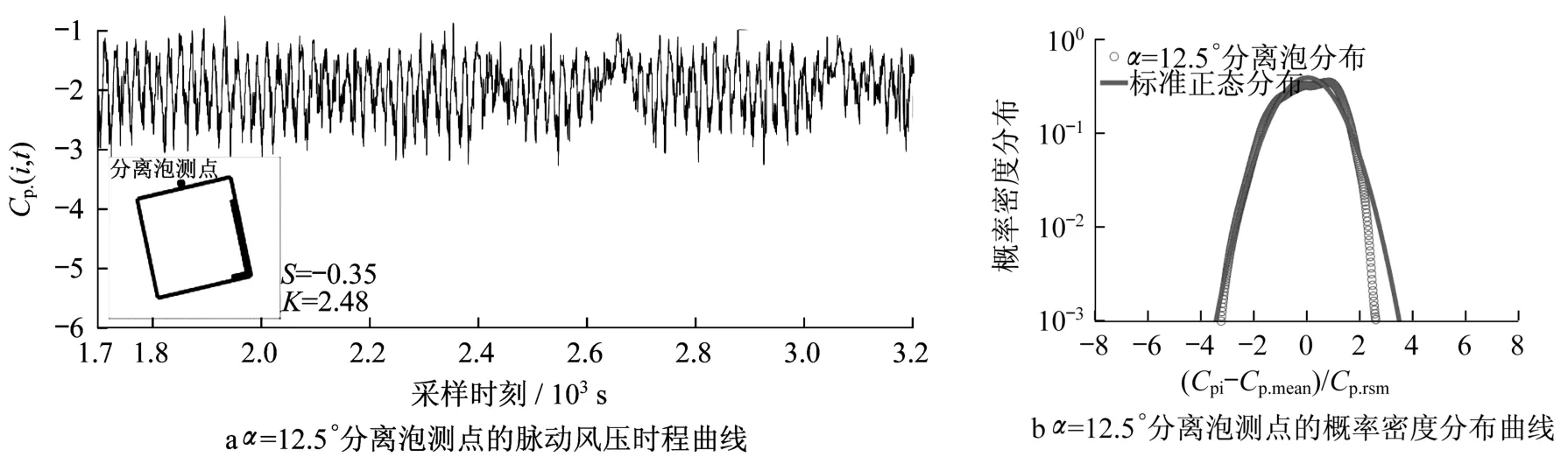
图15 α=12.5°分离泡测点的脉动风压和非高斯特征Fig 15 RSM pressure and non-Gaussian feature of measuring point separation bubble for α=12.5°

（1）方柱表面的风压偏度和峰度在相同风向角时沿方柱四周的变化规律相似，在不同风向角时均在方柱后角部位附近达到极值。

（2）方柱表面的风压非高斯区域主要为方柱后角部位和背风面，而剪切层再附形成的分离泡区域则不会出现明显的风压非高斯现象。风压非高斯区域与方柱的流场结构有密切关联。方柱下侧面的风压非高斯区域随风向角的增大而逐渐变大，与方柱背风面的变化趋势相反。

（3）方柱后角部位的极值风压是由间歇性出现的角部附着涡导致的，角部附着涡则与方柱近尾流区的卡门涡有紧密的联系；而方柱背风面的极值风压则是由方柱尾流卡门涡的回旋作用引起的，出现极值风压的位置会随尾流卡门涡的移动而改变。

需要指出的是，实际超高层建筑的风压非高斯特性受多种因素的影响，如：大气边界层风特性、截面形状、高宽比和端部效应等。而本文为了简化研究问题，避免多因素的叠加效应，仅研究了均匀来流下的方柱极值风压和风压非高斯特性的流场机理。为了进一步澄清风压非高斯特性的机理，有必要进一步研究平均风剖面、来流湍流度、截面形状等因素对风压非高斯特性的影响规律。