均匀流中矩形高层建筑脉动风压的阻塞效应试验研究

黄 剑，顾 明

(同济大学 土木工程防灾国家重点实验室，上海 200092)

风洞试验是进行结构风工程研究最为重要的手段之一。风洞通常是封闭的管道，以洞壁为边界，用有限的空间来模拟真实大气的无限空间必然伴随着洞壁干扰，即阻塞效应。

在进行风洞试验时，通常认为将模型阻塞度控制在5%以下所引起的阻塞效应可以忽略不计[1]。但目前很少有文献涉及阻塞效应对建筑结构风洞试验结果的影响。Raju等[2-6]研究了二维方柱平均阻力系数的阻塞效应，采用在相同风洞中变化模型缩尺比进行试验研究，分别提出了平均阻力系数的修正公式；谢壮宁等[7-8]初步探讨了阻塞效应所引起的模型表面平均和根方差风压的幅值特性，但还应对建筑表面脉动风压的相关性和相关性等特性研究。对脉动风压的深入探讨将揭示阻塞效应的一些机理，但目前这方面的研究甚少。

本文分别对阻塞度为4.1%、6.1%、8.4%和10.1%的CAARC标准高层建筑刚性模型在均匀风场中进行测压试验，考察了模型表面测点根方差脉动风压系数、风压系数功率谱、空间相关性和相干性。均匀风场中作用在建筑上的脉动风压主要源于气流在建筑物上的分离和旋涡脱落等复杂的空气动力流动，而和来流紊流无关。本文的目的是研究单体矩形高层建筑在这一流动条件下的脉动风压阻塞效应的规律。

1 风洞试验概况

本试验在同济大学土木工程防灾国家重点实验室TJ-2大气边界层风洞中完成。试验采用均匀风场，对于矩形柱这样的带有尖角的钝体，分离点固定在迎风前缘的角部位置，可认为不受雷诺数效应的影响。控制来流风速为14m/s，湍流度约为1%。由于风洞边界层的影响，0.3 m以下的区域内平均风速和湍流度的均匀性不如上部。

风洞试验模型尺寸见表1。图1-图2表示各层测点的布置和编号。例如，测点13-8代表模型第13层的8号测点。试验模型用5 mm厚有机玻璃板制作，测压管长度均为1 000 mm。试验数据修正采用相同的管道修正函数[9]。 图3为风向角及模型基本坐标。本文仅在0°风向角(模型宽面迎风)下进行了研究。

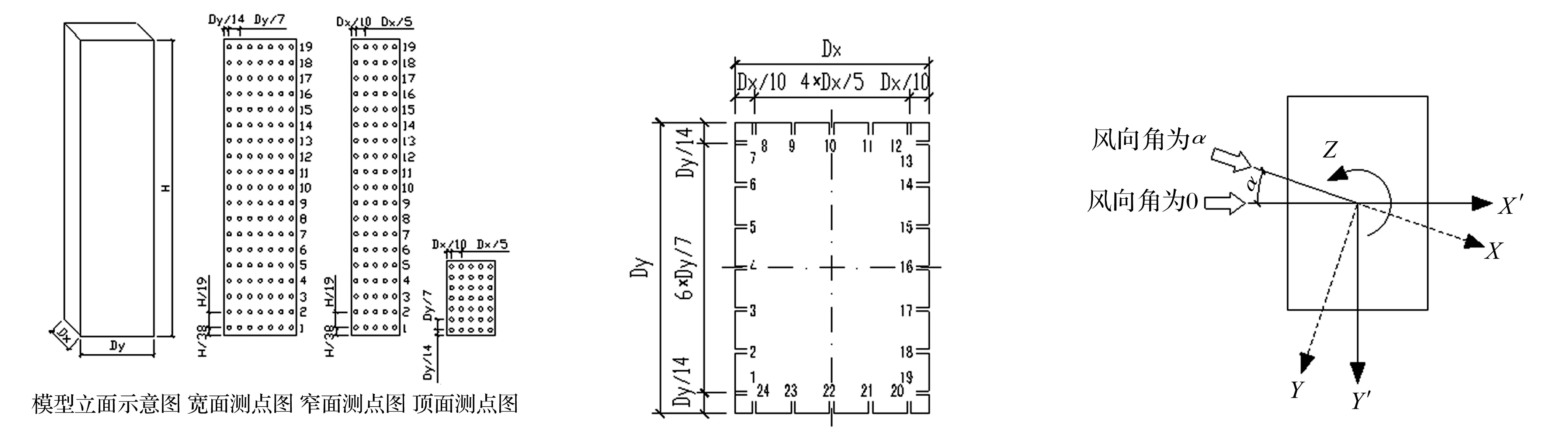
图1 模型立面及测点布置

2 典型测点的根方差脉动风压系数

将测点根方差脉动风压系数定义如下：

(1)

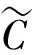
图4为典型测点的根方差脉动风压系数随阻塞度的变化情况。由图可见，除了在0.3 H以下受边界层影响外，迎风面对称轴处测点4的风压脉动主要与来流湍流有关，受阻塞度影响很小；迎风面边缘测点7的根方差脉动风压系数仍由来流湍流控制，但当阻塞度达到10.1%(为模型M4)时，模型中间层风压脉动的增大较为明显；随着阻塞度增大，侧面迎风前缘测点8在较低位置处的根方差脉动风压系数增幅较大；对于侧面后缘测点12和背风面边缘测点13，M4模型在0.2-0.3 H处根方差脉动风压系数的增大较为明显；背风面对称轴处测点16的根方差脉动风压系数增大。

总的来看，迎风面靠近对称轴处的脉动风压受阻塞度影响较小；在建筑表面易产生分离、涡脱处的脉动风压受阻塞效应的影响显著。M1和M2各面根方差脉动风压系数较为接近，认为在此情况下阻塞效应可以忽略。当阻塞度达到8.4%时，根方差脉动风压系数已有一定的增幅；当阻塞度达到10.1%时，在模型0.5 H以下的根方差脉动风压系数增大尤为显著，且改变了沿高度的分布规律。

3 风压系数的频谱特性

限于篇幅，仅考察13层(2/3 H处)各面对称轴测点的频谱特性。考虑实际结构的折减频率范围[10]，仅绘制折减频率0.01-1.0内的频谱。 图5为13层各面对称轴处的测点风压功率谱曲线。由图可见，对于测点13-4，随着阻塞度增大，折减频率为0.24(约为旋涡脱落频率的2倍)处将出现峰值；各模型测点13-10的风压功率谱均出现明显峰值；随着阻塞度增大，谱峰更为突出，且谱峰折减频率增大：M1为0.110，M2为0.113，M3为0.118，M4为0.121。阻塞度增大使旋涡脱落的能量和频率都增大；各模型测点13-16的功率谱曲线的频率成分都比较丰富，随着阻塞度增大，折减频率0.24处出现了明显峰值。研究表明[11-12]，旋涡脱落所诱发的结构顺风向脉动荷载主频是横风向脉动荷载主频的2倍。本文结果与此相同。

阻塞度增大使模型和洞壁之间的距离减小，引起模型位置处风洞横截面流速增大，导致模型侧面旋涡脱落的能量和主频都增大，从而模型侧面风压功率谱的峰值更突出，谱峰折减频率增大。另一方面，模型侧面剧烈的旋涡脱落诱发迎、背风面风压功率谱出现尖锐的峰值。

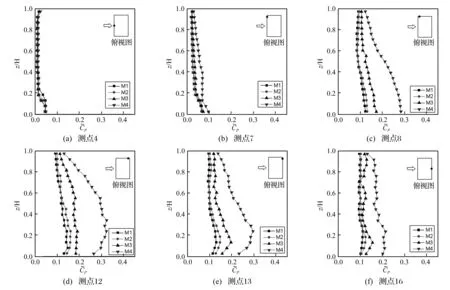
图4 典型测点根方差脉动风压系数随阻塞度的变化

图5 典型测点风压系数功率谱随阻塞度的变化

4 脉动风压的相关性

4.1 水平相关性

仅选取13层各面对称轴上的测点为基准点考察风压系数的水平相关性，将基准点风压与其他测点风压的相关系数绘于图6-图8中。

图6为测点13-4与迎、背风面风压相关系数。由图可知，测点13-4与背风面测点的风压相关性较低，均小于0.2。测点13-4与迎风面测点的风压相关性随距离增大而降低。随着阻塞度增大，测点13-4与迎风面相邻测点风压的相关性增强，但随距离增大的衰减更迅速。

图7为测点13-16与迎、背风面风压相关系数。由图可知，测点13-16与迎风面除角点以外的测点风压相关性较低，均小于0.3。测点13-16与背风面测点风压有较强的相关性，距离越大相关性越低。随着阻塞度增大，测点13-16与背风面其他测点的风压相关性减弱，且随距离增大的衰减更迅速。

图8为测点13-10与侧面其他测点风压相关系数。由图可知，测点13-10与同侧测点的风压相关性较强，均大于0.8，且受阻塞度影响很小。测点13-10与另一侧所有测点的风压相关性大致相同，并随阻塞度的增加显著降低，由正相关变为负相关。这表明，阻塞效应影响了两侧测点风压时程之间的同步性。

图6 测点13-4与迎、背风面风压相关系数

4.2 竖向相关性

选取各面对称轴上的点作为基准点分析风压时程的竖向相关性。 图9为各模型测点4的风压竖向相关系数。由图可见，M1和M2测点4的风压竖向相关系数分布规律相似，但M2图中的数值在距离对角线较远处稍大于M1。M3和M4测点4的风压竖向相关系数分布规律相似，随着阻塞度增大，迎风面测点风压的竖向相关性增大。M3图中相关系数大于0.4的区域占绝大部分，而M4图中相关系数大于0.5的区域占绝大部分。 图12为测点13-4与其它测点的风压相关系数。由图可见，迎风面测点风压的竖向相关系数随着距离增加而衰减，且阻塞度越大相关性越大。

图9 测点4风压竖向相关系数

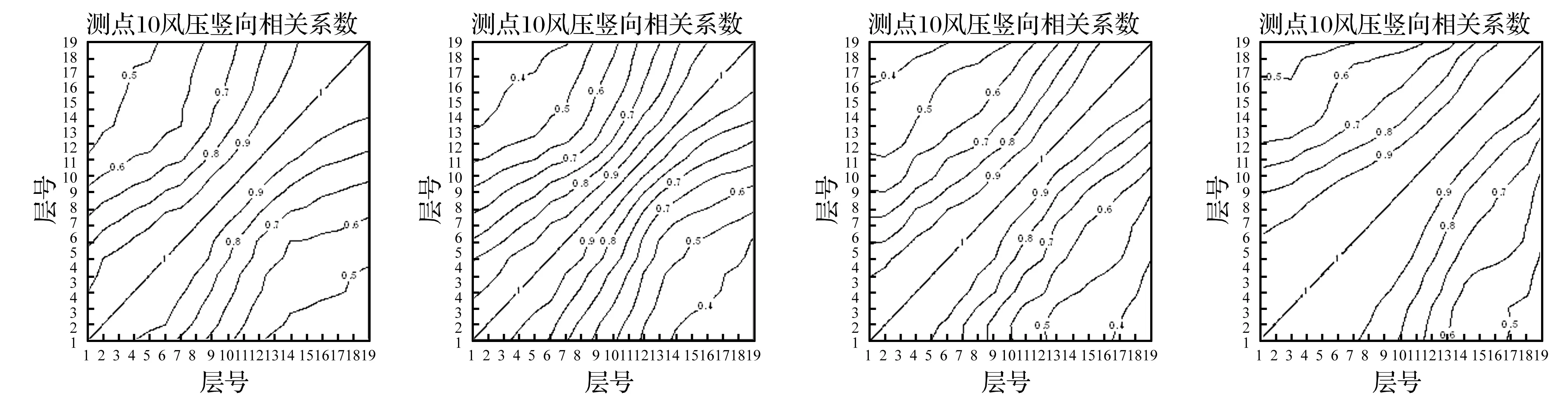
图10 测点10风压竖向相关系数

图10为各模型侧面测点10的风压竖向相关系数。由图可见，各模型测点10的风压竖向相关系数分布规律相似，随距离增大而降低。M1-M3测点10的风压竖向相关系数的分布规律和数值大小相似；M4测点10的风压竖向相关系数比上述3个模型稍大，且在0.5H以下的风压竖向相关性增大明显。 图13为测点13-10与其它测点的风压相关系数。由图可见，各模型侧面测点风压的竖向相关系数均随着距离的增加而平滑地衰减。阻塞度越大测点13-10与较低位置的风压相关系数越大，与较高位置的风压相关系数越低。

图11为各模型背风面测点16的风压竖向相关性。由图可见，M1和M2测点16的风压竖向相关系数的分布规律较为相似，但M2图中的数值在距离对角线较远处稍大于M1图中的数值。M3和M4测点16的风压竖向相关系数的分布规律与M1和M2的分布规律明显不同。随着阻塞度增大，背风面测点风压的竖向相关性减弱。图14为测点13-16与其它测点的风压相关系数。由图可见，各模型背风面测点风压的竖向相关系数随距离增大的衰减较为迅速。测点13-16与10层以下的测点风压的竖向相关系数较小，在0.3以内。随着阻塞度增大，测点13-16与13层以下测点的竖向相关性略有降低；测点13-16与15层以上测点风压的竖向相关性的降低较为显著。

图11 测点16风压竖向相关系数

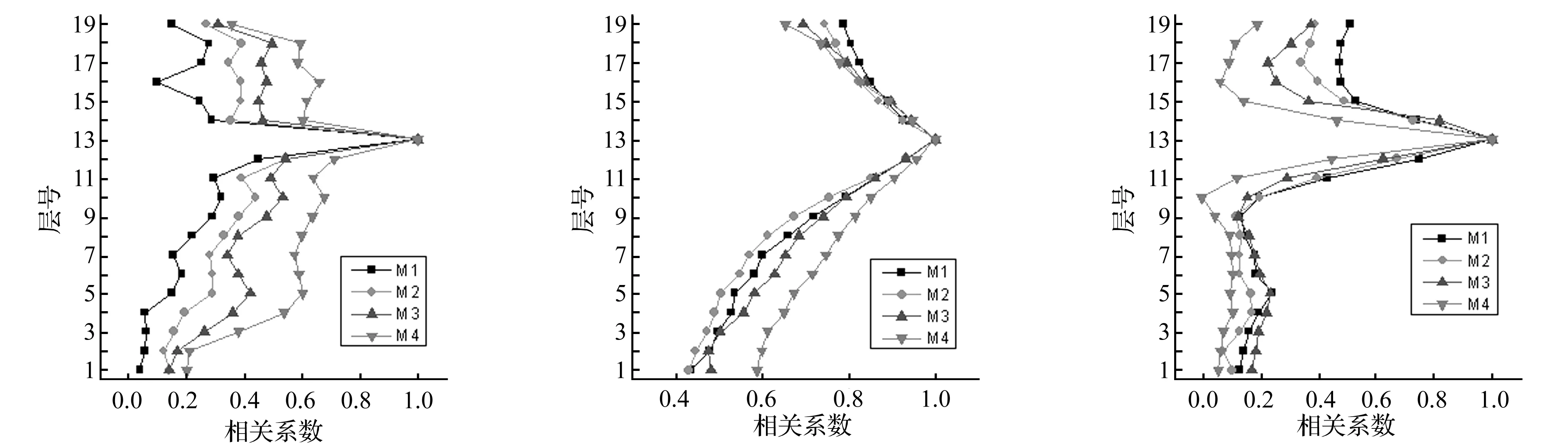
图12 测点13-4风压竖向相关系数

以上可见，在同一面上测点风压的水平相关性较强，不在同一面上测点风压的水平相关性较弱。随着阻塞度增大，迎风面相邻测点风压的水平和竖向相关性增大；背风面相邻测点风压的水平和竖向相关性降低；侧面同侧测点风压的竖向相关性增大，水平相关性几乎不受阻塞效应影响，但异侧测点的风压相关系数将会随阻塞度的增大由正值逐渐变为负值。对上述现象解释如下：阻塞效应使模型位置处的风洞横截面流速增大，且洞壁的存在影响了侧面绕流和尾流。流速的增大使迎风面测点空间相关性增强；在侧面靠近下部处，绕流受洞壁挤压严重，所以侧面同侧测点风压的竖向相关性增大；两侧旋涡脱落同步性的降低造成了异侧测点风压的水平相关性降低；当流体流经模型位置的截面后流速下降，且尾流受到洞壁的挤压，导致旋涡能量耗散，使背风面测点的空间相关性降低。

5 脉动风压的相干性

5.1 水平相干性

限于篇幅，仅研究13层各面对称轴上测点的水平相干性，并按照下式拟合[13]：

(2)

式中，Ch表示水平相干性系数；f为频率；d为两点水平距离；UH为模型高度处平均风速。

图15为各阻塞度模型迎风面、侧面和背风面测点风压水平相干函数。由图可见，侧面测点风压水平相干性的衰减比迎风面和背风面迅速。随着阻塞度增大，迎风面测点风压水平相干性逐渐增大；背风面测点风压水平相干性变化幅度较小；侧面测点风压水平相干性降低。对于迎风面、侧面和背风面而言，采用式(2)描述风压系数的水平相干性是比较合适的。从拟合得到的水平相干性系数Ch来看，迎风面在4-8之间，侧面在30-40之间，背风面在11-14之间。

图16为各阻塞度模型各面测点间的风压相干函数。由图可见，迎风面与背风面、迎风面与侧面、两侧面间测点风压相干性较弱。阻塞度的增大并没有显著影响这一特点。

5.2 竖向相干性

类似于风压的水平相干性，按照下式对竖向相干性函数拟合：

(3)

式中，Cz表示竖向相干性系数；其他符号同前。

图15 迎风面、侧面和背风面测点风压水平相干函数

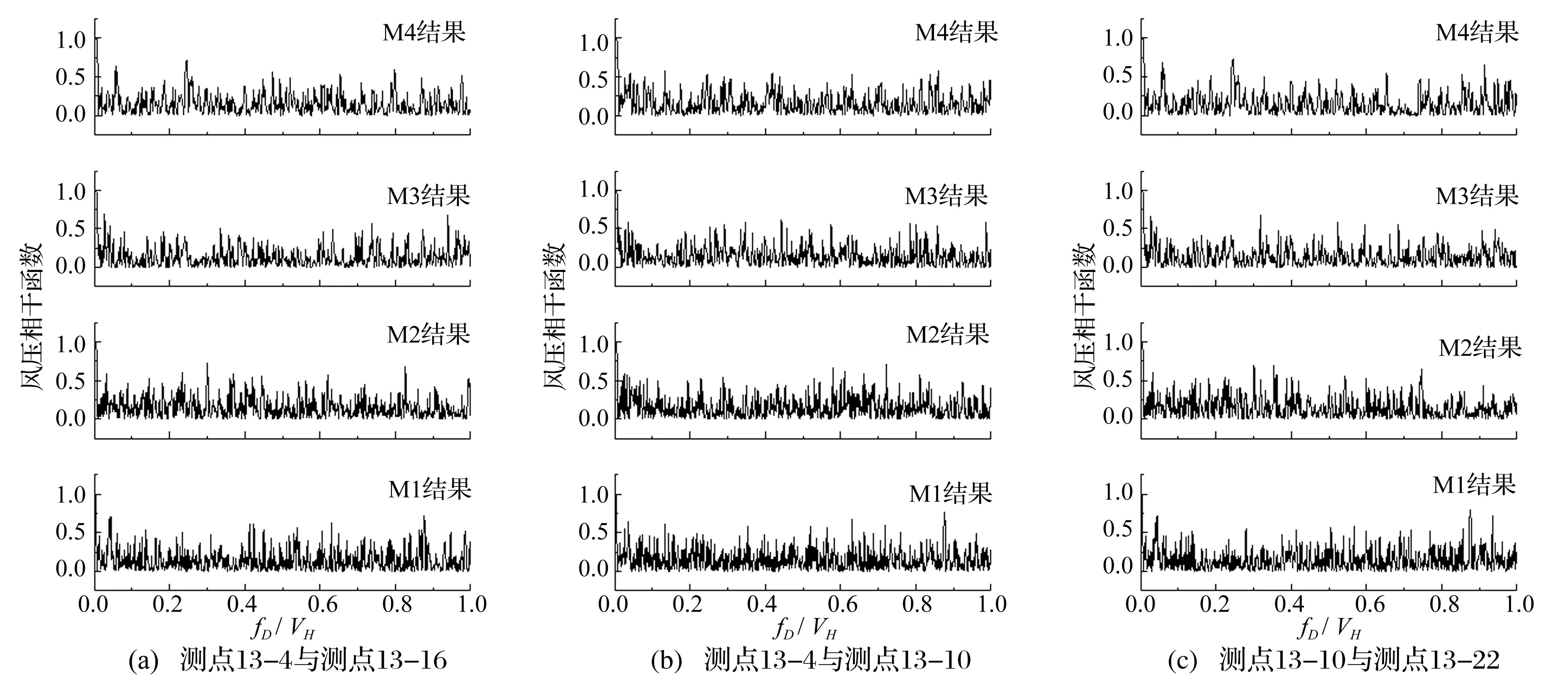
图16 各面测点间风压相干函数

图17为各阻塞度模型迎风面、侧面和背风面测点风压竖向相干函数。由图可见，随着阻塞度增大，迎风面和侧面测点风压竖向相干性逐渐降增大；背风面测点风压竖向相干性呈增大趋势。对于迎风面、侧面和背风面而言，采用式(3)描述风压系数的竖向相干性是比较合适的。从拟合得到的竖向相干性系数Cz来看，迎风面在4-8之间，侧面在9-13之间，背风面在12-24之间。

6 结 论

本文研究了均匀流场中矩形单体高层建筑阻塞效应对脉动风压的影响，得到如下结论：

(1) 建筑迎风面靠近对称轴处根方差脉动风压系数的阻塞效应较小；在易产生分离、涡脱处的根方差脉动风压系数受阻塞效应的影响显著；

(2) 阻塞度增大使模型侧面旋涡脱落的能量和主频增大，且侧面旋涡脱落的加剧导致了迎、背风面风压功率谱出现明显峰值；

(3) 随着阻塞度增大，迎风面相邻测点风压的空间相关性增大；背风面相邻测点风压的空间相关性降低；侧面同侧测点风压的竖向相关性增大，水平相关性几乎不受阻塞效应影响，但异侧测点的风压相关系数将由正值逐渐变为负值；

(4) 随着阻塞度增大，迎风面、侧面相邻测点风压的空间相干性增大；背风面相邻测点风压的空间相干性降低。

[1] Hunt A.Wind-tunnel measurements of surface pressures on cubic building models at several scales[J].Journal of Wind Engineering and Industrial Aerodynamics,1982，10(2): 137-163.

[2] Raju K G R，Singh V.Blockage effects on drag of sharp-edged bodies[J].Journal of Wind Engineering and Industrial Aerodynamics,1975，1: 301-309.

[3] Awbi H B.Wind-tunnel-wall constraint on two-dimensional rectangular-section prisms[J].Journal of Wind Engineering and Industrial Aerodynamics,1978，3(4): 285-306.

[4] Laneville A，Trepanier J Y.Blockage effects in smooth and turbulent flows: The case of two-dimensional rectangular cylinders[J].Journal of Wind Engineering and Industrial Aerodynamics，1986，22(2-3): 169-176.

[5] Laneville A.Turbulence and blockage effects on two dimensional rectangular cylinders[J].Journal of Wind Engineering and Industrial Aerodynamics,1990，33(1-2): 11-20.

[6] Noda M，Utsunomiya H，Nagao F.Basic study on blockage effects in turbulent boundary layer flows[J].Journal of Wind Engineering and Industrial Aerodynamics，1995，54-55(0): 645-656.

[7] 谢壮宁，刘帅，石碧青.低矮房屋标准模型的风洞试验研究[J].华南理工大学学报(自然科学版)，2011，39(6): 106-112.

XIE Zhuang-ning，LIU Shuai，SHI Bi-qing.Investigation into wind tunnel test of standard low-rise building model [J].Journal of South China University of Technology (Natural Science Edition),2011，39(6):106-112.

[8] Wang L，Liang S G，Tang H Q，et al.Investigation on wind tunnel blockage effect of super high-rise building[C].Shanghai,China: 2012.

[9] 周晅毅，顾明.单通道测压管路系统的优化设计[J].同济大学学报(自然科学版),2003，31(7): 798-802.

ZHOU Xuan-yi，GU Ming.Optimization of dynamic pressure measurement of single-channel tubing systems [J].Journal of Tongji University (Natural Science),2003，31(7): 798-802.

[10] 徐安，谢壮宁，葛建斌，等.CAARC高层建筑标准模型层风荷载谱数学模型研究[J].建筑结构学报,2004，25(4): 118-123.

XU An，XIE Zhuang-ning，GE Jian-bin，et al.Mathematical model research of power spectrum of wind loads on CAARC standard tall building model [J].Journal of Building Structures,2004，25(4): 118-123.

[11] 顾明，项海帆.几种矩形二维柱体节段模型上脉动力的测量[J].空气动力学学报,1994,12(1): 115-119.

GU Ming，XIANG Hai-fan.Measurements of fluctuating force on 2-dimensional models of rectangular cylinders[J].Acta Aerodynamica Sinica,1994，12(1):115-119.

[12] 顾明，叶丰.典型超高层建筑风荷载频域特性研究[J].建筑结构学报,2006，27(1):30-36.

GU Ming，YE Feng.Frequence domain characteristics of wind loads on typical super-tall buildings [J].Journal of Building Structures,2006，27(1):30-36.

[13] 叶丰，顾明.超高层建筑风压的频域特性[J].同济大学学报(自然科学版),2006，34(3):285-290.

YE Feng，GU Ming.Frequency characteristics of wind pressure on super-tall buildings [J].Journal of Tongji University (Natural Science)，2006，34(3):285-290.