锥齿行星齿轮传动相位调谐研究*

谢　帮， 王世宇，2，3

(1.天津大学机械工程学院， 天津 300072；2.天津大学机构理论与装备设计教育部重点实验室， 天津 300072；3.天津市非线性动力学与混沌控制重点实验室，天津 300072)



锥齿行星齿轮传动相位调谐研究*

谢帮1， 王世宇1，2，3

(1.天津大学机械工程学院， 天津 300072；2.天津大学机构理论与装备设计教育部重点实验室， 天津 300072；3.天津市非线性动力学与混沌控制重点实验室，天津 300072)

根据锥齿行星齿轮传动的结构和受力的对称性，采用解析方法研究了啮合相位对振动特性的影响，揭示了中心轮齿数和行星轮个数与中心构件的受力及振动特性之间的关系，归纳出3种典型振动模式：轴向平移-扭转、径向平移-扭摆和受力平衡模式。在轴向平移-扭转振动模式下，中心构件呈现轴向平移和绕该轴的扭转振动；在径向平移-扭摆振动模式下，中心构件呈现沿径向的平移和绕该方向的扭摆振动；在受力平衡模式下，中心构件均不振动。数值计算及文献对比证明了解析预测的正确性及其在减振方面的有效性。

锥齿行星齿轮传动; 时变啮合刚度; 相位调谐; 振动模式

引　言

锥齿行星齿轮传动是一种常见的传动装置。中心轮的齿数和行星轮的个数是影响传动性能的重要基本参数。本文拟根据几何构型和啮合力的对称性，研究参数与受力及振动响应之间的调谐关系。

早在1967年，Schlegle和Mard就揭示了调谐现象[1]，Seager给出了初步解释[2]。Kahraman研究了斜齿行星传动相位调谐，揭示了振动模式及其抑制规律[3-5]。Parker等采用严密的数学推导和仿真计算，研究了直齿行星传动的相位调谐[6-11]。秦大同、肖正明等[12-13]和段福海等[20]也研究了与啮合相位有关的问题，得到了许多具有理论和工程意义的结论。本文作者提出了基于相位调谐的基本参数选择方法[15]。

应当指出的是，上述文献通常采用刚体假设，还有文献研究了弹性振动规律[11,16-18]。事实上，相位调谐源于结构及受力的对称性，与所采用的假设没有必然关系。为了避免应用无延展约束条件，同时提高分析效率，本文作者计入了弯曲和延展变形，采用叠加方法分析了齿圈的面内振动特性，揭示了齿数和行星轮个数与刚柔耦合振动之间的相位调谐关系[19]，之后将其推广至一般旋转对称式驱动/传动系统[20-22]。

锥齿行星传动几何构型对称且含脉动激励，因此应当存在相位调谐现象。文献[23]研究了该传动的齿数和行星轮个数与轴向力之间的关系，并设计了3种典型传动方案，分别研究了轴向力的变化规律，还给出了验证。由于仅讨论了含特定数目行星轮的情形，还需开展理论研究，分析其他参数选取方案对受力及振动的影响，揭示一般规律。

文献[24]采用相对质心的动量矩定理建立了锥齿行星传动的动力学模型，揭示了几种典型自由振动模式。基于该模型，本文进一步研究受迫振动特性，揭示参数与典型振动之间的映射关系，还将以时变啮合刚度为主要激励给出仿真验证。文献对比进一步证明了解析结论及其减振效果。

1　动力学模型

图1为文献[24]建立的锥齿行星传动计算模型。3个中心构件有3个平动和3个扭转运动，共计6个自由度；行星轮有3个平动和1个扭转运动，共计4个自由度。为了方便分析，建立了系杆随动坐标系，其中坐标轴xi(i=c,s1,s2)指向1号行星轮的平衡位置，z轴均沿旋转轴指向外侧。各行星轮坐标系的原点均位于质心平衡位置，xj(j=1,2,3,…,N;N为行星轮个数)沿系杆径向向外，yj由右手定则确定。各中心构件的坐标为(xi,yi,zi,uix,uiy,uiz)，第j个行星轮的坐标为(xj,yj,zj,ujx)。根据牛顿第二定律可得运动方程

(1)

式中M，ωc，G，Kb，Km，KΩ和F分别为质量矩阵、系杆角速度、陀螺矩阵、支承刚度矩阵、啮合刚度矩阵、向心刚度矩阵和激励向量，广义坐标q=[xc,yc,zc,ucx,ucy,ucz,xs1,ys1,zs1,us1x,us1y,us1z,xs2,ys2,zs2,us2x,us2y,us2z,x1,y1,z1,u1x,x2,y2,z2,u2x,…,xN,yN,zN,uNx]T。应当指出的是，本文仅针对相位调谐问题开展研究，忽略了间隙等非线性因素的影响。

图1　锥齿行星齿轮传动数学模型Fig.1　Mathematical model of bevel planetary gear trains

2　相位调谐研究

2.1受力分析

本文以中心轮1为例进行受力分析。假定齿数为Zs1，其与第j个行星轮之间的啮合力为Fj。如果啮合力沿中心轮的径向、切向和轴向的投影分别为Fj1，Fj2和Fj3，则啮合力沿3个坐标方向的投影为

(2)

式中ψj为第j个行星轮与横轴的夹角，且有

(3)

上述啮合力Fj为啮合误差及啮合刚度等啮频激振力。将式(2)中的Fj1，Fj2及Fj3分解为以啮频ωm为基频的傅立叶级数

(4)

式中l为谐波阶次，φj为第j个啮合位置的时间相位。文献[6]给出了直齿行星传动的啮合相位，根据两种传动的结构及受力的相似性，有

(5)

所有行星轮作用于太阳轮1的合力沿3个坐标方向的投影为

(6)

同理，作用于太阳轮1的合力矩为

(7)

式中rs1为等效集中啮合力与中心轮1的旋转中心的距离。对于整数m和M有[6]：

(8)

根据三角函数的运算特性，由式(2)～(9)可得中心轮齿数及行星轮个数等基本参数与振动响应之间的映射关系：

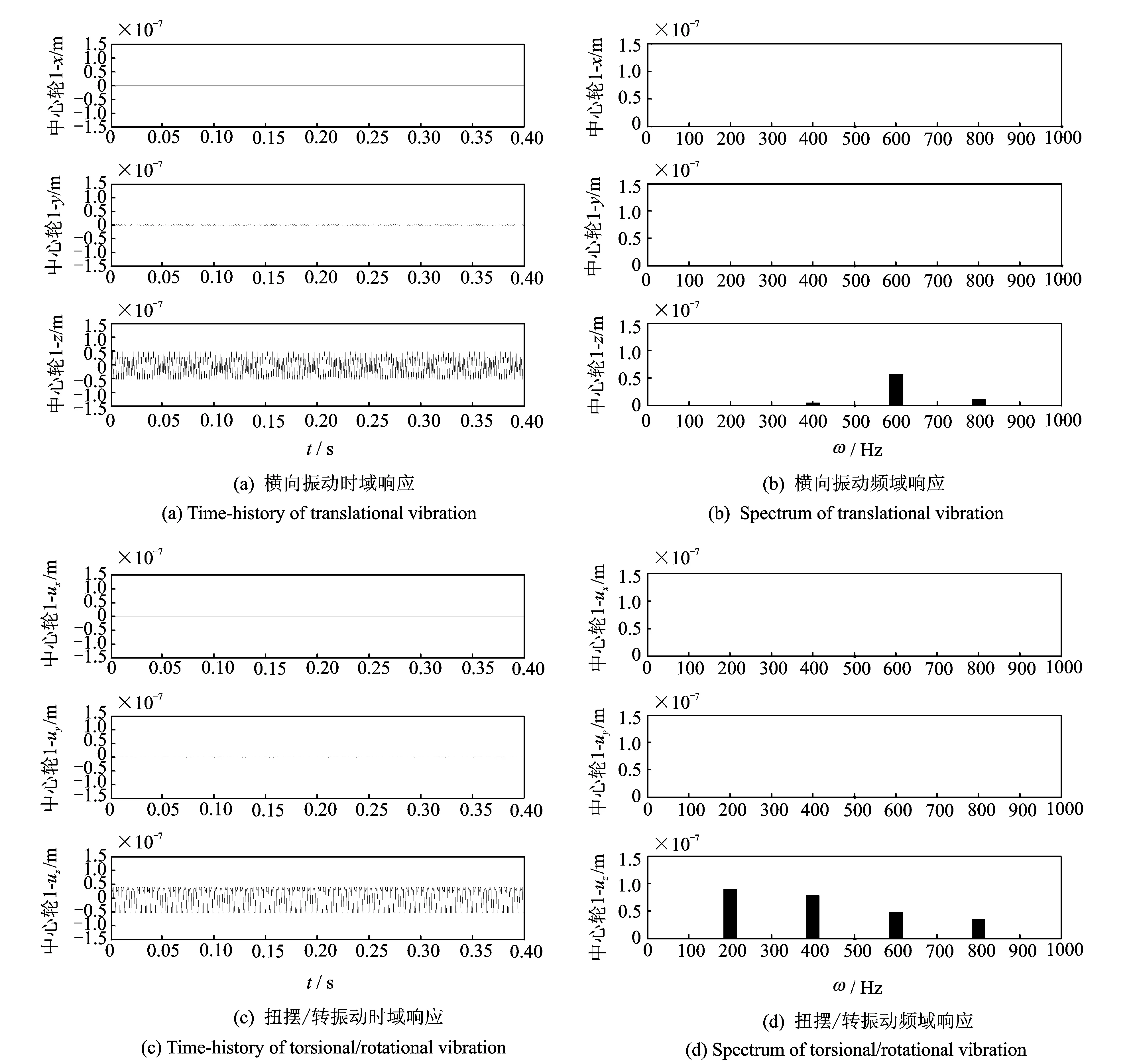
在上述结论中，q为整数，c满足1

2.2参数奇偶性分析

文献[19]揭示了中心轮齿数和行星轮个数等基本参数的奇偶性对直齿行星传动振动特性的影响规律。对于锥齿行星传动，上述参数也可以为偶数或奇数。奇偶性将影响啮合相位，进而改变构件的受力及振动特性。假定整数C为两个基本参数的最大公因子，根据文献[19]，当该因子大于1时，必然有lZs1≠qN±1，因此不存在RTT模式。同时，受装配条件2Zs1/N=整数的约束，对于双行星轮传动系统，中心轮齿数与行星轮个数可满足互质关系(C=1)，因此将激起3种振动模式；若行星轮个数为大于2的偶数，则必然有C>1，因此不存在RTT模式；若行星轮个数为奇数，则中心轮齿数可以被行星轮个数整除(C=N)，因此仅能激起ATR模式。综上可得表1所述相位调谐规律。

表1　锥齿行星传动相位调谐

3　结果验证

为了验证相位调谐规律，本文设计了3个传动方案，并根据表1预测了振动响应，如表2和3所述。对于方案A，由于中心轮齿数为奇数，因此随着啮频谐波阶次的改变，将分别激起ATR和RTT模式；对于方案B，两个参数满足整除关系，因此对于任意谐波阶数，仅能激起ATR模式；方案C两参数的公因子大于1，因此不存在RTT模式。

本文计入啮合刚度的时变性，并假定其按矩形波规律变化，极值分别为8.15×108和4.17×108N/m，重合度、输入扭矩和啮频分别为1.40，200 N·m和100 Hz。图2给出了啮合刚度波形及频谱。

图2　啮合刚度及其谐波Fig.2　Waveform and spectrum of mesh stiffness

应用傅立叶级数方法[25]求解式(1)，可得3个传动方案的时域和频域解。需要指出的是，因中心构件振动规律相似，本文仅给出中心轮1的振动响应，如图3～5所示。其中，图3为方案A的时频振动响应。由于中心轮齿数不能被行星轮个数整除，因此随着啮频谐波阶次的改变，可激起ATR和RTT模式。由图3(a)和(b)可知，奇数阶啮频谐波激起径向振动，但没有激起轴向振动，与表1和3所述解析预测一致。同时，根据表1，还应出现绕两个正交方向的扭摆振动，但从图3(c)和(d)可知，仅有绕y向的振动。原因在于方案A只有两个行星轮，且在仿真计算中假定轴心均位于x轴，啮合力投影为零，因此没有出现绕该轴的扭摆振动，但仍然可归结为RTT模式。相比之下，在偶数阶谐波处，中心轮呈现沿旋转轴的平移振动和绕该轴的扭转振动，表现为典型的ATR模式。上述计算结果与理论预测一致。

表2　锥齿行星传动基本参数

表3　传动方案及其振动模式

图3　时频振动响应(方案A)Fig.3　Time-frequency vibration (Case A)

图4　时频振动响应(方案B)Fig.4　Time-frequency vibration (Case B)

图4为方案B的中心轮1的时频振动响应。由于中心轮齿数可被行星轮个数整除，不论谐波阶次取何值，始终有lZs1≠qN±1，因此激起ATR模式。由图4可知，中心轮1的径向平移和扭摆振动均被抑制，但沿旋转轴的平移振动和绕该轴的扭转振动十分明显。上述结果与理论预测一致。

图5为方案C的中心轮1的时频振动响应。由于该方案的中心轮齿数与行星轮个数的公因子大于1，因此不存在RTT模式。由图5可知，不论谐波阶次取何值，均不存在关于x和y轴的平移和扭摆振动。在啮频的第4、第6和第8阶谐波处，满足lZs1=qN，表现出ATR振动模式。在第1、第3、第7和第9阶谐波处，中心轮的振动受到抑制，表现为FB模式。上述结果与理论预测一致。

根据本文揭示的相位调谐规律可进一步分析文献[23]的4个传动方案的振动特性。表4给出了各方案的中心轮齿数和行星轮个数。文献[23]指出：以轴向振动为评价标准，方案Ⅳ最好。根据本文结论，方案Ⅰ和Ⅱ始终满足lZs1=qN，因而激起ATR振动模式，产生显著的轴向振动。而方案Ⅲ和Ⅳ满足其他条件，可激起RTT和FB模式。由于不存在轴向振动，因此这两个方案较好。方案Ⅲ与Ⅳ的差别仅在于行星轮齿数的奇偶性。事实上，如果齿数为奇数，则内、外啮合相位相反，轴向啮合力不能抵消；如果为偶数，则上述两处啮合同相[4]。若不计制造和安装误差，偶数齿行星轮可使轴向啮合力抵消，因而抑制轴向振动。综上可知，方案Ⅳ的轴向振动小于其他方案。上述分析，一方面证明了文献[23]的结论，另一方面也证明了相位调谐规律的正确性及其在减振方面的有效性。

表4　锥齿行星传动方案[23]

图5　时频振动响应(方案C)Fig.5　Time-frequency vibration (Case C)

应当指出的是，本文仅分析了稳态响应。如果啮频或其谐波与某阶固有频率接近，同时啮合力的施加方式与自由振动模式一致，将激起共振。作为典型的参激系统，锥齿行星传动存在稳定性问题[26]和边频结构[27]。但是，在应用傅立叶级数解法时由于忽略了时变刚度与响应形成的二阶小量，将参激振动简化为受迫振动，因此所得结论仅描述了主频及其谐波响应。

鉴于锥齿行星传动的结构对称性及典型的参数激励特征，有必要分析由啮合刚度激励产生的边频叠加效果，以充分揭示相位调谐规律。Parker等深入研究了齿圈系统的参激振动规律，得到了许多有意义的结论[28]。为了避免烦琐的动力学建模和解析分析，可考虑采用弹性波叠加方法[19]分析各啮合位置的振动叠加效果，最终揭示计入延展变形的参激振动规律。

4　结　论

本文研究了锥齿行星齿轮传动的基本参数对振动特性的影响。根据中心构件的振动特征，本文揭示了3类典型振动模式，即：轴向平移-扭转、径向平移-扭摆和平衡模式。在第1种模式下，中心构件仅存在轴向平移和绕该方向的扭转振动；在第2种模式下，中心构件仅存在径向平移和扭摆振动；在平衡模式下，中心构件6个方向的振动均被抑制，因此处于受力平衡状态。仿真计算及文献对比证明了解析结果的正确性及其在减振方面的有效性。

[1]Schlegel R G,Mard K C. Transmission noise control approaches in helicopter design [C]. ASME 67-DE-58. ASME Design Engineering Conference. New York，1967.

[2]Seager D L. Conditions for the neutralization of excitation by the teeth in epicyclic gearing [J]. Journal Mechanical Engineering Science，1975, 17(5): 293—298.

[3]Kahraman A. Natural modes of planetary gear trains [J]. ASME Journal of Sound and Vibration, 1994, 173(1): 125—130.

[4]Kahraman A. Planetary gear train dynamics [J]. ASME Journal of Mechanical Design, 1994, 116(3): 713—720.

[5]Kahraman A, Blankenship G W. Planet mesh phasing in epicyclic gear sets[C]. In: International Gearing Conference. Newcastle, UK, 1994：99—104.

[6]Parker R G. A physical explanation for the effectiveness of planet phasing to suppress planetary gear vibration [J]. Journal of Sound and Vibration, 2000, 236(4): 561—573.

[7]Parker R G, Agashe V, Vijayakar S M. Dynamic response of a planetary gear system using a finite element/contact mechanics model [J]. ASME Journal of Mechanical Design, 2000, 122(3): 304—310.

[8]Parker R G, Lin J. Mesh phasing relationships in planetary and epicyclic gears [J]. ASME Journal of Mechanical Design, 2004, 126(2): 365—370.

[9]Ambarisha V K, Parker R G. Suppression of planet mode response in planetary gear dynamic through mesh phasing [J]. ASME Journal of Vibration and Acoustics, 2006, 128(2): 133—142.

[10]Ambarisha V K, Parker R G. Nonlinear dynamics of planetary gears using analytical and finite element models [J]. Journal of Sound and Vibration, 2007, 302(3): 577—595.

[11]Wu X U. Vibration of planetary gears having an elastic continuum ring gear[D]. Ohio State University, 2010.

[12]秦大同，肖正明，王建宏．基于啮合相位分析的盾构机减速器多级行星齿轮传动动力学特性 [J].机械工程学报，2011，47(23)：20—28．

Qin D T, Xiao Z M, Wang J H. Dynamic characteristics of multi-stage planetary gears of shield tunnelling machine based on planet mesh phasing analysis[J]. Journal of Mechanical Engineering, 2011, 47(23): 20—28.

[13]肖正明，秦大同，尹志宏.多级行星齿轮系统耦合动力学分析与试验研究[J].机械工程学报，2012，48(23)：51—58．

Xiao Z M,Qin D T, Yin Z H. Multi-stage planetary gears dynamic coupling analysis and experimental investigation[J]. Journal of Mechanical Engineering, 2012, 48(23): 51—58.

[14]段福海，郭飚，胡青春，等.齿轮中心双流传动系统的动力学分析 [J].华南理工大学学报(自然科学版)，2008，36(8)：117—122．

Duan F H, Guo B, Hu Q C, et al. Dynamic analysis of two path and load share sun geared system[J]. Journal of South China University of Technology (Natural Science Edition), 2008, 36(8): 117—122．

[15]王世宇.基于相位调谐的直齿行星齿轮传动动力学理论与实验研究 [D]. 天津：天津大学，2005．

Wang S Y. Theoretical and experimental investigation on dynamics of spur planetary gear transmissions based on planet phasing theory [D]. Tianjin: Tianjin University, 2005.

[16]Stockton R J. Sun gear traveling wave vibration in a sequential planetary gearbox[C]. In: ASME Design Engineering Division Conference and Exhibit on Mechanical Vibration and Noise． Cincinnati, Ohio, USA, 1985, 85-DET-167.

[17]Talbert P B. Generalized excitation of traveling wave vibration in gears[C]. In: American Gear Manufacturers Association Conference. Technical Paper No. 04FTM08, 2004.

[18]Canchi S V, Parker R G. Effects of ring-planet mesh phasing and contact ratio on the parametric instabilities of a planetary gear ring [J]. ASME Journal of Mechanical Design, 2008, 130(1): 014501.

[19]Wang S Y, Huo M N, Zhang C, et al. Effect of mesh phase on wave vibration of spur planetary ring gear [J]. European Journal of Mechanics-A/Solids, 2011, 30(6): 820—827.

[20]Chen D L, Wang S Y, Xiu J, et al, Physical explanation on rotational vibration via distorted force field of multi-cyclic symmetric systems[C]. 13th World Congress in Mechanism and Machine Science (IFToMM′11). Guanajuato, Mexico, 2011, June 19—25.

[21]Huo M N, Wang S Y, Xiu J, et al. Effect of magnet/slot combination on triple-frequency magnetic force and vibration of permanent magnet motors[J]. Journal of Sound and Vibration, 2013, 332(22): 5965—5980.

[22]Wang S Y, Xiu J, Cao S Q, et al. Analytical treatment with rigid-elastic vibration of permanent magnet motors with expanding application to cyclically symmetric power-transmission systems[J]. ASME Journal of Vibration and Acoustics, 2014, 136(2): 021014.

[23]Vantsevich V V. Force vibrations in automotive bevel gear differentials[C]. Noise & Vibration Conference and Exhibition. Traverse City, Michigan, May 5-8, 2003.

[24]王世宇，王建，曹树谦，等，锥齿行星齿轮传动模态特性分析 [J].振动工程学报，2011，24(4)：376-384．

Wang S Y, Wang J, Cao S Q, et al. Modal properties for bevel planetary gear trains [J]. Journal of Vibration Engineering, 2011, 24(4): 376—384.

[25]方宗德，沈允文，黄镇东．三路功率分流恒星式减速器的动态特性[J]．航空动力学报，1990，11(7)：341—350．

Fang Z D, Shen Y W, Huang Z D. The dynamic behavior of star gearing with three branches[J]. ACTA Aeronatutica Et Astronatutica Sinica, 1990, 11(7): 341—350.

[26]Yang J M, Zhang C, Lin Z Q, et al. Theoretical explanation for lower order harmonic resonance phenomenon of three-ring gear transmissions[J]. Journal of Shanghai Jiaotong University, 2003, E-8(1): 71—74.

[27]Han Q K, Wang J J, Li Q H. Spectral properties for the vibration response of parametrically excited system[J]. Archive of Applied Mechanics, 2010, 80(6): 671—685.

[28]Wang S Y, Sinha S C. Parametric instability in a gear train system due to stiffness variation[C]. ASME International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Portland, Oregon, USA, 2013.

Planet phasing of bevel planetary gear trains

XIEBang1,WANGShi-yu1,2,3

(1.School of Mechanical Engineering, Tianjin University, Tianjin 300072, China;2.Key Laboratory of Mechanism Theory and Equipment Design of Ministry of Education, Tianjin University,Tianjin 300072, China;3.Tianjin Key Laboratory of Nonlinear Dynamics and Chaos Control, Tianjin 300072, China)

This work analyzes the effect of meshing phase on vibration behaviors by using the structural and force symmetries of the bevel planetary gear trains. The relationships between the basic parameters, including the number of the central gear tooth, the number of the planet gears, and the force and vibration are obtained. The results imply that the vibration can be classified into three typical groups: axial-translational androtational modes, where the central components exhibit translational motion and rotational motion about their axes, radial-translational and torsional modes, where the central components exhibit translational motion and torsional motion about the two axes perpendicular to the rotational axis, and force balanced modes, where the central components are stationary. The analytical prediction and its effectiveness on the vibration reduction are verified by numerical calculation and comparison with the existing literature.

bevel planetary gear trains； time-varying meshing stiffness； planet phasing； vibration modes

2014-06-01；

2015-11-04

国家自然科学基金资助项目(51175370);天津市应用基础与前沿技术研究计划重点项目(13JCZDJC34300)

TH113.1;TH132.425

A

1004-4523(2016)01-0069-09

10.16385/j.cnki.issn.1004-4523.2016.01.010

谢帮(1989—)，男,硕士研究生。E-mail： xbalex1989@163.com

王世宇(1974—),男，博士，副教授。E-mail:wangshiyu@tju.edu.cn