利用有限元法与打靶法的纵横耦合轴系主共振分析*

邹冬林， 刘　翎，饶柱石， 塔　娜

(1.上海交通大学振动、冲击、噪声研究所，上海 200240；2.上海交通大学机械系统与振动国家重点实验室，上海 200240)



利用有限元法与打靶法的纵横耦合轴系主共振分析*

邹冬林1，2， 刘翎1,2，饶柱石1,2， 塔娜1,2

(1.上海交通大学振动、冲击、噪声研究所，上海 200240；2.上海交通大学机械系统与振动国家重点实验室，上海 200240)

在考虑Von Karman非线性位移-应变关系下，利用Hamilton原理与有限元方法建立了轴系纵横耦合非线性动力学模型， 推导了其非线性刚度矩阵。结合打靶法研究了轴系在外激励下的横向主共振响应及其稳定性。探讨了激励载荷、阻尼比以及细长比对轴系纵横耦合效应的影响。研究表明：纵横耦合效应呈“硬弹簧”特性，使幅频响应曲线向右倾斜；在某些激励频率处，幅频响应曲线上存在多个稳定解，从而使幅值出现跳跃现象；激励载荷越大，阻尼比越小，细长比越小，系统纵横耦合效应越强；增加阻尼比可以有效抑制纵横耦合非线性效应，提高轴系的稳定性。分析结果对轴系的设计有指导意义。

非线性振动； 纵横耦合轴系； 有限元； 打靶法； 主共振

引　言

在许多工程机械中，旋转轴系常被用来传递动力，起着非常重要的作用。例如船舶推进轴系，飞机发动机轴系以及汽轮机轴系等等。轴系运转时不可避免地产生振动，从而降低机器的工作效率，严重时会使轴系断裂，造成事故。随着科学技术的进步，轴系的结构越来越复杂，载荷也越来越大，轴系振动问题越来越突出。因此对轴系的动力学分析一直是国内外研究的热点。轴系的振动分为3种形式：弯曲振动、扭转振动以及纵向振动。早期对轴系的研究都是对这3种振动单独处理，这样处理有利于模型的简化。然而对一些处于复杂工况的轴系，各种运动之间有相当强的耦合，分开处理不能揭示工程中的一些现象，比如出现多频现象，发生组合共振、自激振动及分岔现象等等。近年来，针对弯扭耦合振动的研究文献很多，大多数均以齿轮轴系或汽轮机轴系等为研究对象[1-2]。但是针对轴系弯纵耦合振动的研究文献还相当少，主要原因是这两种振动之间的耦合在工程中不常见。而对于大跨度轴系(例如船舶推进轴系，一般长度为十几米甚至几十米)或细长轴系，由于细长比很小(细长比指轴系截面回转半径与轴系长度之比)，当激励力较大时，容易引起轴系较大振动。此时横向振动很大，进而其纵、横向之间的弹性耦合效应也很强。当轴系纵、横向间产生非线性耦合振动时，可能会伴有能量渗透、饱和等现象，从而使轴系某些方向上振动进一步加强，使轴系振动过大而产生裂纹。同时尽管在轴系设计时已使工作频率避开了轴系的共振频率，但是因为这种设计并没有考虑纵、横耦合效应的影响，而纵、横向间的非线性耦合效应会改变轴系的固有频率，这时工作频率有可能落在共振频率段，并产生主共振、超谐共振及亚谐共振等现象，使轴系振动剧烈。因此研究轴系纵、横耦合效应时的动力学特性有重要的实际意义。

目前对于轴系纵横耦合的研究，国内文献非常少。有不少学者针对平面梁结构纵横耦合振动问题做过研究[3-5]，但是转子结构与梁结构间最显著的差别是转子结构有旋转而产生的陀螺效应，从而使转子振动产生新的现象，比如正进动与反进动等。近十年来，国外对轴系纵横耦合非线性动力学进行了大量研究。Khadem与Hossein团队在这一领域做了许多贡献。他们研究了纵横耦合作用下可伸长与不可伸长轴系的自由振动响应[6-7]；研究了不可伸长轴系的主共振响应[8-9]以及可伸长轴系的主共振与参数共振响应[10-11]；研究了不可伸长轴系两阶模态间的联合共振[12-13]以及分叉与稳定性问题[14]。Ishida团队也做了类似的工作[15-17]。但是在这些团队的研究中，存在两个问题：首先他们均认为轴系纵向惯性可以忽略，这样可以对纵横耦合动力学方程进一步简化以便研究。由于他们研究的对象都是简支轴系，纵向固有频率远高于横向固有频率，因此这种简化是合理的。但是对于多支承多盘轴系，如船舶推进轴系，由于螺旋桨集中质量以及推力轴承的影响，纵向惯性效应很显著，直接忽略会带来误差。其次他们的研究思路是：利用Galerkin法(权函数采用一阶模态振型)，将偏微分方程转化为常微分方程，再利用多尺度法或者谐波平衡法或者平均法求解方程的一次近似解。或者基本解取为一阶模态振型，直接利用多尺度法求解偏微分方程。这两处理方法的理论基础是“单模态共振理论”[18]。即当多自由度非线性系统进入共振状态时，系统运动主要由所涉及的各阶单一主模态所控制。因此这两方法只能分析各种共振响应。而对于非共振响应，这两种处理方法均由于模态截断而产生误差。同时由于计算的复杂性，采用多尺度法时一般只取两个时间尺度，求取一次近似解，很难获得系统的高次近似解。

随着电子计算机及计算技术的发展，高精度的数值计算得到了广泛应用。有限元方法由于其通用性强以及精度高的特点，常常被用来研究大型复杂结构动力学分析。配合Newmark法、Wilson-θ法等直接数值积分方法，可以很方便地处理非线性振动问题[19]。然而这些方法在求取非线性系统周期解时非常依赖于初始条件的选取，如果初始条件选择不当，很难获得稳态的周期解。同时当系统存在多解时，这些方法通常只能求取稳定解。近年来，有学者利用有限元法结合谐波平衡法求取系统的周期解[20]。其基本思想是先假定解由一系列谐波级数组成，代入有限元方程后取两边相同谐波级数的系数相等，从而得到关于各谐波系数的非线性代数方程组。这种处理方法的缺陷是当假定解的谐波级数很高时，非线性代数方程维数很大，很难求解；而谐波级数很少时，解的精度又得不到保证。

近年来又有不少学者利用打靶法求解系统的周期响应[21-22]。打靶法基本思想是把求解边值问题转化为求解初值问题。它既可以求系统的稳定解也可以求其非稳定解。同时利用打靶法时所产生的单值矩阵可以判断解的稳定性。因此打靶法成为研究非线性振动的有效方法之一。

综上所述，本文采用限元法建立轴系纵横耦合动力学模型，理论上考虑了所有的线性模态，因而不存在模态截断误差，既可以分析共振响应，也可以分析非共振响应。同时结合打靶法既可以求解稳定周期解，也可以求非稳定周期解。

本文在考虑纵向惯性作用下，采用有限元法建立轴系纵横耦合非线性动力学模型，推导其非线性刚度矩阵，结合打靶法研究轴系的横向主共振响应(所谓主共振是指外激励频率等于其固有频率)，探讨激励载荷、阻尼比以及细长比对轴系纵横耦合效应的影响。

1　有限元动力学模型

本文以具有多线性支承及集中质量的船舶推进轴系为分析对象，其余轴系结构也可以类似处理。典型的船舶推进轴系由螺旋桨、3个径向轴承以及推力轴承组成，如图 1所示。为了简化分析，假设轴系具有均匀截面，螺旋桨简化为集中质量(考虑转动惯量影响)，各轴承模型忽略交叉刚度与阻尼的影响，仅考虑径向刚度的影响(轴承阻尼用模态阻尼等效)，简化为线性弹簧单元。本文的目的是考察轴系发生纵横耦合几何非线性时的动力学特性，为了聚焦轴系在这种几何非线性下所特有振动特性，因此忽略了轴承的非线性以排除其他非线性源的干扰。同时这样做也简化了分析问题。

图1　船舶推进轴系简图Fig.1　Schematic of marine propulsion shafting

用空间梁单元模拟轴系的纵、横向振动； 使用2节点梁单元，单元长度L，每个节点5个自由度，即纵向位移u，垂直位移v和转角θy，水平位移w和转角θz。采用瑞利梁模型(考虑转动惯量忽略剪切变形的影响)，并考虑Von Karman非线性位移-应变关系[23]。则单元轴段的应变势能和动能可以写成

(1)

式中前两项为线性应变能，后两项为弯纵耦合引起的非线性应变能。其中，E为弹性模量；A为轴段截面积；Id为截面惯性矩。

(2)

纵向位移采用线性函数作为插值函数，横向位移采用一阶Hermite函数作为插值函数[24]。代入式(2)中，可以得到单元的质量矩阵Me与陀螺矩阵Ge。

(3)

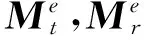
代入式(1)中，可以得到单元的刚度矩阵Ke。

(4)

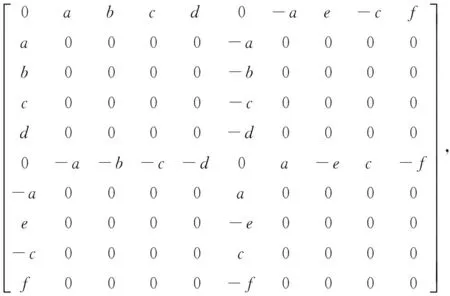
把单元质量矩阵、单元陀螺矩阵以及单元刚度矩阵组装后，并考虑集中质量以及支撑弹簧的影响，同时加入阻尼的影响，得到轴系纵横耦合振动方程

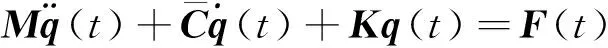
(5)

2　打靶法

接下来用打靶法[25]求解式(5)的周期解。求微分方程的周期解，数学本质是求解边值问题。打靶法是求解边值问题的常用数值方法。“打靶”是一种形象说法，把解的曲线看作是“子弹”的轨迹，从一端发射“子弹”，将另一端看作“靶子”，利用“靶子”的位置来调整一些“子弹”的发射参数(即初始条件)，从而获得所需的轨迹[26]。刘恒等针对转子动力学中遇到的各种问题，利用打靶法并结合其他数值方法研究了转子系统的周期解及稳定性边界和分叉形式[27-31]，取得了良好的效果。

引入变量X(t)={y(t),q(t)}T，将式(5)转化为一阶方程组

(6)

求系统的周期解，实质就是寻求解，使之满足

(7)

式中T为周期，取T=2π/Ω。

设X(0)=s，则打靶法的求解过程就是寻找合适的s，使得残差为零。即

(8)

可以采用Newton迭代法来求解式(5)，将其在第i次近似值si附近展开成泰勒级数，取其线性部分

(9)

上式可进一步转化为

(10)

式中J(si)为r(s)对s的Jacobian矩阵。其计算公式为

(11)

将式(6)两边对s求导数：

(12)

由式(12)可知，W即为该矩阵微分方程初值问题的解在t=T时的值。

联立求解式(6)与式(12)，可以求出X(T)与W，从而可以按式(8)判断残差r(s)，若残差接近零，则计算结束，否则按式(10)更新s，一直迭代下去。

周期解的稳定性判别采用Floquet理论[25]，通过求解周期解状态转移矩阵W的特征值(又称为Floquet乘子)来进行。当所有Floquet乘子均位于复平面单位圆内时，则周期解稳定。

为了得到系统的幅频响应曲线，求解时，每次给定一个转速，从而确定周期T，得到该转速下的周期解后，再增加转速，依次求得不同转速下的周期解，从而得到系统的幅频响应曲线。为了更突出共振频率处系统的响应特性，把求解的初始转速与终止转速设在共振频率附近。

3　实例分析

以工程中的某一船舶推进轴系为算例，轴系长度14.5 m，外径220 mm，内径100 mm，轴系细长比s=0.0041，材料弹性模量210 GPa，密度7800 kg/m3。轴系各支承参数：后艉轴承径向刚度2.5×108N/m；前艉轴承径向刚度0.8×108N/m；中间轴承径向刚度3×108N/m；推力轴承刚度3×108N/m。螺旋桨为7叶桨，其质量为6t，直径转动惯量为3000 kg·m2。

主共振响应是指外激励频率等于其固有频率的响应[32]。相应的还有超谐共振与亚谐共振。N次超谐共振是指N倍激励频率等于其固有频率。1/N次亚谐共振是指1/N倍激励频率等于其固有频率。由于本文是以船舶推进轴系为算例，因此有工频(旋转速度)和叶频(旋转速度乘叶片数)两种激励频率。因为螺旋桨为7叶桨，所以一倍叶频为工频的7倍。当轴系一倍叶频等于横向第1阶固有频率时，此时若只把工频作为外激励频率，则称之为7次超谐共振[33]。若把工频与一倍叶频看成两个外激励频率，则称之为主共振。因此本文把工频与叶频看成是两个外激励频率。对于一般轴系，由于只有工频，则不存在这个问题，统一称为主共振。

图 2是用有限单元法(将轴系划分成260节点)求得线性下横向第1阶正反进动频率随转速的变化趋势。图中7Ω线与正进动的交点即为横向第1阶固有频率，为6.13 Hz。

图2　第1阶正反进频率随转速变化Fig.2　Change of the first forward and backward frequency vs rotation speed

为了简化，计算时假设螺旋桨处的纵向激励载荷为0，仅考虑螺旋桨处的横向激励载荷，其值分别取为1000与2000 N两种工况。

将阻尼假设为刚度比例阻尼，即

(13)

式中K1为线性刚度矩阵；β为比例系数，按下式计算

(14)

式中ω1为横向第1阶线性固有频率；ξ1为第1阶振型阻尼比，本文取其值为0.005,0.01与0.02三种工况分别计算。将阻尼假设为刚度比例阻尼的优点是可以有效消除高阶振型对系统响应的影响[34]。

为了更突出共振频率附近轴系的频响特性，只选取横向第1阶固有频率附近几个频率点计算。由于响应中存在多频分量，对于每一频率点，对周期响应作FFT分析，只提取工频幅值分析。

打靶法在求取不稳定周期解时，对初值要求很高，因此有些研究者对打靶法进行了改进以扩大其收敛域[35]。本文采用插值与试探方法来确定初值。以图 3为例，将求解区域分成AB、BC、EF及ED几个区间。求解时先从A点开始一直求解到C点，接着从F点开始，求解到E点，最后从E点开始求解到D点。由于AB段及F以右段和线性解差别不大，且有唯一解，因此这两个区域的迭代初值很容易收敛，不难确定，因此可以试探进行(也可以用线性解作为试探值)。求BC段时，由于BC段是AB段的近似直线延伸，可以选取AB段上两个已求取的点(紧邻待求点)，以待求点的频率为自变量，线性插值后求得待求点的幅值作为其迭代初始值；类似地，EF段也采用线性插值法；ED段由于拐角处曲率变化较大，且其形状近似与EF段关于某一直线对称，因此可采用抛物线插值。首先在EF段上选取两个已求取的点，同时抛物线的顶点(对称轴)近似取在拐角点处，从而求得待求点的幅值作为迭代初值。而在选取EF段上的已求取点时，为保证更好的收敛性，可以通过对曲线形状的预估尽量选择与待求点关于顶点对称的点。尽管采用如此方法，计算表明求取ED段个别点时仍不收敛，这时可以更换EF段上的点或抛物线的对称轴可以解决问题。当ED段求取了两个以上点时，也可以采用线性插值求其余的点。速度也做类似插值处理。

图 3是载荷为2000 N,第1阶振型阻尼比为0.01时的幅频响应曲线。从图中可以得出：纵横耦合效应呈“硬弹簧”特性使共振时的频率略大于线性固有频率，同时在某些频率点处响应存在3个解(两个稳定解和一个不稳定解)，从而使轴系升速与降速时响应出现跳跃现象。

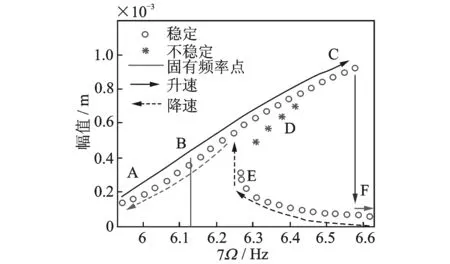
图3　F=2000 N，ξ1=0.01时幅频响应曲线Fig.3　Frequency response curve when F=2000 N，ξ1=0.01

图4是利用作者发表的文献[33]中所采用的多尺度法与本文方法所得结果进行比较，以验证本文方法的有效性。从图中可以看出，多尺度法的结果与本文结果整体趋势是一致的，都有跳跃现象。但是多尺度法的结果的幅值比本文方法略小。可能原因有两点，一是文献中的多尺度法只求取一次近似解，忽略了高次近似解；二是多尺度法只考虑了一阶模态振型函数，忽略了高阶振型的影响。

图4　本文方法与多尺度法结果对比Fig.4　The comparison between our method and multiple scale method

图 5是载荷为1000 N,第1阶振型阻尼比为0.01时的幅频响应曲线。图 6是载荷为2000 N,第1阶振型阻尼比为0.02时的幅频响应曲线。图 7是载荷为1000 N,第1阶振型阻尼比为0.02时的幅频响应曲线。图 8是载荷为2000 N,第1阶振型阻尼比为0.005时的幅频响应曲线。图 9是载荷为1000 N,第1阶振型阻尼比为0.005时的幅频响应曲线。通过这几个图的比较可以得出：载荷越大，阻尼比越小时，纵横耦合效应越强。同时可以得出：阻尼比对非线性的影响很大。从图 7可以得出，当阻尼比很大时，尽管系统的共振频率仍略大于其线性固有频率，但是此时系统已经不存在不稳定解。因此增加轴系的阻尼可以有效抑制纵横耦合效应，同时使轴系变得更稳定。

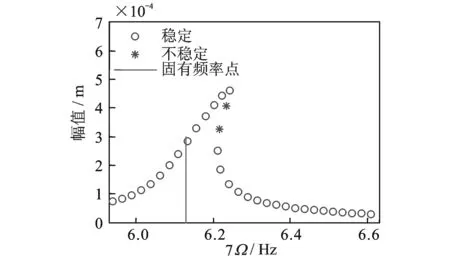
图5　F=1000 N，ξ1=0.01时幅频响应曲线Fig.5　Frequency response curve when F=1000 N，ξ1=0.01

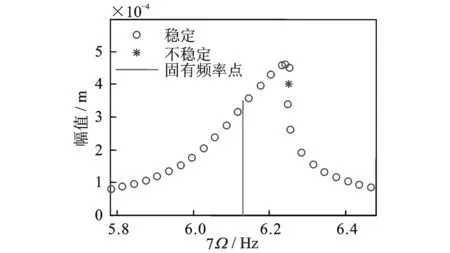
图6　F=2000 N，ξ1=0.02时幅频响应曲线Fig.6　Frequency response curve when F=2000 N，ξ1=0.02

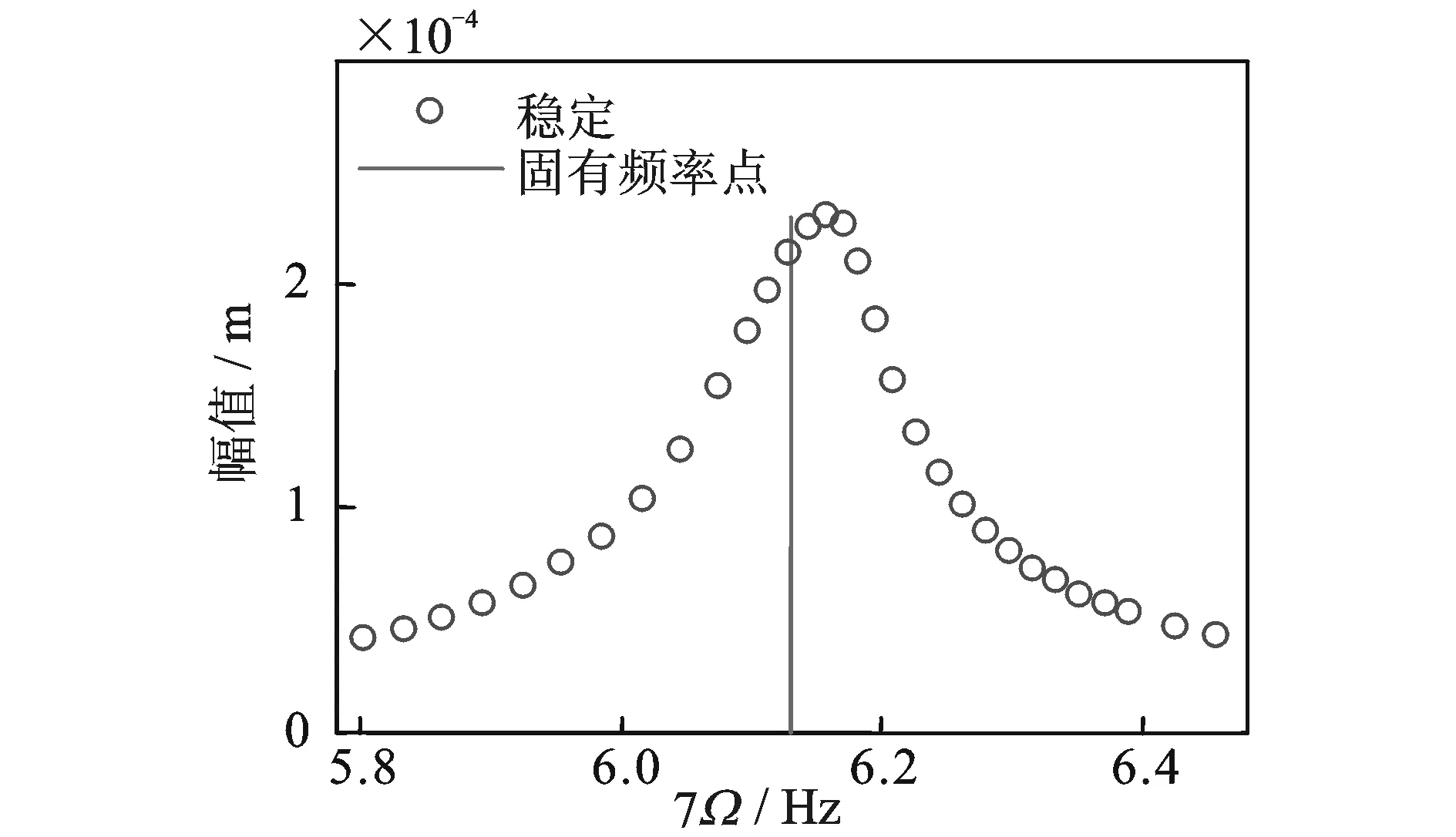
图7　F=1000 N，ξ1=0.02时幅频响应曲线Fig.7　Frequency response curve when F=1000 N，ξ1=0.02

图8　F=2000 N，ξ1=0.005时幅频响应曲线Fig.8　Frequency response curve when F=2000 N，ξ1=0.005

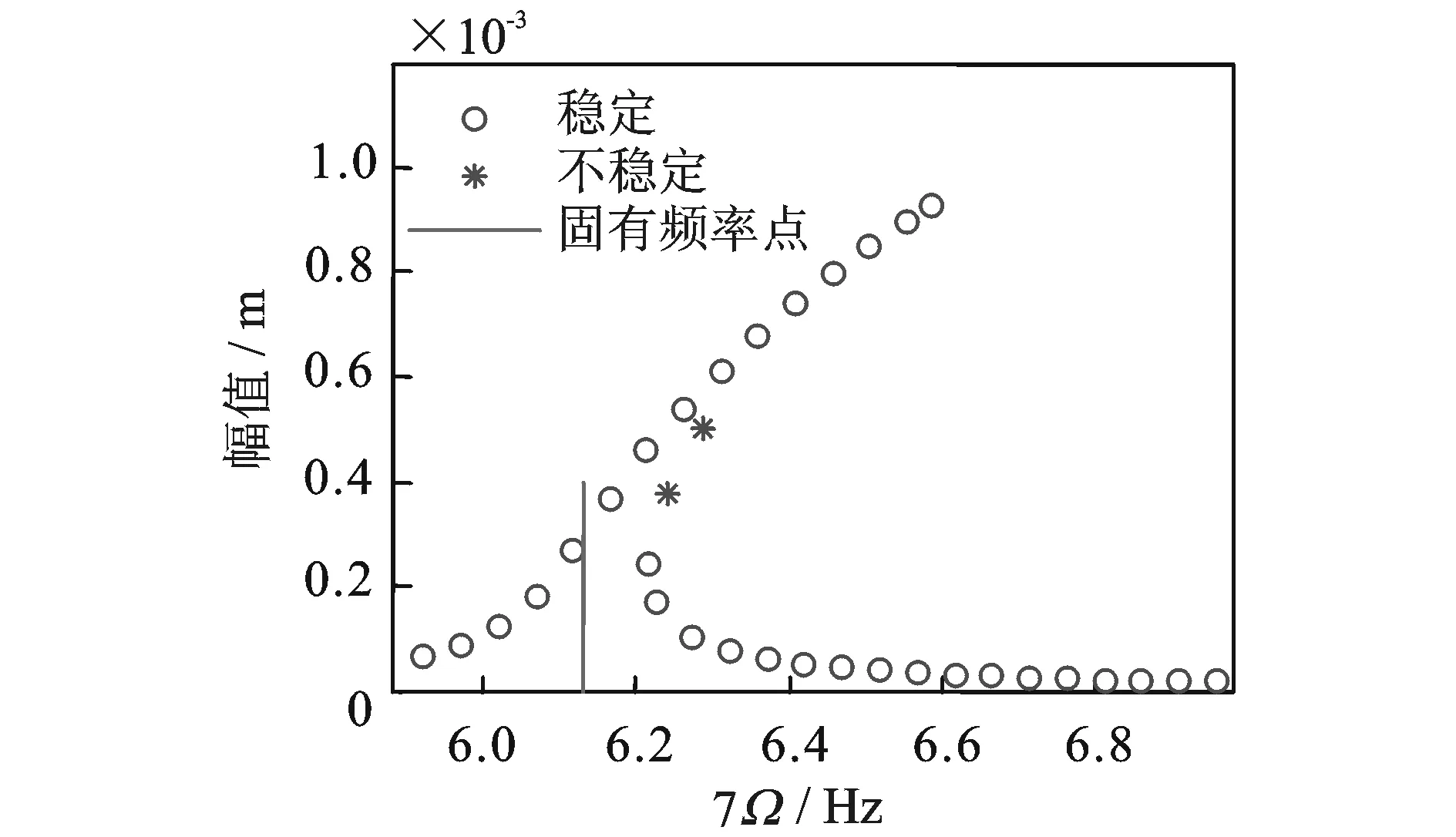
图9　F=1000 N，ξ1=0.005时幅频响应曲线Fig.9　Frequency response curve when F=1000 N，ξ1=0.005

若把轴系的外径变为240 mm，内径变为120 mm，其余参数不变。此时轴系细长比s=0.0046，横向第1阶固有频率相应变为7.11 Hz。对此轴系进行同样的计算。

图 10是载荷为2000 N,第1阶振型阻尼比为0.01时的幅频响应曲线。图 11是载荷为1000 N,第1阶振型阻尼比为0.01时的幅频响应曲线。图 12是载荷为2000 N,第1阶振型阻尼比为0.005时的幅频响应曲线。图 13是载荷为1000 N,第1阶振型阻尼比为0.005时的幅频响应曲线。分别与图3,5,8和9比较可知，细长比越小时，轴系纵横耦合效应越强。

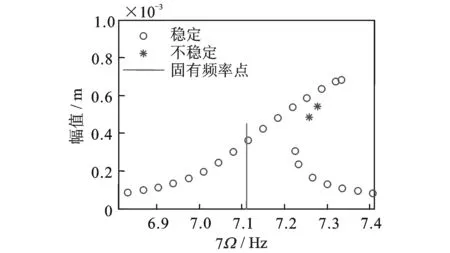
图10　F=2000 N，ξ1=0.01时幅频响应曲线Fig.10　Frequency response curve when F=2000 N，ξ1=0.01

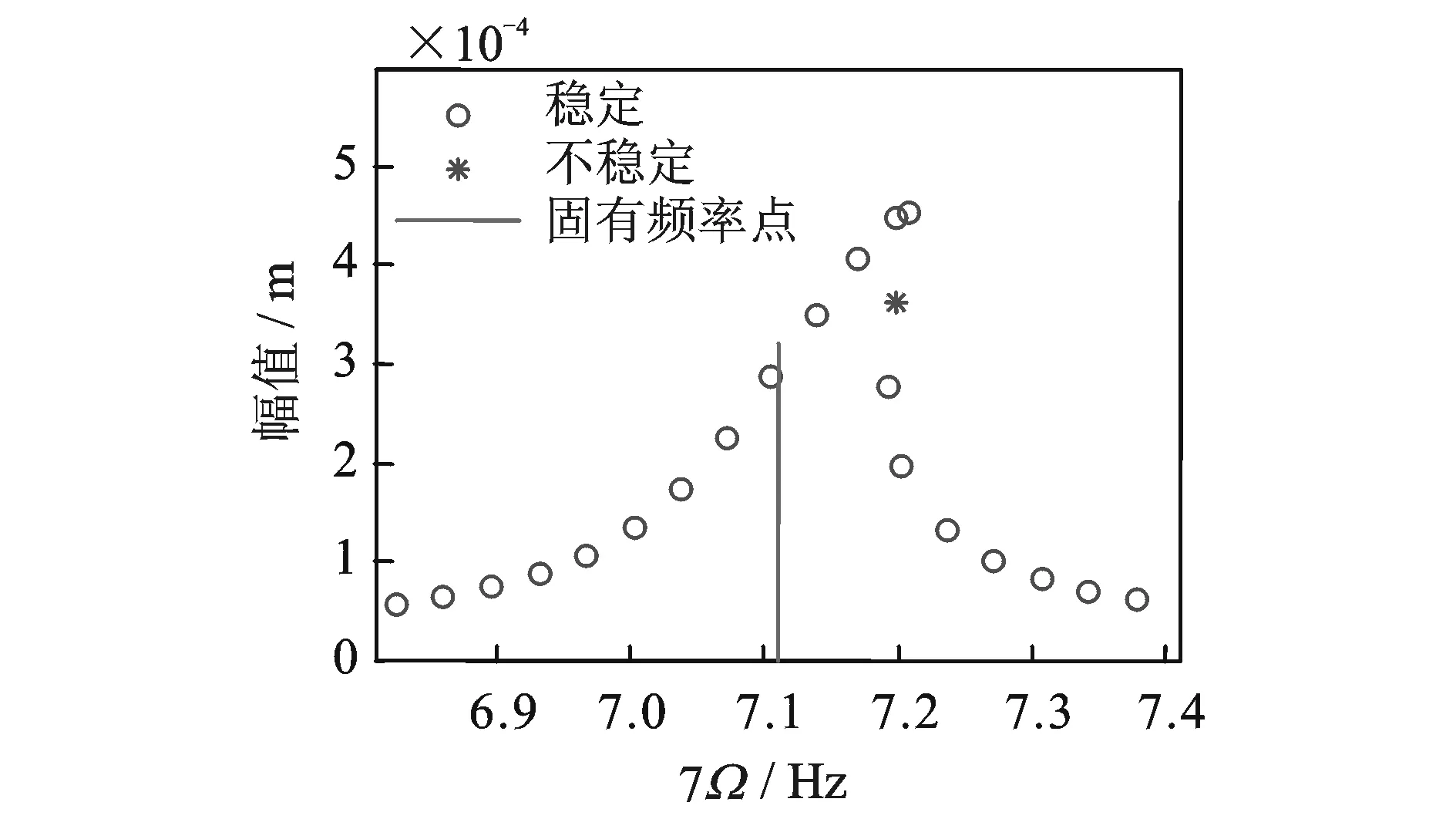
图11　F=1000 N，ξ1=0.01时幅频响应曲线Fig.11　Frequency response curve when F=1000 N，ξ1=0.01

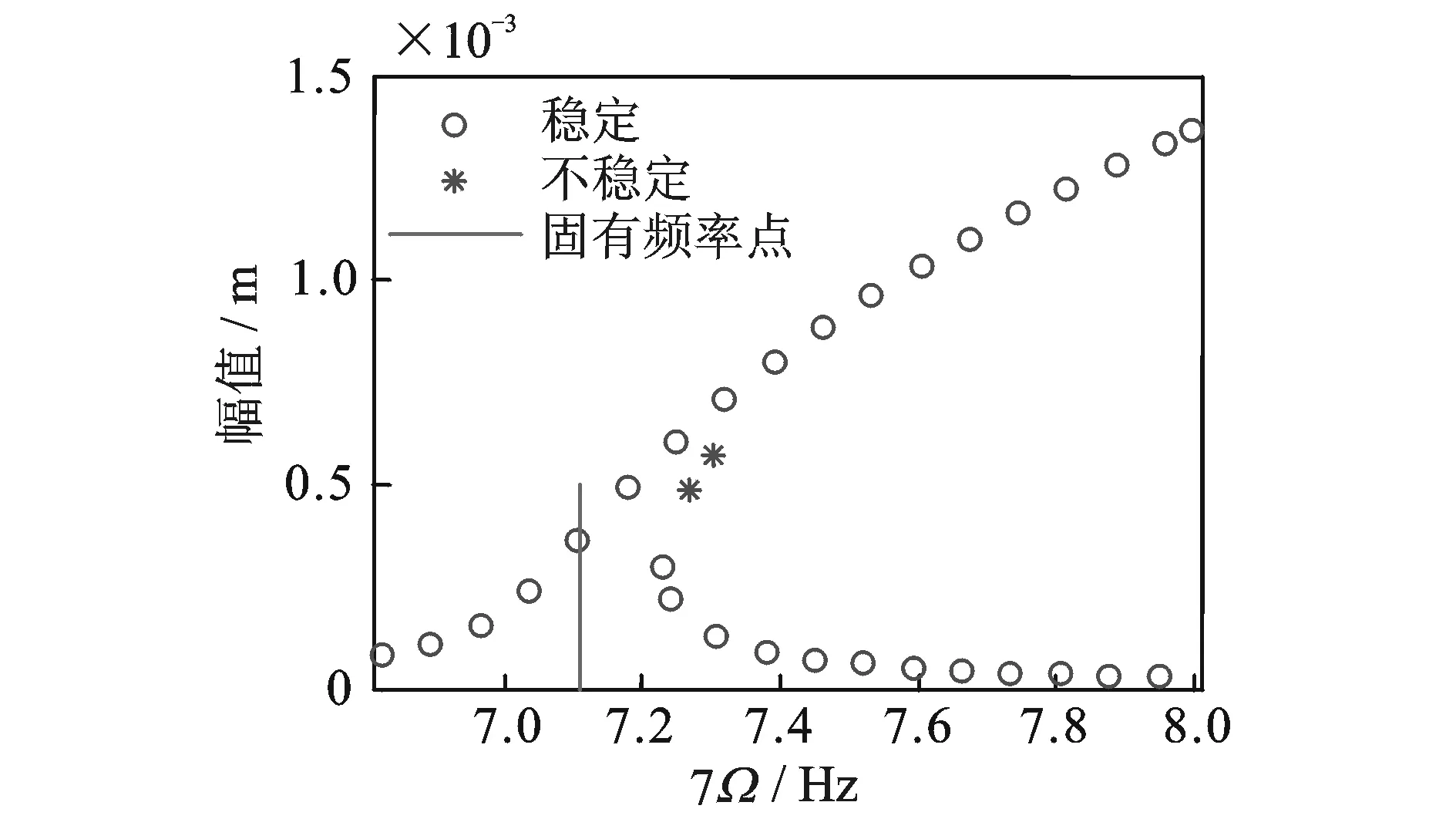
图12　F=2000 N，ξ1=0.005时幅频响应曲线Fig.12　Frequency response curve when F=2000 N，ξ1=0.005

图13　F=1000 N，ξ1=0.005时幅频响应曲线Fig.13　Frequency response curve when F=1000 N，ξ1=0.005

4　结　论

打靶法是求解非线性系统周期解的一种有效方法，本文利用打靶法结合有限元法求解了轴系纵横耦合效应下横向主共振响应，探讨了激励载荷、阻尼比以及细长比对轴系纵横耦合效应的影响。研究表明：

(1)轴系发生纵横耦合效应时，这种非线性呈“硬弹簧”效应，使共振时的固有频率大于其线性固有频率。

(2)在某些频率点处，幅频响应曲线存在多解，使响应出现跳跃现象。

(3)激励载荷越大，阻尼比越小，细长比越小时，轴系纵横耦合效应越强；

(4)增加阻尼比可以有效抑制这种几何非线性效应，并提高轴系的稳定性。

这些结论对轴系的设计具有指导意义。因此在实际的轴系设计中，对于大跨度细长轴系，为了更精确的预测其固有频率，应考虑纵横耦合效应所产生的影响。这种耦合效应会适当增加轴系固有频率。而对于容易发生纵横耦合效应的细长轴系，适当增加阻尼比可以有效抑制这种非线性效应，提高轴系的稳定性。

[1]陈予恕, 李军. 汽轮发电机组轴系弯扭耦合振动问题研究综述[J]. 汽轮机技术, 2012, 54(3):161—164.

Chen Yushu, Li Jun. Research on bending-torsion coupling vibration of shaft of turbine generator[J]. Turbine Technology, 2012, 54(3):161—164.

[2]夏伯乾, 虞烈, 谢友柏. 齿轮-转子-轴承系统弯扭耦合振动模型研究[J]. 西安交通大学学报, 1997, 31(12):95—101.

Xia Boqian, Yu Lie, Xie Youbai. Study on lateral-torsional coupling vibration model of gear-rotor-bearing system[J]. Journal of Xi′an Jiaotong University, 1997, 31(12): 95—101.

[3]胡义, 杨建国. 梁纵横耦合振动研究[J]. 武汉理工大学学报(交通科学与工程版), 2010, 34(03): 537—541.

Hu Yi, Yang Jianguo. Studies on the longitudinal and lateral coupled vibration of beam[J].Journal of Wuhan University of Technology(Transportation Science & Engineering), 2010, 34(03): 537—541.

[4]夏品奇. 纵横向耦合梁的谐波响应分析[J]. 振动工程学报, 1995, 8(1): 67—72.

Xia Pinqi. Harmonic response of beam with longitudinal and transversal coupling[J].Journal of Vibration Engineering, 1995, 8(1): 67—72.

[5]易壮鹏, 赵跃宇, 朱克兆. 梁的纵向与横向耦合振动的动力学分析[J]. 应用力学学报, 2008, 25(04): 687—692,740.

Yi Zhuangpeng, Zhao Yueyu, Zhu Kezhao. Dynamic analysis of beams with longitudinal and transversal coupled vibration[J]. Chinese Journal of Applied Mechanics, 2008, 25(04): 687—692,740.

[6]Hosseini S A A, Khadem SE. Free vibrations analysis of a rotating shaft with nonlinearities in curvature and inertia[J]. Mechanism and Machine Theory, 2009, 44:272—288.

[7]Hosseini S A A, Zamanian M. Multiple scales solution for free vibrations of a rotating shaft with stretching nonlinearity[J]. Scientia Iranica, 2013, 20:131—140.

[8]Hosseini S A A, Zamanian M, Shams S, et al. Vibration analysis of geometrically nonlinear spinning beams[J]. Mechanism and Machine Theory, 2014, 78:15—35.

[9]Khadem S E, Shahgholi M, Hosseini SAA. Primary resonances of a nonlinear in-extensional rotating shaft[J]. Mechanism and Machine Theory, 2010, 45:1067—1081.

[10]Shahgholi M, Khadem S E, Primary and parametric resonances of asymmetrical rotating shafts with stretching nonlinearity[J]. Mechanism and Machine Theory, 2012, 51:131—144.

[11]Hosseini S, Khadem S. Analytical solution for primary resonances of a rotating shaft with stretching non-linearity[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2008, 222:1655—1664.

[12]Hosseini S A A, Khadem S E. Combination resonances in a rotating shaft[J]. Mechanism and Machine Theory, 2009, 44:1535—1547.

[13]Khadem S E, Shahgholi M, Hosseini S A A. Two-mode combination resonances of an in-extensional rotating shaft with large amplitude[J]. Nonlinear Dynamics, 2011, 65:217—233.

[14]Hosseini S A A. Dynamic stability and bifurcation of a nonlinear in-extensional rotating shaft with internal damping[J]. Nonlinear Dynamics, 2013, 74:345—358.

[15]Ishida Y, Yamamoto T, Ikeda T. Nonlinear forced oscillations caused by quartic nonlinearity in a rotating shaft system[J]. Journal of Vibration and Acoustics, 1990, 112:288—297.

[16]Ishida Y, Nagasaka I, Inoue T, et al. Forced oscillations of a vertical continuous rotor with geometric nonlinearity[J]. Nonlinear Dynamics, 1996, 11:107—120.

[17]Ishida Y, Inoue T. Internal resonance phenomena of an asymmetrical rotating shaft[J]. Journal of Vibration and Control, 2005, 11:1173—1193.

[18]郑兆昌. 关于线性和非线性系统内在的本质联系——多自由度非线性系统的定量和定性分析[J]. 振动与冲击, 2008,(01): 4—8,178.

ZHENG Zhaochang. Interinsic and smple connection of linear systems with non-linear quantitative and qualitative analysis of large scale multiple dof nonlinear systems[J]. Journal of Vibration and Shock, 2008,(01): 4—8,178.

[19]陈玲莉. 工程结构动力分析数值方法[M]. 西安: 西安交通大学出版社, 2006.

[20]Lewandowski. Computational formulation for periodic vibration of geometrically nonlinear structures-part 1: Theoretical background[J]. International Journal of Solids and Structures, 1997, 34(15):1925—1947.

[21]Sundararajan P, Noah S T. Dynamics of forced nonlinear systems using shooting/arc-length continuation method-application to rotor systems[J]. Journal of Vibration and Acoustics, 1997, 119(1):9—20.

[22]凌复华. 非线性振动系统周期运动及其稳定性的数值研究[J]. 力学进展, 1986, 16(1):14—27.

Ling Fuhua. Numerical treatments of a periodic motion and its stability of nonlinear oscillation systems[J]. Advances in Mechanics, 1986, 16(1):14—27.

[23]Han S M, Benaroya H. Non-linear coupled transverse and axial vibration of a compliant structure, PART 1: Formulation and free vibration[J]. Journal of Sound and Vibration， 2000， 237(5):837—873.

[24]钟一鄂,何衍宗,王正，等. 转子动力学[M]. 北京：清华大学出版社，1986.

[25]Nayfeh A H. Introduction to Perturbation Techniques[M]. John Wiley & Sons， 2011.

[26]查金荣.非线性微分方程两点边值问题数值解法综述[J]. 化工冶金, 1983，(02): 81—91.

[27]刘恒, 陈丽. 周向均布拉杆柔性组合转子轴承系统的非线性动力特性[J]. 机械工程学报, 2010，(19): 53—62.

LIU Heng, CHEN Li. Nonlinear dynamic analysis of a flexible rod fastening rotor bearing system[J]. Journal of Mechanical Engineering, 2010(19): 53—62.

[28]宋学宾, 刘恒，易均，等. 推力轴承对柔性转子系统的非线性动力影响[J]. 西安交通大学学报, 2011，(09): 108—113.

SONG Xuebin, LIU Heng， YI Jun， et al. Nonlinear dynamic effect of thrust bearing on a flexible rotor system[J].Journal of Xi′an Jiaotong University， 2011，(09): 108—113.

[29]易均, 刘恒， 刘意，等. 接触界面对拉杆组合柔性转子轴承系统的非线性动力特性影响[J]. 振动与冲击, 2012，(17): 165—170，175.

YI Jun, LIU Heng， LIU Yi，et al. Effect of contact interface upon nonlinear dynamic properties of a flexible rod fastening rotor bearing system[J].Journal of Vibration and Shock， 2012,(17): 165—170，175.

[30]易均, 刘恒，刘意，等. 歪斜安装对组配轴承转子系统动力学特性影响[J]. 西安交通大学学报, 2014，(09): 107—111.

YI Jun, LIU Heng， LIU Yi， et al. Influence of installed outer race on nonlinear dynamic characteristics for matched bearings rotor system[J]. Journal of Xi′an Jiaotong University, 2014,(09): 107—111.

[31]李辉光, 刘恒, 虞烈, 周向拉杆转子系统非线性动力行为及稳定性[J]. 机械工程学报, 2011,(23): 82—91.

LI Huiguang, LIU Heng, YU Lie. Nonlinear dyanmic behaviors and stability of circumferential rod fastening rotor system[J]. Journal of Mechanical Engineering, 2011,(23): 82—91.

[32]周纪卿. 非线性振动[M]. 西安：西安交通大学出版社, 1998.

[33]Zou D, Rao Z, Ta N, Coupled longitudinal-transverse dynamics of a marine propulsion shafting under superharmonic resonances[J]. Journal of Sound and Vibration, 2015， 346(0): 248—264.

[34]R 克拉夫, J 彭. 结构动力学[M].北京: 高等教育出版社， 2006.

[35]周进雄, 诸德培, 高建平. 基于多重打靶技术的连续法求解非线性自治系统的周期解[J]. 机械强度, 1999, 21(02):20—22,27.

Zhou Jinxiong, Zhu Depei, Gao Jianping. Continuation method for the numerical solution of periodic motions of nonlinear autonomous systems by multiple shooting techniques[J].Journal of Mechanical Strength, 1999, 21(02):20—22,27.

Primary resonances of shafts with coupled longitudinal-transverse vibration by finite element and shooting methods

ZOUDong-lin1,2,LIULing1,2,RAOZhu-shi1,2,TANa1,2

(1.Insitute of Vibration, Shock and Noise, Shanghai Jiao Tong University, Shanghai 200240, China；2.State Key Laboratory of Mechanical System and Vibration, Shanghai Jiao Tong University, Shanghai 200240, China)

A coupled longitudinal-transverse nonlinear dynamic model of shafts is established by Hamilton's principle and finite element method with consideration of the Von Karman's nonlinear strain-displacement relationship. The nonlinear stiffness matrix is derived. Then the transverse primary resonances under excitation load are studied and the stabilities are analyzed by shooting method. The influence of the load, damping ration and slender ratio on the nonlinear effect is discussed . Results show that the lateral resonant frequency is larger than the linear natural frequency due to the nonlinear effects for hard springs. For some frequencies, there are multiple stable solutions in the amplitude-frequency curve and jump phenomena as well. The bigger the load, the smaller the damping ratio and the smaller the slender ratio is, the bigger the nonlinear effect is. The nonlinear effects could be suppressed and the stability could be improved by increasing the damping ratio. These analyses provide reference and guidance to the design of shafts.

nonlinear vibration； coupled longitudinal-transverse shafts; FEM; shooting method; primary resonance

2014-09-09；

2015-09-08

O322；TH113.1

A

1004-4523(2016)01-0087-09

10.16385/j.cnki.issn.1004-4523.2016.01.012

邹冬林(1987—),男,博士研究生。电话:18818214080; E-mail: zoudonglin.520@sjtu.edu.cn