砂土阻尼比确定方法对比分析

2022-02-28冯震郭涛宋东松

科学技术与工程 2022年5期

冯震，郭涛，宋东松

(1.河北大学建筑工程学院，保定 071002； 2.河北省土木工程监测与评估技术创新中心，保定 071002)

阻尼比主要反映土体动剪应力-动剪应变关系的滞后性特性，是土的基本动力特性参数，也是场地地震反应分析不可缺少的基础性资料。阻尼比自20世纪70年代Seed等[1]对无黏性土的研究时出现以来，已经有50多年的发展历史了，期间对砂土的研究较为充分，Amr等[2]对埃及钙质砂的动力特性进行了评价；Jafarian等[3]对各向同性及异性条件下的钙质-硅质砂的动力特性做了研究；Pradeep等[4]对印度北部砂土地震反应特性进行了研究；朱成浩等[5]对粉砂动本构模型做了研究；韩丽君等[6]对应力和应变控制下饱和砂土的循环扭剪特性做了研究。同时研究的土类也从无黏性土扩展到粉土[7]、黏性土[8]、海洋土[9]、冻土[10]、人工合成土等[11]。目前，中外对阻尼比的动力特性研究已经相对成熟，然而对阻尼比的确定方法却没有达成共识。

阻尼比确定方法大致可以分为两类：滞回圈法和滞后角法(时间相位差法)。其中，滞回圈法在中外应用最为广泛，阻尼比定义为一个周期内消耗应变能(滞回曲线的面积)与一个周期内储存的应变能的比值，目前对储存应变能的确定还不统一，陈伟等[12]、Das等[13]、李瑞山等[14]、Kokusho[15]、Kumar等[16]各自提出了不同的修正方法。滞后角法是一种传统方法，根据剪应力-剪应变时程曲线来确定阻尼比[17-18]。具体是根据剪应力、剪应变间的时间相位差来确定，该方法对试验数据的采样频率有较高的要求，数据点越多阻尼比的计算精度越高。

中外学者提出了多种确定方法来确定阻尼比，但是对于各种确定方法以及确定的结果之间的差异性尚不得知。因此，研究各种确定方法之间的差异性，以及确定合理的处理方法具有重要的研究价值。

为此，现以福建标准砂(粒径0.5～1.0 mm)为试验对象，采用动三轴试验，选用传统法、Das法、Kokusho法、Kumar法、互相关函数法为确定阻尼比的典型代表，将几种方法确定的结果进行对比，评价它们之间的差异性，给出使用建议，为工程应用中合理选用阻尼比确定方法提供重要参考。

1 阻尼比确定方法

目前中外学者大多基于滞回圈法确定阻尼比，具有代表性的阻尼比确定方法及特点如下。

(1)陈伟等[12]对传统使用等效椭圆计算一个周期内消耗的应变能进行了改进，提出了一种用多边形逼近滞回曲线计算滞回圈的面积(一个周期内消耗的应变能)，该方法可直接利用试验数据进行计算，算法可重复利用，使得阻尼比的计算工作得以简化，目前中外学者大多采用此法来计算滞回圈的面积。

(2)Das等[13]、李瑞山等[14]指出传统方法计算阻尼比时，在计算最大弹性应变能时只利用了正向加卸载半周的信息，对于理想对称的滞回圈，这种做法较为理想，但在剪应变较大时，正向半周和反向半周出现不对称情况，这种做法将会导致阻尼比结果偏差较大。对此，他们对传统的方法进行了修正，取滞回曲线顶点连线与剪应变坐标轴围成的两个三角形面积(第一象限、第三象限)的均值为一个周期内储存的应变能。

(3)Kokusho等[15]对传统的方法进行了改进，考虑了剪应力、剪应变在大应变下滞回曲线正负半轴的不对称性，对一个循环周期内存储的应变能进行了修正，取滞回曲线顶点的连线，分别作纵横坐标轴的垂线并交于一点，取围成三角形面积的1/4为一个周期内存储的应变能。

(4)Kumar等[16]对Kokusho法进行了改进，将滞回曲线顶点的连线修正为分别于原点连线，取围成的多边形的面积的1/4为一个周期内储存的应变能。

同时，也有少数学者基于信号处理方法给出了阻尼比的确定方法，例如，罗飞等[17]根据冻黏土的剪应力-剪应变滞回曲线特性，提出了确定冻黏土阻

尼比的互相关函数法；梁珂等[18]对相关函数法进行了拓展，根据相关函数反映两个波形在不同时刻的相似程度的物理意义，采用互相关函数分析应变滞后于应力时程波形的相位差，进而计算阻尼比。

为充分认识各种阻尼比确定方法之间的差异，以及确定结果之间的差异性，现选用以下几种确定方法为典型代表。

1.1 传统法

美国土工试验标准D3999[19]对阻尼比的定义为

(1)

式(1)中：λ为阻尼比；WD为一个循环周期内消耗的应变能；WS为一个循环周期内存储的应变能。如图1所示，滞回圈的面积表示WD，阴影部分的面积表示WS。

对于一个循环周期内消耗的应变能WD的计算，陈伟等[12]提出了一种可使用原始试验数据多边形逼近剪应力-剪应变滞回曲线的方法，直接进行滞回圈面积的计算，一个循环周期内消耗的应变能计算公式为

(2)

式(2)中：τi为一个循环周期内记录的剪应力；γi为一个循环周期内记录的剪应变；n为一个循环周期内记录的剪应力-剪应变点总数。

τd为动剪应力幅值；γ为剪应变幅值；点a、c分别为滞回圈的两个顶点坐标;点d、b分别为正最大剪应变、负最小剪应变图1 传统法Fig.1 Traditional method

1.2 Das法

对一个周期内存储的应变能进行了修正，如图2所示，取阴影三角形面积之和的均值为一个周期内储存的应变能，则阻尼比计算公式为

(3)

式(3)中：WS1、WS2为一个循环周期内存储的弹性应变能分量。

图2 Das法Fig.2 Das method

1.3 Kokusho法

对一个周期内存储的应变能进行了修正，如图3所示，取阴影三角形面积的1/4为一个周期内储存的应变能，则阻尼比计算公式为

(4)

式(4)中：WS1为Δabc的面积。

图3 Kokusho法Fig.3 Kokusho method

1.4 Kumar法

Kumar等对Kokusho法进行修正，如图4所示，取阴影多边形面积的1/4为一个周期内储存的应变

Gmax为最大动剪切模量，MPa；Gsec1为加荷部分的动剪切模量，即滞回曲线正半轴顶点与原点的斜率，MPa；Gsec2为卸荷部分的动剪切模量，图中为滞回曲线负半轴顶点与原点的斜率，MPa；O点至a点为正向加载阶段，a点至b点为正向卸载阶段，b点至e点为反向加载阶段，e点至f点为反向卸载阶段图4 Kumar法Fig.4 Kumar method

能，则阻尼比计算公式为

(5)

式(5)中：WS3为一个循环周期内存储的弹性应变能分量。

1.5 互相关函数法

阻尼比的另一种表达形式是根据耗损系数η来定义的[20]，其表达式为

(6)

(7)

式中：φ为动剪应力、剪应变时程曲线的相位差。

因此只要确定了动剪应力、应变时程曲线的相位差就可以准确的得到阻尼比，梁珂等[18]根据互相关函数的定义，对试验数据按式(8)处理，得到动剪应力、剪应变时程曲线最大相关性时对应的时间t0(图5)为

i=0，1，2，…，NN0-i

(8)

式(8)中：Rτγ(iΔt)为第iΔt时刻实测剪应力、剪应变波形的互相关函数值;N0为每周期记录的试验点数;N为循环次数;τk、γk+i分别为第kΔt时刻的剪应力试验值、第(k+i)Δt时刻的剪应变试验值。

根据互相关函数最大值对应的时间t0计算应力、应变波形的相位差，将式(9)代入式(7)中得到阻尼比计算公式为

φ=ωt0

(9)

(10)

式中：ω为加载频率。

图5 互相关函数法原理Fig.5 Cross-correlation function method principle

2 室内试验

2.1 试验设备

试验设备采用西安康拓力公司生产的新型电机伺服控制动三轴仪(图6)，实验所采用动三轴系统主要性能参数如表1所示。

①为微机；②为数据采集仪；③为伺服控制器；④为压力室；⑤为力控制器；⑥为试样；⑦为反压控制器；⑧为围压控制器；⑨为二氧化碳瓶图6 KTL动三轴仪Fig.6 KTL dynamic triaxial apparatus

表1 KTL动三轴系统主要性能参数Table 1 KTL dynamic triaxial system performance parameters

2.2 试样

为验证几种方法确定阻尼比的差异，采用粒径为0.5～1.0 mm的福建标准砂作为研究材料(图7)，以验证几种方法确定的阻尼比的差异性。动三轴仪试验参照《土工试验方法标准》[21](GB/T 50123—2019)进行操作，所制备试样直径为50 mm，高度为100 mm。福建标准砂的基本物性指标如表2所示。

2.3 试验方案

试验采用应力控制、多级加载方式，应力由小到大逐级加载。加载波形采用正弦波，加载频率为1 Hz。采用相对密实度Dr为30%、60%、80%的土样分别进行试验。

砂样制备直接在动三轴仪上完成，采用干砂装样法装样，共分5层均匀制样，严格控制每层厚度为20 mm；试样饱和采用先通30 min二氧化碳置换试样孔隙中的空气，然后通入无气水进行水头饱和，水头饱和完成后采用分级反压饱和方式进行土体饱和，当试样孔压参数B达到0.95以上，认为试样饱和度达到要求。

采用等压固结方式固结，试样固结压力分别为100、300和500 kPa，具体试验方案如表3所示。

图7 福建标准砂(粒径0.5～1.0 mm)颗粒电镜扫描Fig.7 Scanning electron microscope of Fujian standard sand (particle size 0.5～1.0 mm)

表2 试样基本物性性质Table 2 Basic physical properties of samples

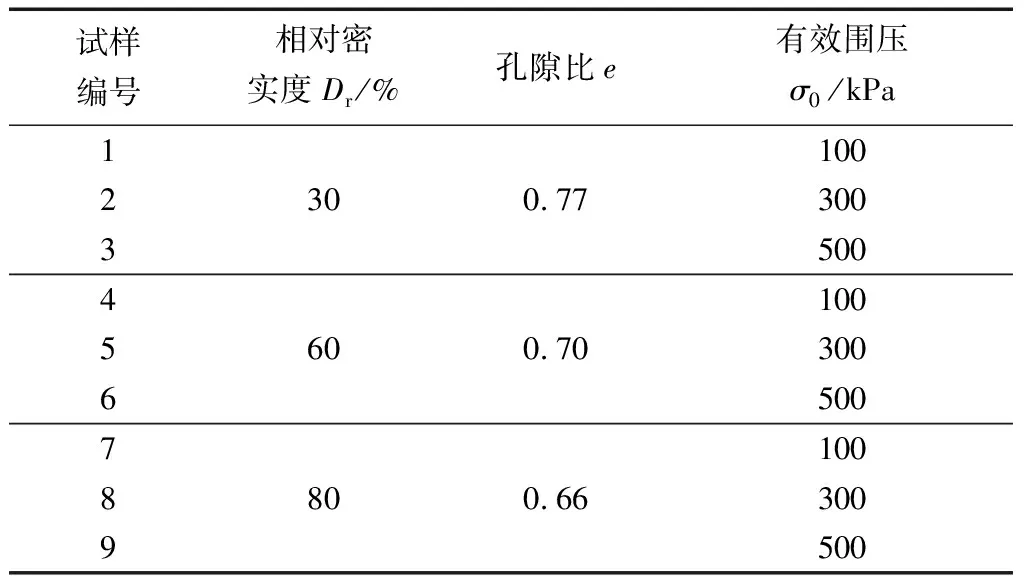
表3 试验方案Table 3 Test plan

3 阻尼比计算结果

3.1 5种方法计算结果对比

图8～图10给出了传统法、Das法、Kokusho法、Kumar法和互相关函数法5种方法确定的阻尼比。

图8 Dr=30%时不同围压下阻尼比-剪应变曲线Fig.8 Damping ratio-shear strain curve of different confining pressures when Dr=30%

图9 Dr=60%时不同围压下阻尼比-剪应变曲线Fig.9 Damping ratio-shear strain curve of different confining pressures when Dr=60%

从图8～图10可以看出：剪应变小于10-3时，传统法、Das法、Kokusho法、Kumar法这4种方法确定的阻尼比基本一致，互相关函数法确定的阻尼比比其他4种方法较大，但随着有效围压的增大互相关函数法确定的阻尼比与另外4种方法确定的阻尼比的差值在逐渐减小；剪应变大于10-3时，随着剪应变的增大，5种方法确定的阻尼比差值在逐渐增大；互相关函数法确定的阻尼比最大，其他4种方法确定的阻尼比由大到小依次是Kumar法、Das法、Kokusho法、传统法。有效围压较低时，Das法在剪应变大于3×10-3时确定的阻尼比比Kokusho法小，随有效围压增大，两者确定的阻尼比逐渐趋于一致。

3.2 差异性

为了更直观地评价各种方法的优劣，采用相对误差作为评价指标，计算公式为

(11)

式(11)中：δ为相对误差；λ为阻尼比；λavg为平均阻尼比。

图11～图13给出了传统法、Das法、Kokusho法、Kumar法和互相关函数法5种方法确定的阻尼比的相对误差。

图10 Dr=80%时不同围压下阻尼比-剪应变曲线Fig.10 Damping ratio-shear strain curve of different confining pressures when Dr=80%

图11 Dr=30%时不同围压下相对误差-剪应变曲线Fig.11 Relative error-shear strain curve of different confining pressures when Dr=30%

从图11～图13可以看出：当剪应变小于10-3时，随着剪应变的增大5种方法确定的阻尼比相对误差在迅速减小，当剪应变大于10-3时，减小趋势缓慢并趋于稳定。

互相关函数法确定的阻尼比远大于平均阻尼比，并且，最大相对误差基本都出现在第一级荷载下，随有效围压的增大而逐渐增大；Kumar法确定的阻尼比最接近平均阻尼比，在剪应变小于10-3时，低于平均阻尼比，剪应变大于10-3时，高于平均阻尼比；Das法和Kokusho法确定的阻尼比基本一致，低于平均阻尼比；传统法确定的阻尼比远低于平均阻尼比。

3.3 分析讨论

分析前述试验结果，5种阻尼比确定方法产生差异性的原因是：阻尼比是由每周的能量耗损与储存的弹性应变能之比来确定的，滞回圈法确定的每周能量耗损都为剪应力-应变滞回曲线围成的面积，但是对存储的弹性应变能确定方法不同。传统法计算的储存应变能为第一象限三角形的面积，未考虑在大剪应变下滞回曲线不对称的情况，计算结果最大，Das法、Kokusho法考虑了大剪应变下滞回曲线的不对称性，计算的储存应变能比传统法小，而Kumar法是对Kokusho法进行了修正，计算的存储应变能比Kokusho法小；滞后角法则是根据剪应力应变时程曲线的时间相位差来确定阻尼比。

在实际工程应用时，如果采用应力控制加载，确定阻尼比采用Kumar法比较可靠，主要由于5种确定阻尼比的方法中，Kumar法确定的阻尼比最接近平均阻尼比。