基于等额本金按揭贷款的脉冲增加还款模型
2016-09-09茹永梅三明职业技术学院人文社会科学系福建三明365000
茹永梅(三明职业技术学院 人文社会科学系,福建 三明 365000)
基于等额本金按揭贷款的脉冲增加还款模型
茹永梅
(三明职业技术学院 人文社会科学系,福建 三明 365000)
为指导人们合理制定按揭贷款计划,利用一阶线性差分方程建立了基于等额本金按揭贷款的每隔半年还款一次的数学模型,并通过应用实例说明其在经济生活中的应用.
按揭贷款;等额本金还款模型;脉冲增加还款模型;数学模型
1 问题的提出
近年来,随着我国商业住房产业化制度的推进、按揭政策的放宽及居民收入水平的提高,商业住房日益成为我国居民新的消费热点.房改政策、城镇化趋势和居民财富增加后,对住房需求的提升推动了居民购房需求的增长.居民购房前,只有根据自己的收入理性地确定贷款额,了解贷款后每期的欠款额、剩下期数、总期数、每期的还款额和总还款额,及时调整投资策略,才不会在购房中盲目贷款或造成过大压力.目前,银行按揭贷款已成为人们普遍采用的一种购房方式.叶其孝依据中国人民银行的规定建立了等额本息、等额本金、等本等息等额三种按揭贷款模型[1].钱晓莉建立了每隔6个月每月增加(或减少)还款K元的数学模型[2].文献[1]和文献[2]为人们在购房时如何理性选择适合自己的贷款方式提供了一定的指导.
由于商业贷款的利率一般要比住房公积金贷款的利率高,居民在购房时一般首选公积金按揭贷款.商业贷款中,职工每半年可将积攒下来的余款用于偿还各种贷款.公积金按揭贷款中,职工每半年提取一次住房公积金用于还贷,这种还款方式称为脉冲增加还款方式[3-4].王积建建立了基于等额本息按揭贷款的脉冲增加还款模型,但没有考虑等额本金的情况[4].实际生活中,居民购房时存在以等额本金为基础进行按揭贷款的情况.本文对文献[4]的模型加以改进,利用文献[5]中的差分方程法建立以等额本金按揭贷款为基础的脉冲增加还款模型,完善脉冲增加还款模型的体系,使其更好地服务于居民购房贷款还款的实际需求.
2 符号说明与模型假设
2.1符号说明
A0为贷款额(元),r为月利率,N为原计划还款期数,n为还款月数,An表示第n个月后的欠款额(n∈Z,1≤n≤N,元),Hn为每月还款额(元),Ln为每月利息(元),a为每隔6个月一次性增加的还款额(元), A6m+p为第m次脉冲增加还贷后的第p个月还款后的欠款额(m=0,1,2,3,…,M;p∈Z,0 2.2模型假设 为简化问题并建立适合一定条件下的脉冲还款模型,提出以下模型假设: (1)银行利率在居民贷款期内不受国家政策、通货膨胀、经济危机等因素的影响,始终保持不变; (2)居民按月计算利率和贷款期限; (3)居民在每月最后一天还款; (4)货币价值在居民贷款期限内不升值、不贬值; (5)每半年的一次性增加还款时间发生在该半年的最后一天; 3.1等额本金还款模型 已知居民购房时的本金为A0,根据银行计利方式可建立等额本金还款模型为: 按照这种方法得到的该居民第n个月后的欠款额为: 第n个月的还款额为: 每月还款额是递减的,递减额为: 总期数为: 贷款额为: 月利率r为: 总还款额为: 第n个月的利息为: 总利息为: 3.2等额本金-脉冲增加还款模型 根据模型假设及3.1给出的等额本金还款模型可建立等额本金-脉冲增加还款模型为: 当a=0时,(12)式就成为(2)式,所以等额本金还款模型可看作等额本金-脉冲增加还款模型的特殊情况. 其中Nm为非负有理数,并规定当m=0时,N0=N.总期数为: 3.2.3脉冲增加还款额和脉冲次数.将A6M+NM=0代入(1 2)式得,每半年的增加还款额为: 脉冲次数为: 当NM=0时,脉冲次数为: 3.2.4贷款额.贷款额为: 其中M依赖于A0.如果A0未知,那么M就无法求出,因而A0就无法求出. 采用迭代思想设计一个近似算法,步骤如下: (1)给定N,取n=1,给定Hn,由(6)式可得不脉冲情况下的贷款额A0; (2)给定a,由(17)式可得脉冲情况下的M; 3.2.5还款额和总还款额.如果第n期不是最后一期,则第n期的还款额为: 规定当m=0, p=0时,H0=0. 如果第n期是最后一期,则第n期的还款额分类讨论如下: 则 正常月比脉冲月的递减额为: 正常月的递减额为: 总还款额分类讨论如下: 3.2.6利息和总利息.如果第n期不是最后一期,则第n期的利息为: 规定:当m=0, p=0时,L0=0. 如果第n期是最后一期,则第n期的利息分类讨论如下: 总利息分类讨论如下: 规定:当m=0时,r0=r. 王积建以"某对夫妇计划公积金贷款30万元,月利率为0.003 225,月还款能力为2 000元,10年还清,每半年可提取公积金15 500元还款"为例,研究并得到一些结论[4].本文根据所建模型,在文献[4]已有结论的基础上,继续研究以下问题: (1)如果不提取公积金还款,第7个月的还款额和第7个月的利息各多少元? (2)如果提取公积金还款,第7个月的还款额和第7个月的利息各多少元? (3)如果提取公积金还款,那么总还款期数是多少? (4)提取公积金还款比不提取公积金还款减少利息支出多少元? (5)如果要求4年还清,那么每半年增加还款额必须提高至多少元? (6)如果他们想尽可能多贷一些款,于是将每月积攒的2 000元和公积金15 500元一起全部用于还贷, 5年内还清,那么能够贷款多少元? 解(1)此时,A0=300 000,r=0.003 225,a=0, N= 120.当m=1, p=1时,代入(19)式的第2个公式得第7个月还款额为H7=3 419.13元.代入(28)式的第2个公式得第7个月利息为L7=919.13元. (2)在(1)的基础上,a=15 500,代入(19)式的第2个公式得第7个月还款额为H7=3 369.14元.代入(28)式的第2个公式得第7个月利息为L7=869.14元.这样比(原来不脉冲还款情况下)919.13元减少利息49.99元. (3)确定m, p,使得A6m+p≤0,且A6m+p-1>0.根据(12)式,通过尝试,当m=10, p=0时,A6m+p= -5 000≤0,而当m=9, p=5时,A6m+p=13 000>0,所以在第60个月可全部还清贷款,即只需要5年即可还清贷款. (4)在不提取公积金还款的情况下,由(10)式可知,总利息为58 533.75元;在提取公积金还款的情况下,由(32)式可知,总利息为30 282.75元.这样可减少利息支出28 251元. (5)M=8, NM=0,由(15)式得a=22 500,即每半年增加还款额必须提高至22 500元.也就是说,他们除了提取15 500元公积金外,还需要额外拿出7 000元用于还贷. (6)采用A0的迭代算法.取n=1,给定Hn=5 000,给定a=15 500+2 000X6=27 500,通过迭代,当N=139时,得A0=479 881.24,M=9.95<2X5.所以大约可贷款48万元,比原来多贷款18万元. 等额本金-脉冲增加还款模型可帮助居民根据自己的收入合理确定贷款额,并了解贷款后每期的欠款额、剩下期数、每期还款额、脉冲增加还款额等,为居民及时调整还贷方式提供依据,也使得银行贷款的透明度得以提升,从而实现银行与居民购房贷款的双赢. [1]叶其孝.大学生数学建模竞赛辅导教材(五)[M].长沙:湖南教育出版社,2008:52-59. [2]钱晓莉.按揭贷款模型的研究[J].数学的实践与认识,2002,32(5):733-737. [3]2016最新住房公积金管理条例全文[EB/OL].(2015-11-20)[2015-12-20].http://www.liuxiaoer.com/ct/1991.html. [4]王积建.基于等额本息按揭贷款的脉冲增加还款模型[J].数学的实践与认识,2011,41(3):67-71. [5]韩中庚.数学建模方法及其应用[M].北京:高等教育出版社,2005:55-68. [责任编辑:王积建] Analysis Based on Pulse Increased Repayment Model of Average Capital Mortgage Loan RU Yongmei In order to help people to make rational mortgage loan plan, first order linear difference equation is applied to forming the mathematics model based on average capital mortgage loan to make the repayment once every half a year. Cases will be analyzed to clarify how to employ it in economic life. Mortgage loan; Repayment model of average capital; Pulse increased repayment model; Mathematics model F832.4;F244.0 A 1671-4326(2016)02-0055-05 10.13669/j.cnki.33-1276/z.2016.038 2016-01-06 茹永梅(1979-),女,陕西宝鸡人,三明职业技术学院人文社会科学系讲师,硕士.3 模型的建立与求解
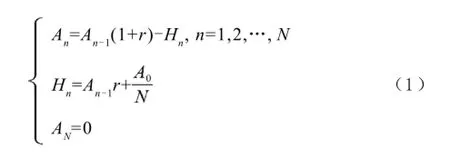






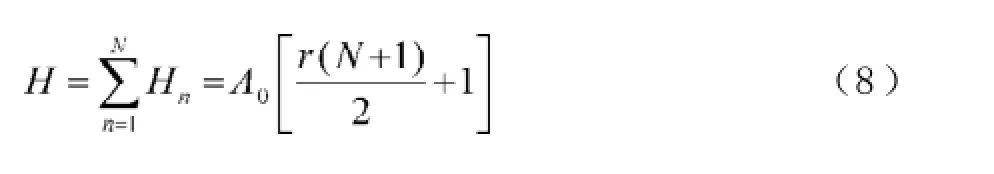
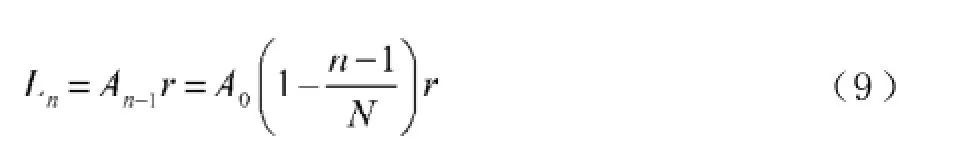

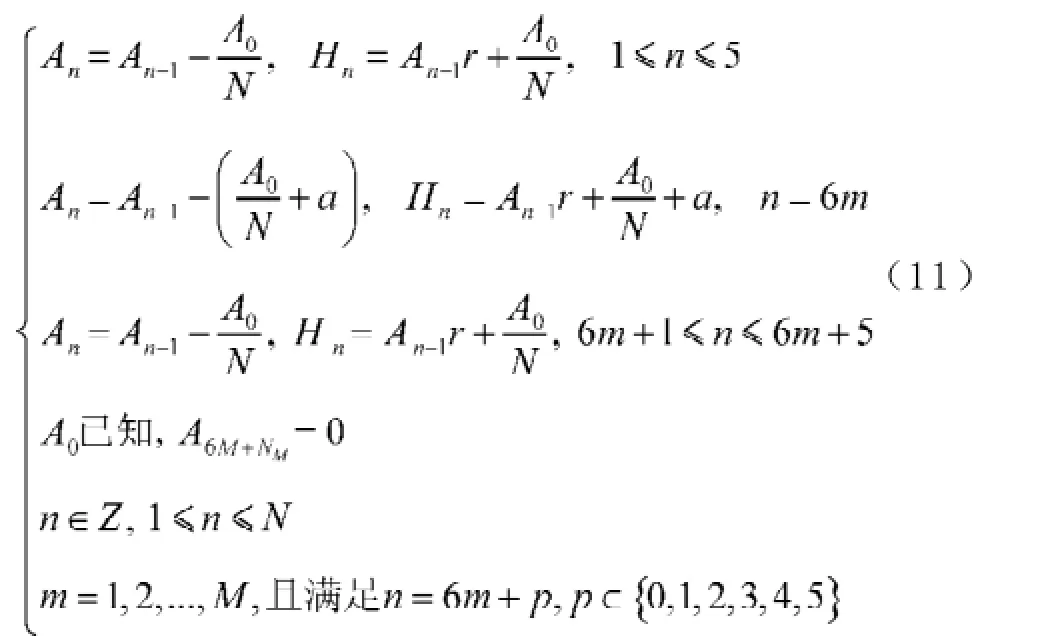
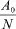

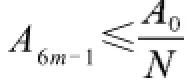
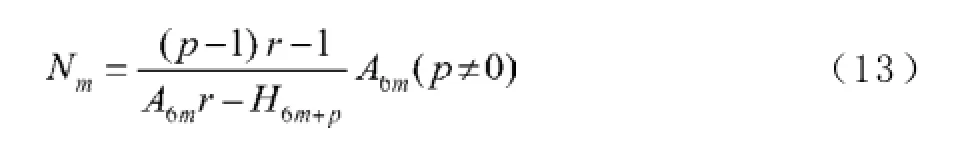
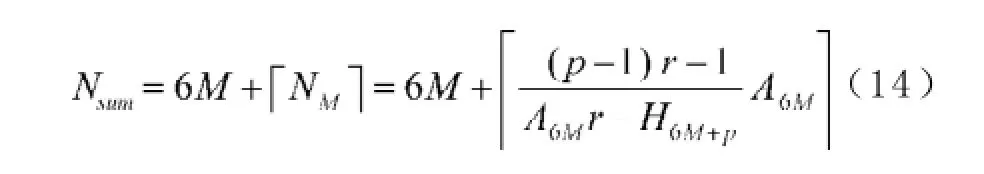




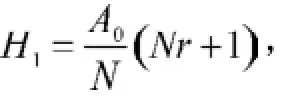
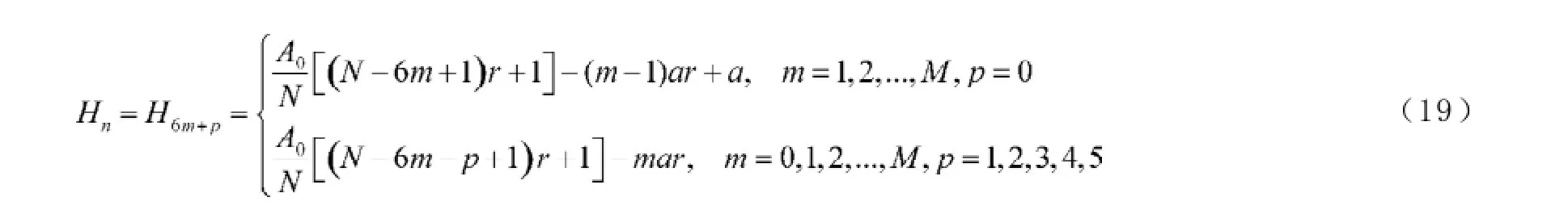



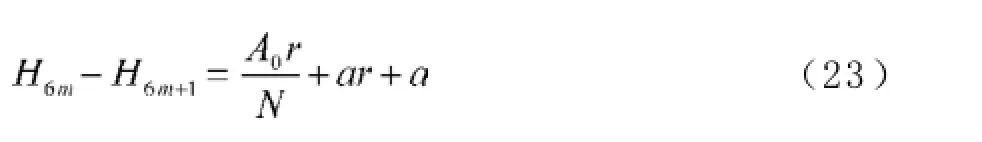

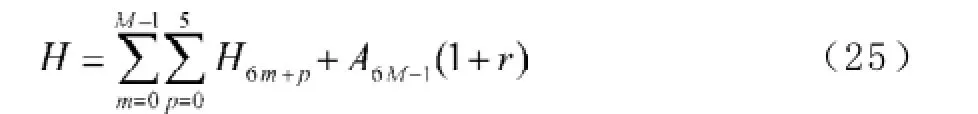
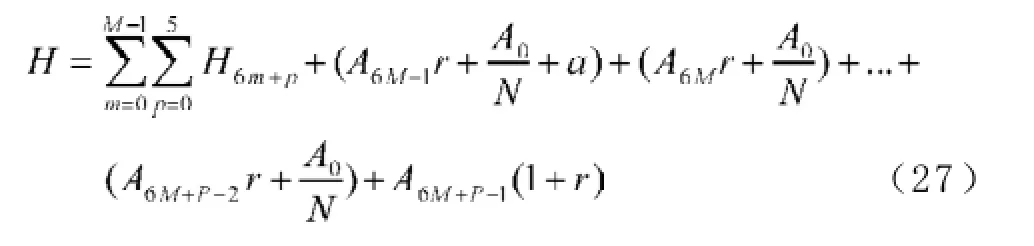
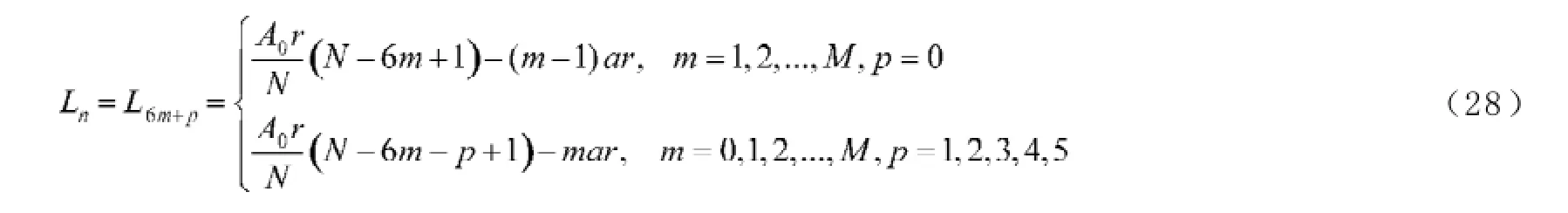



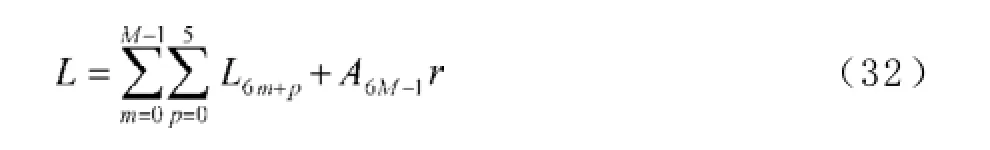
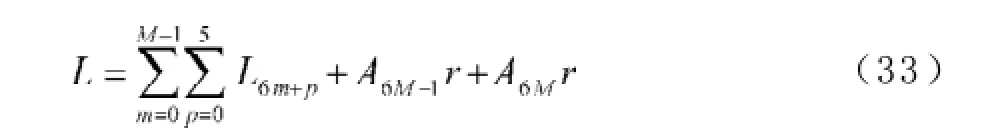
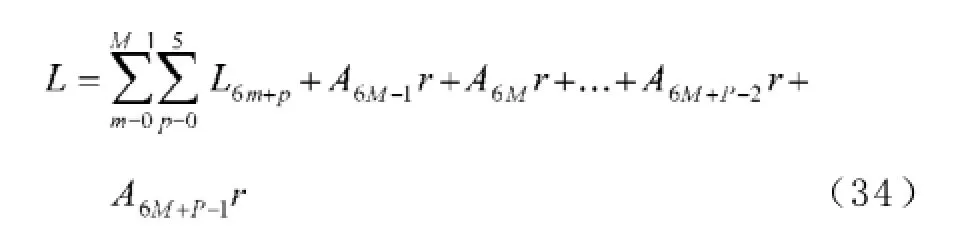

4 应用实例
5 结束语
(Department of Humanities and Social Science, Sanming Vocational Technical College, Sanming, 365000, China)
