n！的质因数分解的新发现

赵云平（滇西科技师范学院数理系，云南 临沧 677099）

n！的质因数分解的新发现

赵云平
（滇西科技师范学院数理系，云南 临沧 677099）

n！的质因数分解是高斯函数（或取整函数）在初等数论中的一个应用，针对n！的质因数分解作了初步探讨，通过实例给出n！的质因数分解中质因数指数的一种简洁求法。

n！；质因数；指数；分解

0　引言

把一个大于1的整数N分解成质因数的乘积，要找出它所有的质因数，首先找出的质数，再判断这些质数是不是N的质因数，最后把它写成质因数乘积的形式，这个工作量是非常大的。但是对于一类特殊的问题来说，把它分解成质因数的乘积会比较容易一些，是什么样的数呢？就是这个阶乘。我们要讨论阶乘的分解，就要用到函数［X］，下面我们先来认识一些相关概念及结论。

1　预备知识［1-5］

定义1：在大于1的整数中，若某数p除了1和它本身以外没有其它的因数，这种整数叫做质数，也称为素数。否则称为合数。

定义2：把一个合数分解成若干个质数乘积的形式，其中每个质数都是这个合数的因数，叫做这个合数的分解质因数。分解质因数只针对合数。

定义3：若X∈R，函数［X］的值是不超过X的最大整数，我们把［X］叫做方括号函数或高斯函数，它是X的整数部分。

定理1：如果a是大于1的整数，则a的除1以外最小的正因数p一定是质数，并且当a为合数，。

证明：因为a是大于1的整数，所以大于1的正因数一定存在，a本身就是一个。下面证明第1个结论：a的除1以外最小的正因数p一定是质数，我们用反证法。

若p不是质数，p就是合数，则p=p1p2，2≤p1，p2≤p，1＜p1＜p，且p1p，又因为p是a的因数，有p a，所以p1a，又p是大于1的，与p是a的大于1的最小正因数矛盾，所以p一定是质数。

因为a是合数，设a=a1p，且a1＜1，p≤a1，p2≤ a1p=a，。

定理2（算术基本定理）：任一大于1的整数a能表示成质数的乘积，即a＜1，则a=p1，p2，…，pn，p1≤p2≤…≤pn，其中p1是质数，p1为a的质因数。

［注意］

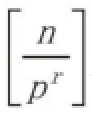
推论1：任一大于1的整数a能够唯一地写成a=p1a1，p2a2，…，pkak（称为a的标准分解式），ai＞0，i= 1，2，…，k。其中pi＜pj（i＜j）。

［注意］

n！=1×2×…×n，故小于等于n的质因数在n！中一定出现。

2　n！的质因数分解的步骤

第一，先找≤n的所有质数，即先写出1到n的所有正整数，找到的质数，在1到n的数中首先划掉1，再划掉的这些质数的倍数，剩下的就是n以内的质数；

第二，应用定理3计算各质因数的指数；

第三，若质因数pi对应的指数为ai，则

n！=p1a1，p2a2，…，prar

例如算20！的质因数分解。

方法一：

分析：因为20！=1×2×3×4×5×6×7×8×9×10×11× 12×13×14×15×16×17×18×19×20，故不超过20的质数在20！的质因数分解式中一定出现。1既不是质数也不是合数，去掉1，质数2、3、5、7、11、13、17、19保留，接下来把剩余合数4、6、8、9、10、12、14、15、16、18、20用质因数分解的常规方法——短除法进行分解，就是先用一个合数的最小质因数去除这个合数，得出的数若是一个质数，就把这个合数写成质因数相乘的形式；剩余若仍然是一个合数，就继续按原来的方法分解，直至最后是一个质数，短除法就结束。如，合数4，它的最小质数是2，4=2×2；合数6，它的最小质数是2，6=2×3；合数8，它的最小质数是2，8=2×4，4再可以分解，8=2×2×2；合数9，它的最小质数是3，9=3×3；类似的10=2×5，12=2×2×3，14=2×7，15=3×5，16=2×2×2×2，18=2×3×3，20=2×2× 5。

综上，20！=2×3×2×2×5×2×3×7×2×2×2×3×3×2× 5×11×2×2×3×13×2×7×3×5×2×2×2×2×17×2×3×3× 19×2×2×5

即

20！=218×38×54×72×11×13×17×19

从计算上看，方法一比较繁琐，当合数增大时计算量随之增大，故此方法只适用于不太大的合数，特别是对于n！这类特殊的数，不建议使用此方法。

方法二：

分析：将不超过20的正整数排列如下

12345678910

11 12 13 14 15 16 17 18 19 20

先找≤20的质数，即先找≤＜5的质数，有2和3，首先把1划去，然后从1至20的数中划去2和3的倍数，剩下的就是20以内的质数：

故≤20的质数有2、3、5、7、11、13、17、19，下面分别计算2、3、5、7、11、13、17、19的指数。

2的指数

3的指数

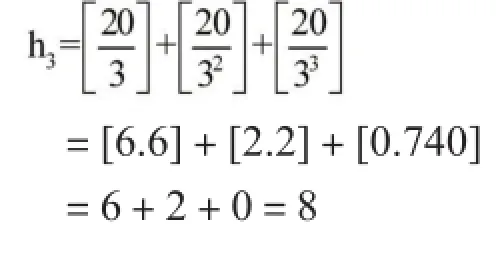
5的指数

7的指数

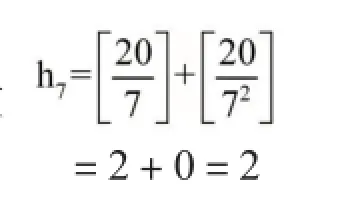
11的指数

13的指数

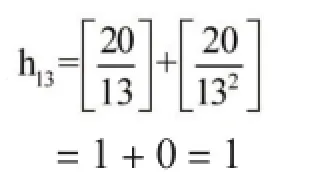
17的指数

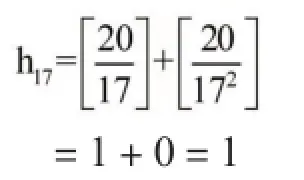
19的指数

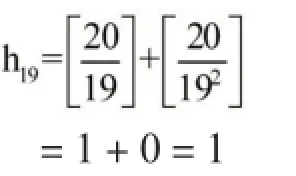
所以20！=218×38×54×72×11×13×17×19

从指数计算的过程中发现∶，依此类推，可以推广到有限个的情形。

则上述例题中指数的求法如下：

5的指数

这种新方法的优点在于不需要计算pr，只需在上一结果的基础上进行计算，特别对于p和r太大时，此方法可大大减少计算量；缺点在于，由于下一步的操作是在前一步的基础上进行，一旦前一步发生错误，就会出现连带作用，以致后面的结果也是错误的，所以希望大家用此方法时确保每一步准确无误，避免计算的损失。

总之，方法二较方法一而言，方法更简捷直接，不需要重复计算，对质因数指数的计算一步到位，方法二更适用于n！的质因数分解。

3　结语

质因数分解包含了对质因数的认识及对因数分解的掌握两个基本内容，文章虽然重点讨论n！的质因数分解，但是对于任何大于1的整数N的质因数分解也是类似的，不同的是，不用找出≤N的所有质数，只需筛选出的质数之后，判断这些质数是不是N的因数，更多相关的问题有待进一步探讨。

［1］潘承洞，潘承彪.初等数论［M］.北京大学出版社，2002:48-60.

［2］闵嗣鹤，严士健.初等数论［M］.3版.北京:高等教育出版社，2003:14-23.

［3］课程教材研究所.初等数论［M］.北京:人民教育出版社，2006:50-61.

［4］胡典顺，徐汉文.初等数论［M］.北京：科学出版社，2010:2-25.

［5］边红平.初等数论［M］.杭州：浙江大学出版社，2007:10-13.

ANew Discovery of Prime Factorizations of n！

ZHAO Yun-ping
（DepartmentofMathematics，DianxiScienceandTechnologyNormalUniversity，Lincang，Yunnan677099，China）

The prime factorizations of n！is an application of Gaussian function（or rounding function）［x］in elementary number theory.In view of the n！，the paper examines a preliminary discussion of the prime factors decomposition and put forward a simplified solution of prime factors index in the decomposition of prime factor of n！through specific examples.

n！；Prime Factors；Index；Decomposition

O156.2

A

1673-1891（2016）02-0021-03

10.16104/j.issn.1673-1891.2016.02.006

2016-03-24

赵云平（1982—），女，云南临沧人，硕士，讲师，研究方向:基础数学数论应用，运筹学线性规划，数值代数。