一阶常微分方程的奇解和包络的研究

徐丽君，廖永志（攀枝花学院 数学与计算机学院，四川 攀枝花 617000）

一阶常微分方程的奇解和包络的研究

徐丽君，廖永志
（攀枝花学院 数学与计算机学院，四川 攀枝花 617000）

微分方程F（x，y，y'）=0的奇解与包络等概念比较抽象，关系复杂，难以理解。利用包络和奇解的定义及有关定理，通过具体实例，用不同的方法研究方程F（x，y，y'）=0的奇解与包络，研究求曲线的奇解与包络的方法，讨论解的唯一性是如何被破坏的。

常微分方程，奇解，包络，通解

0　引言

常微分方程在很多学科领域内有着重要的应用，自动控制、各种电子学装置的设计、弹道的计算、飞机和导弹飞行的稳定性的研究、化学反应过程稳定性的研究等。这些问题都可以化为求常微分方程的解，或者化为研究解的性质的问题。常微分方程理论的应用已经渗透到经济、生物、工程各领域，关于方程解的存在性，解的唯一性被破坏的奇解和包络，初学者容易把这两个概念混淆。本文将以实例为主，重点分析这两个概念的内涵及其相互关系，希望能够降低教学难度，读者学习的难度。

1　奇解和包络的定义和定理

下面给出一阶常微分方程奇解和包络的定义，以及显示他们之间的关系定理，这是后面部分必须用的。定义1［1］：设Γ：y=φ（x）（x∈J）是一阶微分方程的一特解。如果对，在Q点的任何领域内方程（1.1）有一个不同于Γ的解在Q点与Γ相切，即解的唯一性被破坏，则称Γ是微分方程（1.1）的奇解。

定义2［1］：设在曲线族

Γ是平面上一条连续可微的曲线，如果对于任一点M∈Γ，都有一条曲线族（2）中的某一条曲线K （C*）通过M点并在该点与Γ相切，而且K（C*）在M点的某一领域内不同于Γ，则称曲线Γ为曲线族（2）的一支包络。

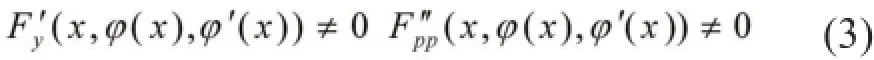
对x∈J成立，则y=φ（x）是微分方程（1）的奇解。

定理2［1］：设微分方程F（x，y，y'）=0有通积分U （x，y，y'）=0，又设（积分）曲线族有包络为Γ：y=φ （x）（x∈J），则包络y=φ（x）（x∈J）是微分方程（1）的奇解。

定理3［1］：设Γ是曲线族（2）的一支包络，则它满足如下的C-判别式或消去C，得到与之等价关系式：Ω（x，y）=0。

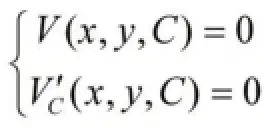
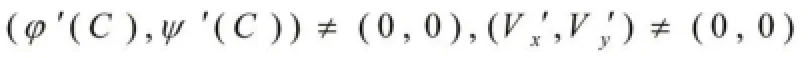
2　两个概念及其关系

由奇解与包络的定义显然可以知道，微分方程的积分曲线族（即通积分所对应的曲线族）的包络，如果存在，则由定理2知必定是方程的奇解，但奇解不一定是包络［2］。

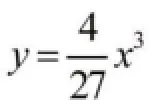
3　求奇解的方法

（1）它首先是方程的解；（2）其上点的唯一性被破坏［3］。

3.1定义法

利用Lipschitz条件检验解的存在与唯一性是比较费事的。然而，我们加强条件，即如果函数f（x，y）在闭矩形域R上关于y的偏导数fy'（x，y）存在并有界，则Lipschit条件同样成立，由此可以检验解的存在与唯一性。相反，找出方程不满足唯一条件的点的集合H（），只需fy（x，y）无界，也就是求使fy（x，y）为正负无穷的函数y=φ（x）（要求f（x，y）连续），再验证它是否是奇解或者是否包含有奇解即可［3］。

例2：判断下列方程是否存在奇解？

3.2拾遗法

指在求方程解的过程中，两边约去的相同因式或者求解变形过程作分母的式子，容易被遗漏［4］。如果令其为零，所得到的结果可能是奇解。

方程的通解是y=sin（x+C）。

此外还有y=±1也是方程的解，显然解y=1 和y=-1所对应的积分曲线上每一点，解的唯一性均被破坏。所以y=±1是原方程的奇解。

3.3p-判别法

（2）把p-判别曲线Φ（x，y）=0代入方程F（x，y，y'）=0，验证是否为方程的解。

（3）若是方程的解，则据定理3验证该分支是不是方程的奇解［1］。

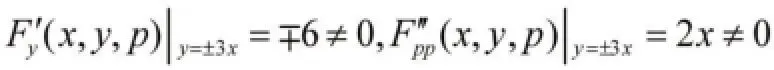
所以y=±3x是原微分方程的奇解。

3.4C-判别法

设微分方程F（x，y，y'）=0的通积分V（x，y，C）=0。

（2）把C-判别曲线代入方程F（x，y，y'）=0，验证是否为方程的解。

（3）若是方程的解，则据定理3与定理4验证是不是方程的包络。如果是，则一定是奇解［1］。

解：用参数法求微分方程的解。

对Λ1而言，因为，所以Λ1是通解的包络。

对Λ2而言，因为，所以Λ2不是通解的包络。

4　求包络的一般方法

4.1定义法

利用定义2对某些微分方程，求其积分曲线族的包络。

两边对x求导：

4.2C-判别法

设V（x，y，C）=0是微分方程F（x，y，y'）=0的通积分。

（2）用定理3与定理4验证该分支是不是方程的包络。

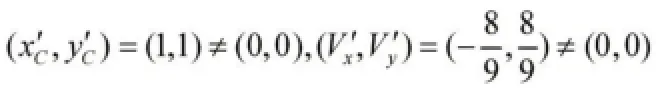
5　结语

微分方程F（x，y，y'）=0的奇解（若存在的话）是微分方程的通解的包络，反之，微分方程F（x，y，y'）=0的通解的包络（如果它存在的话）一定是奇解，因此为了求微分方程的奇解，可以先求出它的通解，然后再求通解的包络。

［1］丁同仁，李承治.常微分方程教程［M］.北京.高等教育出版社，1991.

［2］王高雄，周之铭，朱恩铭，等.常微分方程［M］.北京.高等教育出版社，2001.

［3］东北师范大学微分方程教研室.常微分方程［M］.北京.高等教育出版社，2010.

［4］伍卓群，李勇.常微分方程［M］.北京.高等教育出版社，2003.

On the Singular Solution and Envelope of First-order Ordinary Differential Equations

XU Li-jun，LIAO Yong-zhi
（School of Mathematics and Computer Science，Panzhihua University，Panzhihua，Sichuan 617000，China）

The concepts of the singular solution and envelope of differential equations have always been quite abstract and complicated to understand.With the definitions and relevant theories of singular solution and envelope，as well as some examples，the present thesis purports to study the singular solution and envelope of equations，the ways of working out the singular solution and envelope of curves and to discuss how the uniqueness of solutions is broken in different ways.

ordinary differential equations；singular solution；envelope；general solution

O175.1

A

1673-1891（2016）02-0017-04

10.16104/j.issn.1673-1891.2016.02.005

2016-04-05

四川省教育厅自然科学基金项目“具依赖状态脉冲的分数阶边值问题研究”（15ZB0419）；攀枝花市科技局社会发展基金项目“攀产道地药材市场规律研究”（2015CY-S-14）。

徐丽君（1965—）女，四川眉山人，副教授，研究方向：微分方程。