例谈“一题多解”的数学教育价值

濮 安 山

(扬州大学数学科学学院，江苏 扬州 225002)



数学研讨

例谈“一题多解”的数学教育价值

濮 安 山

(扬州大学数学科学学院，江苏 扬州 225002)

“一题多解”是我国中小学数学教学基本特征“变式”教学的一种。它有助于学生对数学知识的理解和运用、有助于学生对数学方法的理解与运用、有助于学生对数学思想的理解与运用、有助于学生迁移能力的形成、有助于学生发散思维能力的提高、有助于学生良好认知结构的形成。

一题多解；数学；教育；价值

最近20多年，变式教学研究得到众多数学教育学者的重视。顾泠沅(1994)、聂必凯(2004)、张奠宙(2007)、孙旭花(2006)等对此都有深入的研究。[1]“一题多解”是变式教学重要的组成部分，得到很多一线教师的重视。[2]但存在对“一题多解”教学理论认识不清、实践的落脚点偏颇等问题。有些教师关注解题方法越多越好、解法越简洁越好，使得“一题多解”的实践教育价值没有更大地发挥作用。本文主要通过一道高考题的多种不同解法阐释“一题多解”的数学教育价值。

问题：已知正实数x，y满足x+y+3=xy，求xy的范围？(1999年高考第13题，原题是填空题，现改成解答题)

一、有助于学生对数学知识的理解和运用

毫无疑问，中学数学课堂教学的首要任务是向学生传授概念、公式、定理等数学知识。有些教师往往将这些知识信息简单地传输给学生，学生采用模仿、记忆等方法记住了，而教师缺少对知识的深度阐释，学生也理解得不够深入，从而影响了解决问题能力的形成。如果能在一题多解实施过程中反思运用的概念、公式、定理，加深对知识内涵与实质的理解，就会提高学生理解数学知识的水平，增强学生的应用能力。

1.有助于对数学概念的理解与运用

数学概念是学习其他知识的基础，也是解决数学问题的基础。学生对数学概念理解得扎实、深入，在解决数学问题过程中就容易联想到相关的概念，用不同的方法解决问题，给出“一题多解”。反之，当学生用不同的解法解决同一问题时，就会联系相应的概念，分析概念的内涵、应用条件、过程和注意事项，从而深化了对不同数学概念的认知。

2.有助于对数学定理、公式等命题的理解与运用

数学定理、公式是在数学概念的基础上运用逻辑推理获得的真命题，学生在推出这些命题时，不能马上深刻理解这些结论的本质、应用条件和注意事项，必须在解决问题中多次反复利用和思考才能掌握。而“一题多解”是从不同角度考虑问题，多次运用不同的命题解决同一问题，恰给理解与运用数学命题提供了平台和路径，下面的解法提供了例证。

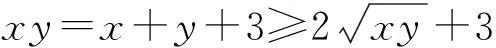
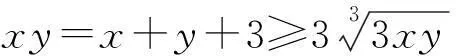
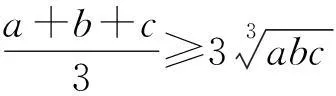
李士锜(2001)教授认为，理解数学知识的意义在于建立的表象越熟悉、越精致、越准确，就越容易记忆，也越容易提取。[3]在一题多解的解题过程中，必须运用过去学过的各种概念、定理、公式等数学知识，加深对学过知识的记忆、理解与运用，从而进一步地巩固和发展原有的数学认知结构。

二、有助于学生对数学方法的理解与运用

数学方法是中学数学教学的重要内容，新的《普通高中数学课程标准》(试验稿)也将其作为重要的课程目标。在学生数学学习过程中，数学概念、定理、公式等显性的知识是容易理解的，而数学方法和思想等隐性知识是不易掌握的。要想掌握某一数学方法，一方面听教师解读，更重要的是运用，在运用中不断加深理解和体会，下面的解法就体现了数学方法的重要性。

解法3：令xy=a，则x+y=a-3，构造方程：

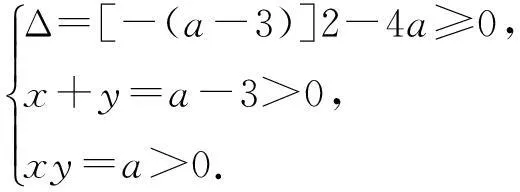
解得xy=a≥9.

可以看出，以上的解法运用了数学方法中的构造法，通过条件中两根之和与两根之积的特征，构造了关于未知量t的一元二次方程，再运用方程的知识加以解决。

通过一题多解的练习，有助于对数学方法的理解与运用，其中包括观察运用某一数学方法的条件特征、理解运用数学方法实施解题的过程与步骤、并将数学知识与数学方法有机的结合方法。

在中学数学解题中经常用到的方法有综合法、分析法、反证法、换元法、待定系数法、数学归纳法、构造法等。提高学生数学解题能力，要重视“一题多解”过程中体现出来的数学方法，在运用数学方法解决问题过程中不断深化理解，提高运用方法的能力。

三、有助于学生对数学思想的理解与运用

我国数学教育的基本特征之一是重视“双基”的教学。在修订的《中学数学课程标准》中同时也指出基本数学思想和方法的重要性，这就是通常所说的“三基”。数学思想的重要性还体现在它是思维方向、运用数学方法的指导。有些学生解决问题能力差，往往和他们没有理解和掌握数学思想有关。中学数学解题中经常用的思想包括集合的思想、函数的思想、方程的思想、分类的思想、数形结合的思想、转化的思想、极限的思想等等。此题运用数学思想解决的方法如下：

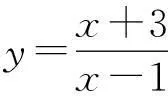
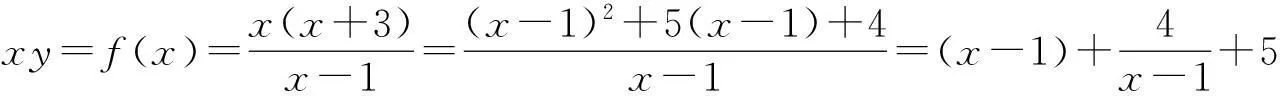
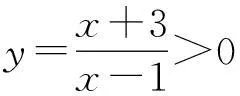
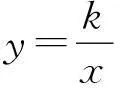
四、有助于学生迁移能力的形成

迁移是一种学习对另一种学习的影响，正迁移对促进学生的学习有重要的影响。通过“一题多解”的解题过程，既可以帮助学生进一步加深对数学知识、方法和思想的理解和巩固，同时，也能把学到的知识、方法和思想迁移到新问题的解决中，从而形成和推动学习的正迁移，进而形成良好的数学认知结构，提高学生分析问题、解决问题的能力。

上面解法4的关键体现了构造函数的思想，具体的思路是首先确定一个函数的自变量，然后构造关于此自变量的函数，最后，运用函数等数学知识解决问题。下面的几个问题都可以通过构造函数加以解决。

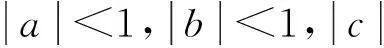
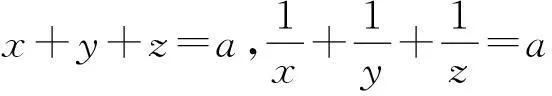
(3)已知x，y，z是实数，α+β+γ=π，求证：x2+y2+z2≥2xycosα+2yzcosβ+2zxcosγ。

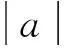
五、有助于学生发散思维能力的提高

发散思维，又称辐射思维、放射思维、扩散思维或求异思维，是指大脑在思维时呈现的一种扩散状态的思维模式，它表现为思维视野广阔，呈现出多维发散状。不少心理学家认为，发散思维是创造性思维的最主要的特点，是测定创造力的主要标志之一。而“一题多解”等方式可以更好地培养学生的发散思维能力，下面再举一例加以说明。

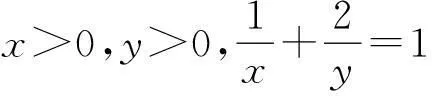
解法1(基本不等式法)

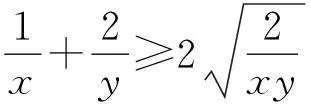
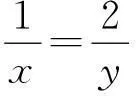
解法2(“1”的妙用)

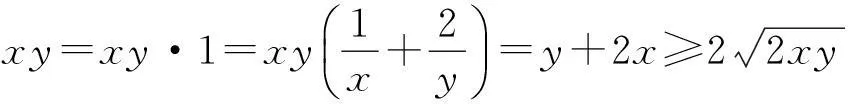
解法3(平方法)

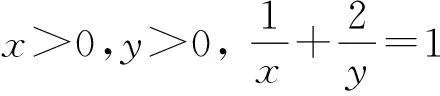
解法4(三角变换法)

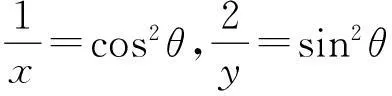
解法5(三角变换法)

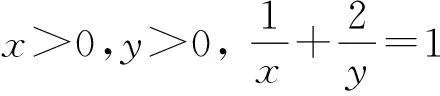
解法6(构造函数法)

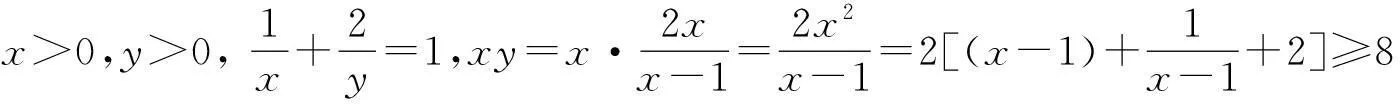
通过以上多种解法的分析，学生的思维指向不同的方向，可以多种途径去思考问题，并通过多角度、多层次的探索，提高了学生的发散思维能力，更好地培养学生数学思维的品质。

六、有助于学生良好认知结构的形成

认知结构是个人将自己所认知的信息组织起来的心理系统，良好的数学认知结构对学生知识和能力的形成是非常重要的。Bruner(1977)指出：“获得的知识如果没有完满的结构把它联在一起，那是一种多半会被遗忘的知识。一串不连贯的论据在记忆中仅有短促的可怜的寿命。”[3]

学生通过进行“一题多解”的训练，不断回忆并运用不同的数学知识、思想与方法，不断加深对已有认知结构的理解，形成新的数学解决问题的经验，进而形成新的良好的数学认知结构。通过前面的例子可以看到，学生把这个问题与不等式、函数、方程、数形结合等数学知识与方法建立了紧密的联系，从而形成一个新的数学结构。当再遇到求最值的数学问题时，学生就会回忆起已有的认知经验，运用多种方法去解决。

[1] 孙旭花.“一题多解”之再升华螺旋变式课程设计理论介绍：以三角形中位线定理推导为例[J].数学教育学报，2008，17(6)，21-27.

[2] 顾泠沅.青浦实验：一个基于中国当代水平的数学教育改革报告(上) [J].课程·教材·教法，1997(1)：26-31.

[3] 李士锜.PME:数学教育心理[M].上海：华东师范大学出版社，2001.

[责任编辑：陈学涛]

2016-03-20

江苏高校品牌专业建设工程资助项目(PPZY2015B109)；扬州大学高层次人才科研启动基金项目。

濮安山(1964-)，男，黑龙江安达人，博士，教授。

G633.6

A

1002-1477(2016)07-0057-04

[DOI]10.16165/j.cnki.22-1096/g4.2016.07.015