数学探究活动的设计与呈现方式分析
——以“无盖长方体盒子制作”为例
2016-09-01徐玉庆
徐玉庆
(1.西北师范大学教育学院,甘肃 兰州 730070;2.酒泉市第四中学,甘肃 酒泉 735000)
数学研讨
数学探究活动的设计与呈现方式分析
——以“无盖长方体盒子制作”为例
徐玉庆1,2
(1.西北师范大学教育学院,甘肃 兰州 730070;2.酒泉市第四中学,甘肃 酒泉 735000)
探究性学习是一种由科学研究的方式推演而成的学习方式,学生在探究问题的驱动下,经历探究的过程,体验探究的乐趣,体悟知识的生成。一道“做一个体积最大的长方体无盖容器”的探究活动从初中到大学经历了不断变化,充分展示了探究活动的魅力。通过对初中、高中、大学数学中出现的一道一脉相承的探究题目进行分析,从而说明探究式教学的问题设置、探究式教学模式的开展方式对于不同年龄段学生的认知水平具有不同的启发诱导作用,也为教材中探究活动的设计提供一种思路。
数学活动;探究式学习;认知方式
孔子在教学中提倡“不愤不启,不悱不发”,意思是不到他努力想弄明白而不得的程度不要去开导他;不到他心里明白却不能完善表达出来的程度不要去启发他。这充分说明了在教学中学生应该在教师的引导下经历知识的探究过程和生成过程,而不是直接告诉学生结果。新的初高中课程标准都要求学生能够积极主动地参与探究活动,提高动手能力和创新能力。[1-2]这样一种能力要求从初中到大学应该是一脉相承、逐步加强的。探究题目的设计也应根据不同年龄学生的生理和心理特征,特别是学生的认知水平,这样才能让探究性活动发挥作用。下面以“无盖长方体盒子制作”为例,展现探究活动在不同学习阶段的设计和展现方式。
一、问题的提出
北师大版七年级《数学》上册课题学习3中提出:如何用一张正方形的纸片制成一个无盖的长方体?请你动手试试看。[3](课前准备:要求每个学生在课前准备边长均为20 cm的正方形纸片和剪刀)让学生通过剪、折等动手操作活动,使他们对正方形纸片将要做成的纸盒进行想象及考察,感受纸盒的长、宽、高和原来的纸片的边长以及剪去的小正方形的边长之间的关系,并培养他们的空间观念。提出的问题在于激发学生的学习兴趣。初中学生对于问题具有强烈的求知欲,这样一个探究问题的设置并没有现成的答案和循规蹈矩的算法,问题具有开放性和创新性,有利于培养初中学生动手能力和创新能力,这也符合新课标的要求。
二、问题的解决
教师提出如下问题:
(1)如何计算纸盒的体积?剪去的小正方形的边长和折成的无盖长方体的高有什么关系?如果正方形纸片的边长为20 cm,剪去的小正方形的边长为xcm,你能用x来表示这个无盖长方体纸盒的容积吗?用公式表示。根据上面的公式,要使长方体的体积尽可能大,要求剪去的小正方形的边长x尽可能大行吗?x尽可能小行吗?为什么?
(2)在学生思考和回答上述问题的基础上进一步提出问题:既然x的值太大、太小都不能使得长方体的体积尽可能大,那么多少才比较合适呢?
(3)将全班学生按照一定的方式分成若干小组,完成下面3个任务:
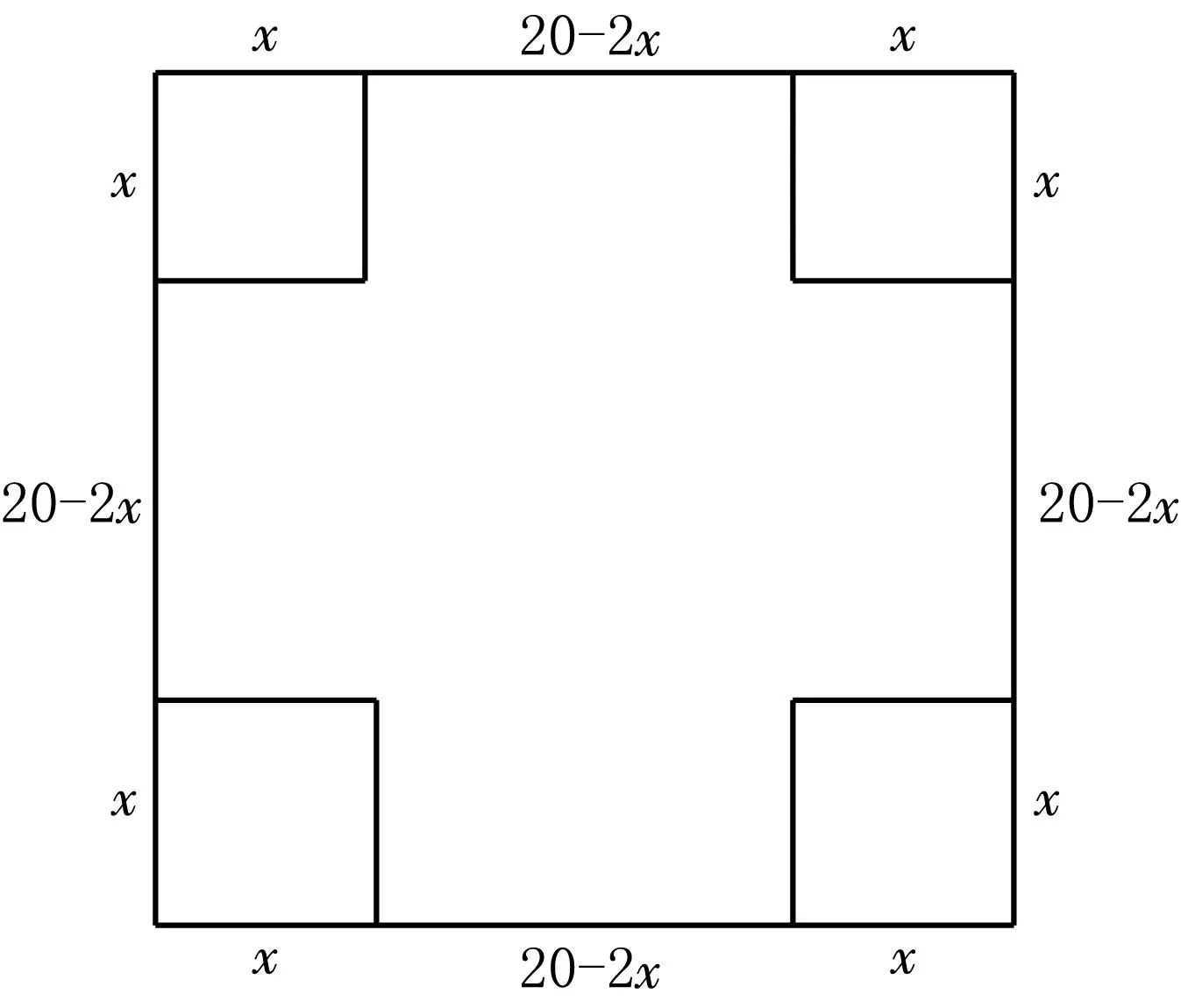
图1
如果剪去的小正方形的边长按整数值依次变化,即分别取1,2,3,4,5,6,7,8,9和10 cm时,折成的无盖长方体的体积如何变化?请你制作一个统计表,表示这个变化状况;观察自己所做的表格,你发现了什么?当小正方形的边长取什么值时,所得的无盖长方体的体积最大?此时无盖长方体的容积是多少?
假设剪去的小正方形边长为x(如图1),那么无盖长方体的体积是:V=(20-2x)2x,学生看到这个式子傻眼了,这怎么计算?这是一个关于x的三次函数,七年级学生并没有关于函数的基础。这时教师应该引导学生,让学生通过将x的值代入公式,初步体会在x取整数值的情况下,体积V的变化,其变化趋势如表1所示,发现当x=3时,体积V最大,达到最大值后,体积随着x的增大而减小。

表1 长方体体积与小正方形边长对应关系
教师:同学们观察表1的折线统计图,能够发现什么问题吗?
教师:小正方形的边长为3时体积最大吗?
学生:应该在3~4之间。
教师:那到底是多少?
教师:我们可以继续用上面列表的方法去做。
根据表1,3 表2 长方体体积与小正方形边长对应关系 由表2发现,当x=3.3 cm时,体积达到最大值V=592.548 cm3。这时教师进一步追问,那么体积现在达到最大值了吗?在上面的启发引导下,我们发现最大值应该在3.3~3.4之间,这时教师可以根据学生理解的实际情况决定是否继探究下去,可以鼓励学生在课后进一步探究。 教师进一步追问:如果在考虑不浪费材料的情况下,如何做会使得所做长方体的体积尽可能的大?长方体的最大体积还是588 cm3吗? 老师:这个体积是最大的吗?(这时学生中出现了不同的声音。) 学生:可能还有更大的体积。 老师:那么怎样裁剪就是最大的呢? 学生鸦雀无声。 老师:同学们想知道最大体积是多少吗? 学生:“想。” 老师:那同学们就要努力学习,当你们到了高中时就能够解决这个问题了。 这道初中的探究活动终于结束了,但是,那个最大体积到底是多少?在学生们的脑海中不断地萦绕,这样的探究活动根据初中生的认知水平,在老师的引导下,学生动手、动脑,完成了一次有趣的探索历程,也达到了预期的探究效果,探究题目的设计,探究问题的铺设,都为初中生探究问题打下了基础,让探究活动不再是纸上谈兵、流于形式。探究活动是一个动态发展的过程,在这个过程中,存在许多不确定的因素,所以对于初中探究活动并不能一味追求“完美”,而应该留有余地,发挥探究活动的开放性、延展性、自我调控性。[4] 那么如何设计才可以在不浪费材料的基础上让无盖长方体盒子的体积最大呢?类似的问题出现在高中数学选修2-2中。[5]高中学生的思维能力开始从形象思维向抽象思维过渡,形式逻辑思维已趋于成熟,再生性思维趋于完善。再生性思维需要解决的问题是人类认识已经解决的问题,但对于问题解决者来说,它可能是新颖的,同时高中学生在再生性思维的基础上,创造性思维也在不断发展,已经能够初步解决一些较复杂的动态变化的问题,在心理上对于复杂问题也具有一定的接受能力,所以在高中阶段学生解决这样的问题时,更愿意接受问题自身带来的挑战。[6-10] 这时我们发现x是一个无限循环小数,所以在初中探究的过程中,发现x在3.3~3.4之间,如果继续探究下去,肯定会遇到很多困难,所以在初中阶段,我们得到x在3.3~3.4之间就达到探究的目的了。当这道探究题目出现在高中时,学生很容易想到用导数这样的工具来解决,问题显得简单起来,也得到精确的结论。 图2 图3 设拼成的长方体的底面长为y,宽为x,高为z(如图3),那么长方体的体积V=xyz,问题转化为求V的最大值,这让好多学生很为难。利用面积相等可得xy+2zx+2yz=400。 这道探究题目以不同的方式出现在初中和高中阶段,教师也应该以不同的方式呈现,根据学生的认知水平和最近发展区,合理设计问题,正确把握探究的深度和广度,才能让这道题目发挥真正的价值。《高中数学课程标准》要求:“学生的数学学习活动不应该只限于接受、记忆、模仿和练习,高中数学课程还应倡导自主探索、动手实践、合作交流等学习方式”[2],这和义务阶段的课程标准是一脉相承的,在教学中应该提高学生对知识的创新能力和应用能力,让数学知识真正发挥作用。 类似的问题又一次出现在高等数学中,问题的呈现方式和解决办法也随之发生很大的变化,问题的设计要更符合大学生的认知水平。 某厂用铁板做成一个体积为V的无盖长方体水箱,问长、宽、高各取怎样的尺寸时,才能使用料最省?[12] 至此这道探究题目的讨论宣告结束,它经历了初中、高中、大学的不断演变,以一个具有较高思维价值的开放性问题呈现,以不同的形式呈现在不同年龄阶段的学生面前,问题能够激起学生的认知冲突,“迫使”学生以“科学研究者”的姿态主动参与,[13-15]通过尝试、猜测、探索,亲身感受和经历数学发现的过程,问题涉及学生的发散思维、创新思维、批判思维,所以对学生的思维品质具有较高的要求。教师根据不同年龄学生的生理和心理特点,根据学生不同的认知水平,在不同阶段设计了不同的问题,在不同阶段让探究学习发挥了它真正的价值,让学生在探究学习中寻找到了学习的乐趣,找到了学习的真谛,发现了学习与生活之间的联系,培养了他们解决复杂问题的能力,端正了对于探究问题的认识,提高了他们解决问题的能力,在探究中发掘自己的潜能,在探究中不断地创新,只有这样学生掌握的知识才是生动的、鲜活的、可迁移,学生的数学素养才能得到质的飞跃。 [1] 教育部.全日制义务教育数学课程标准[M].北京:北京师范大学出版社,2011. [2] 教育部.普通高中数学课程标准(实验) [M].北京:人民教育出版社,2003. [3] 义务教育课程标准试验教科书·数学·七年级(上册)[M].北京:北京师范大学出版社,2014. [4] 宁连华.数学探究教学设计研究[J].数学教育学报,2006,15(4):39-41. [5] 严士健,王尚志.普通高中课程标准实验教科书·数学(2-2) [M].北京:北京师范大学出版社,2008. [6] 张奠宙,宋乃庆.数学教育概论[M].北京:高等教育出版社,2009. [7] 顾继玲,张新华.初中数学教材探究活动设计的思考[J].数学教育学报,2012,21(3):63-66. [8] 曾小平,汪秉彝,吕传汉.数学“情境—问题”教学对数学探究学习的思考[J].数学教育学报,2009,18(1):44-47. [9] 吕世虎,王积建.初中数学探究式教学的实验研究[J].数学教育学报,2005,14(4):52-55. [10] 涂荣豹.谈提高对数学教学的认识[J].中学数学教学参考,2006(1/2):2-8. [11] 刘云,张广祥,黄永明.高中数学必修教科书中的数学探究活动分析[J].数学教育学报,2012,21(5):76-79. [12] 陈纪修,於崇华,金路.数学分析[M].北京:高等教育出版社,2004. [13] 龙开奋.数学探究课题研究 [J].数学教育学报,2008,17(4):41-44. [14] 陈亮,朱德全.数学探究教学的实施策略 [J].数学教育学报,2003,12(3):36-39. [15] 徐章韬,梅全雄.论基于课堂教学的数学探究性学习 [J].数学教育学报,2013,22(6):54-57. [责任编辑:陈学涛] 2016-03-16 甘肃省教育科学规划“十二五”课题GS[2014](GHB1360)。 徐玉庆(1985-),男,甘肃武威人,硕士研究生,中学二级教师,酒泉市肃州区骨干教师。 G633.6 A 1002-1477(2016)07-0053-04 [DOI]10.16165/j.cnki.22-1096/g4.2016.07.014
三、问题的进一步解决
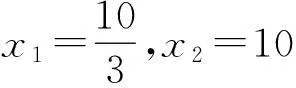
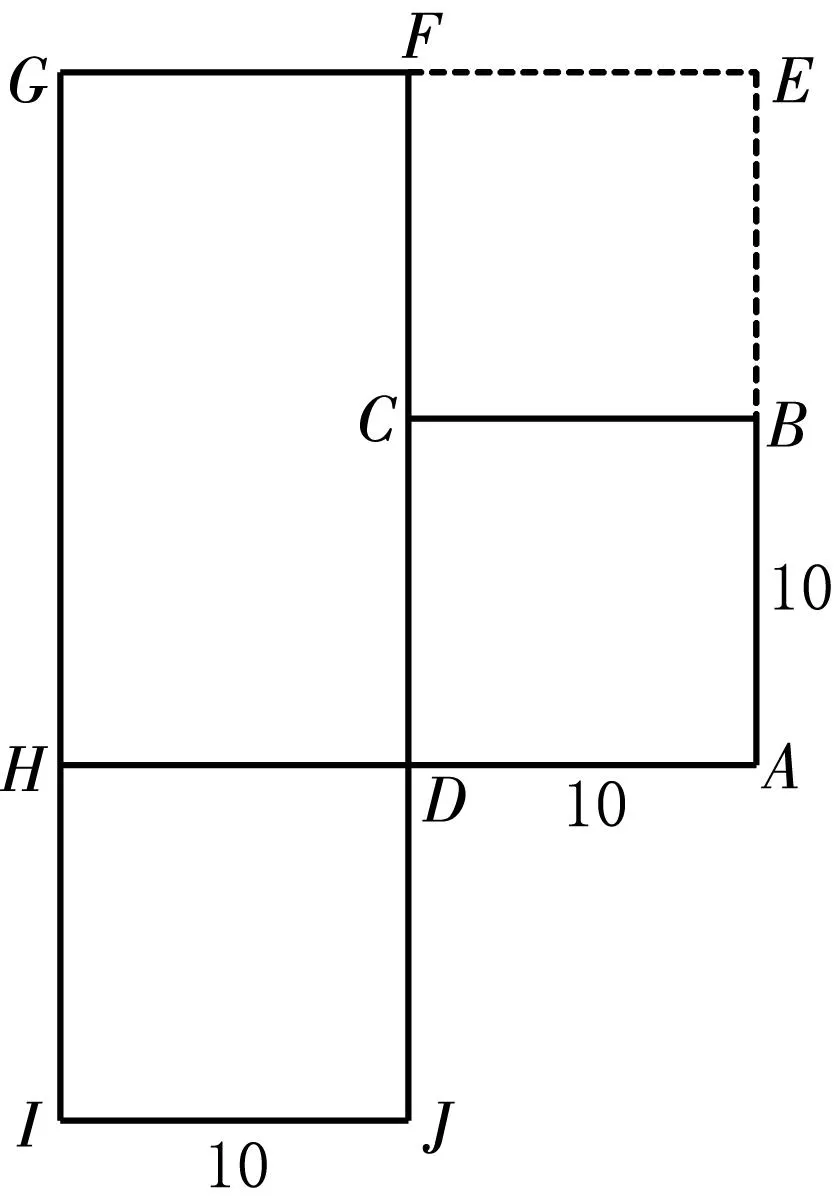
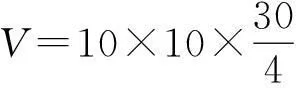
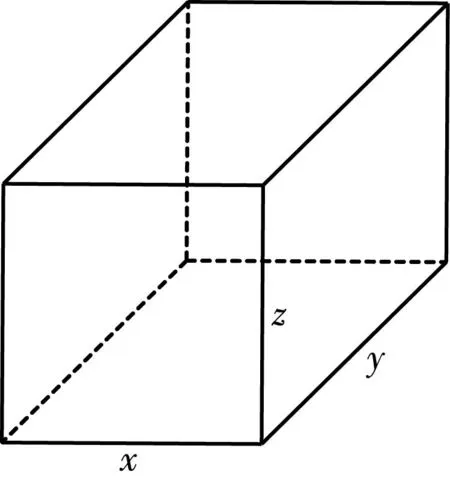
四、问题的升华
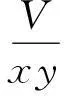
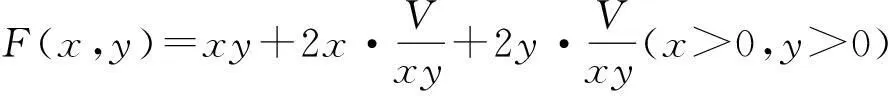
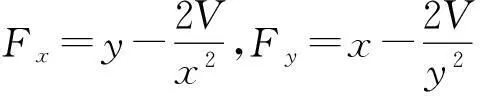
五、结论和启发
