例析初中数学的多解问题

曾凡炳

摘要：在中学新课程的背景下，老师们对于学生的培养也不仅仅局限于会做或者能做上，而更多的是在思维方式上，培养学生们的实践能力、创新精神，多角度考虑问题的能力成为了初中阶段各科教学活动的最终目标。正如现在挺火的一句话：创新，是数学课堂永恒的主题。而多解问题愈加成为考察的重点，在多解问题中，我们不仅能够考察学生的细心仔细的程度，更加可以考察学生的逻辑思维能力。多解问题中我们需要从各个角度中看待这个问题，考察的点特别多，从而获得现在老师们的青睐。如果能够以点概面，在多解问题中对学生进行知识点的指导，并加以科学思维角度的分析，这样将会更加有利于学生对知识点的把握。

关键词：初中数学多解问题；一题多解；教学研究；新思路新模式；发散思维

一、常见的多解问题圆的多解问题

已知点P到圆O上的点的最大距离是6cm，最小距离是2cm，则圆的半径r=？

解析：分析题意可知，点P不在圆上，因此，应对点P与圆O位置进行分类 。分点P在圆O内和圆O外这两种情况进行讨论。做出如图所示，点P在圆内和点P在圆外。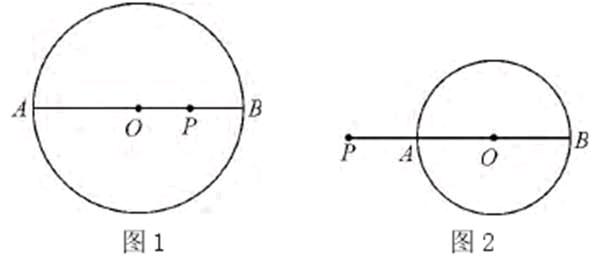

解：当点P在圆0内时，如图1所示。

P A = 6 c m，P B = 2 c m，则A B=6+2=8（cm），所以r=4cm

当点P在圆0外时，如图2所示，PA=2cm ， PB=6cm，则A B=6-2=4（cm），所以r=2cm

综上所述，r=4cm或2cm

总结来说，确定了点与圆的位置关系，从本质上来说就是确定点到圆心的距离与半径的大小关系。一般的多解问题中并不会明确点与圆的关系，所以应该考虑点在圆上、圆内、圆外这三种可能。而在有些题目中，需要使用数形结合的手法进行讨论或者圆的角度问题，这些都是出题的的重点。但是万变不离其中，只要记住重要的定理命理，多解问题也就变得非常简单了。

三角形的多解问题；若等腰三角形腰上的高等于腰长的一半，则底角为分析题中等腰三角形可能是锐角三角形也可能是钝角三角形，因而其腰上的高可能在三角形内也可能在三角形外，同学们受习惯思维的影响，往往只考虑前一种情况，所以答案只有75°而缺少15°。

已知 ABC内接于⊙ O，∠BOC=100°，则∠ BAC=

分析：题中圆心O与A点可在弦BC的同侧，也可在弦BC的两侧，许多同学往往忽略后一种情形，答案中只有50°而少130°。

总结来说，解答三角形的多解问题时，同学们往往会产生思维定势或者审题不清，导致漏解和错解。三角形的边长和角度问题是解答的重点，而这类题往往会把三角形和圆结合起来，把两个知识点结合起来，多解中包含着错解，这样在无形之中就更增加了难度，成为热点问题。

方程的多解问题

例4、y2+（k+ 1）y+ 9是完全平方式，求k.

分析 完全平方式有两种形式，同学们往往只注意k+ 1= 6，忽略k+ 1=- 6情形

例5、如果x2= 25，则x= ？

分析 本题实质是求25的平方根，应为x=± 5.但有些同学往往忽略x=- 5，说明对平方根概念理解得不够深刻.

例6、有两个连续的奇数，两个数字之积是483，求出这两个奇数。

分析 这个题的多解解法的核心就是两个连续的奇数相差为2，相乘为483，把握住方程的等量关系，变得也只是未知数的形式而已。当我们把方程的等量关系都找出来的时候，就可以减少漏解了。

解法一：通过对问题的分析得出，较小的奇数为x，则与这个较小奇数想连续的另一个奇数大小是x+2，则得出x（x+2）=483，可以得出两个奇数的值为21，23或者-23，-21（很多时候同学们会忽略这种情况）

解法二：设两个奇数的大小分别为2x+1，2x-1，同样可以得出结果；还可以较大的奇数为x，较小的奇数为483/x，方程为-483/x=2.

二、一题多解模式下的课堂学习

1、教师与学生的“双向选择”。使用多解模式，教师们在讲课过程中展现的解题思路、解题方法会使学生们影响深刻。教师的示范性作用，通过例题的讲解，让学生们体会到一题多解的趣味性，进而让他们变换自己的解题思路，更好的解决问题。对于学生来说，一题多解代表着一种合作能力，同学们对于同一道题总是有着自己不同的想法，各自独特的解题思维才是多解题型最好的答案，而这就需要学生们进行合作，提升自己的发散性思维。

其实，在多解问题这个平台上，教师通过一个带头、领导的作用，把多解的思想传递给学生，引导他们进入正轨，让学生合作探讨一个题型，教师同样也获得了成长。师生双向选择，逐步展现了多解问题的魅力，可以说，多解问题是学生在理科上的引路人。

2、发散式思维的重点培养。传统教学中，老师们只是要求学生“怎么做”，而不会告诉学生“为什么这么做”，死板，约束学生的思想。新课标中，我们不只是告诉学生这个题怎么做，而且要告诉他怎么来的，这就是新课标，新思维。多解问题是一个创新，在中学课堂上，一题多解式的问题架构对于学生的成长起到的作用无疑是巨大的。

三、结语

初中数学中有各种各样的多解问题，解答这类多解问题，就要求学生必须有缜密细腻的思维，扎实的基础知识和丰富的想象能力，所谓“见多识广”，学生应该在掌握了理论知识的同时，广见题型，理论与实践相结合，这样才能有更好的发展。同时，汲取发生漏解错解的教训，提高准确率，

一题多解式教学，体现的不只是一个题型，这也是新课标改革的进步性发展，是里程碑式的教育建设，这个需要教师和学生共同 ，积极探索学习数学的奥妙，在探索中发现数学解题的多样性和趣味性。当然，不论教育模式，教育方法如何变化，教育的最终目的就是提升学生的综合能力，培养全面素质，这点毋庸置疑。

参考文献

[1] 钱小强. 例析初中数学的最值问题[J]. 新课程学习（上），2014，02：84-85.

[2] 林郑娜. 初中数学解题中《圆》中易错问题例析[J]. 中国科教创新导刊，2014，14：74+76.

[3] 冯竹林. 初中学生数学解题错误的调查与研究[D].云南师范大学，2009.

[4] 李亚章. 例析初中数学竞赛中的高斯函数问题[J]. 初中数学教与学，2012，05：30-32.