《数列求和》基本方法与类型探析

吕　骥

(鄂南高级中学，湖北　咸宁　437100)



《数列求和》基本方法与类型探析

吕骥

(鄂南高级中学，湖北咸宁437100)

数列作为一种特殊的函数，是反应自然规律的基本数学模型，是高中数学的重要内容之一，在高考和各类数学竞赛中都占有重要的地位，特别是回归全国卷以后，数列的深度、广度和重要性更是上了一个台阶。数列求和又是数列当中的一种基本运算，是数列版块的重中之重，是数列里的必考内容，因此必须引起广大师生的特别重视。想要攻克这一重难点，必须掌握数列求和的常见方法和基本类型，以下分别来做介绍：

一、公式法求和

公式法主要是用于解决最基层的数列求和问题的，等差数列和等比数列作为两种最基本的数列，自然要熟记其求和公式，除此之外，前n个正整数的平方和、立方和公式也是需要熟记的，并没有太多的技巧。

以下就是一些需要记忆的公式：

(1)等差数列前n项和公式:

其中，Sn为等差数列{an}的前n项和，a1为其首项，d为其公差。

(2)等比数列前n项和公式：

其中，Sn为等比数列{an}的前n项和，a1为其首项，q为其公比，要注意对其公比q是否为l进行判断。

(3)前n个正整数的和：

前n个正奇数的和：

Sn=1+3+…+(2n-1)=n2

前n个正偶数的和：

Sn=2+4+…+2n=n(n+1)

前n个正整数的平方和：

前n个正整数的立方和：

其中，前n个正整数的和、前n个正奇数的和、前n个正偶数的和直接用等差数列的求和公式来证明；前n个正整数的平方和、前n个正整数的立方和可用数学归纳法证明。

例：(1)已知数列{an}的通项公式an=-2n+11，如果bn=|an|(n∈N)，求数列{bn}的前n项和。

(2)设等比数列{an}前n项和为Sn，若S3+S6=2S9，求数列的公比q

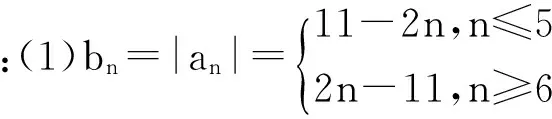
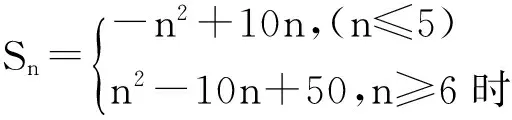
(2)若q=1则S3+S6=9a1,而2S9=18a1,与S3+S6=2S9矛盾，故q≠1，

得2q9-q6-q3=0,2(q3)2-q3-1=0,

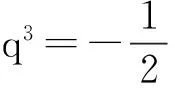
方法小结：一旦确定了某数列是等差数列、等比数列或是与前n个正整数相关的求和问题是，就可考虑使用公式法求和。

二、倒序相加法求和

倒序相加法求和是从等差数列求和中抽象出来的一种方法，思路很重要，但使用频率并不是很高，往往会与函数求值联系在一起。

例：求数列{2n+1)Cnn}的前n项和.

解：记Sn=Cn0+3Cn1+5Cn2+…+(2n+1)Cnn

则Sn=(2n+1)Cnn+(2n-1)Cnn-1+…+3Cnn-1+Cn0=(2n+1)Cn0+(2n-1)Cn1+…+3Cnn-1+Cnn

两式相加得，2Sn=(2n+2)(Cn0+Cn1+…+3Cnn-1+Cnn)=2(n+1)·2n

故Sn=(n+1)·2n

方法小结：倒序相加法求和是基于推导等差数列求和而派生的一种求和方法，使用的特点是，与首末等距的两项和相等。

三、错位相消法求和

错位相消法是基于等比数列求和推导出来的一种求和方法，需要注意在和式两边同乘的数是否为1，这是一种考察频率极高的求和方法，要特别重视。

例：(1)已知数列{an}是等差数列，且a1=2,a1+a2+a3=12，.

(Ⅰ)求数列{an}的通项公式；

(Ⅱ)令bn=an·3n(n∈N*),，求数列{bn}的前n项和的公式.

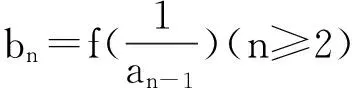
解: (1)(Ⅰ)∵a1=2,a1+a2+a3=12

∴3a1+3d=12,即d=2

∴an=2+(n-1)·2=2n.

(Ⅱ)由已知：bn=2n·3n

∵Sn=2·3+4·32+6·33+…+2n·3n+1

3Sn=2·32+4·33+…+2(n-1)·3n+2n·3n+1

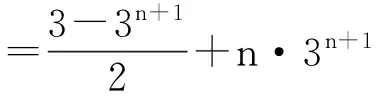
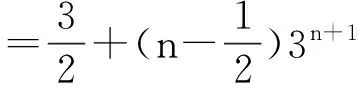
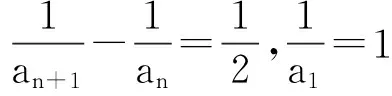
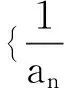
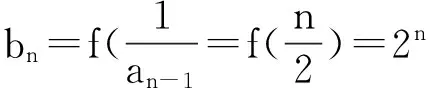
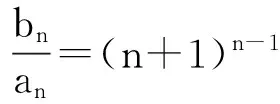
Tn=2×20+3×21+4×22+…+(n+1)×2n-1

①

2Tn=2×21+3×22+…+n×2n-1+(n+1)×2n

②

∴Tn=n·2n

方法小结：形如an=bn·cn的数列{an}可考虑使用错位相消法求和，其中{bn}为差数列，{cn}为等比数列。错位相消法求和有很多计算方面的易错点，对计算的精细要求程度非常高，从常规教学情况来看，许多学生知道方法但不一定能算出准确的结果，是考试中的一个拉分点。

四、裂项相消法求和

数列{an}的通项如果能拆成形如an=f(n)-f(n-k)(k=1,2…)的形式，那么在求和时就可以进行相邻项(或相隔几项)的相互消去，从而结果只存在有限几项，达到求和目的。其中通项公式为分式和根式的采用裂项相消法求和较多。

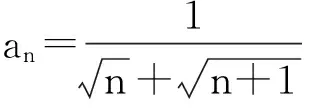
(2)已知等差数列{an}满足：a3=7，a5+a7=26,{an}，的前n项和为Sn。

(Ⅰ)求an及Sn；

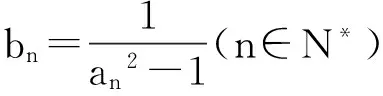
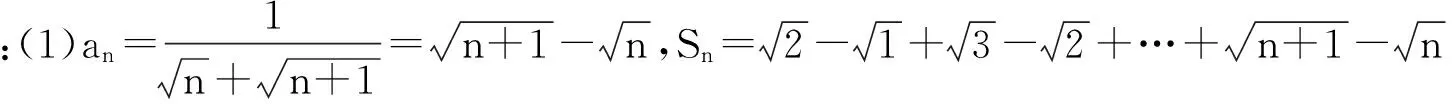
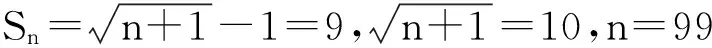
故该数列的前99项之和等于9，

(2)(Ⅰ)设等差数列{an}的公差为d，

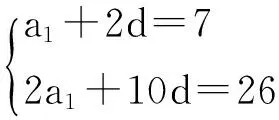
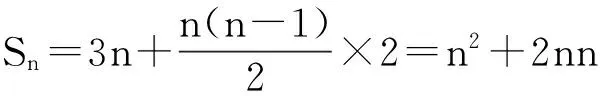
(Ⅱ)由(Ⅰ)知an=2n+1，

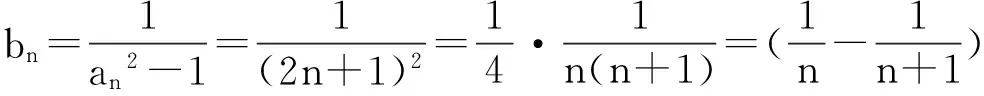
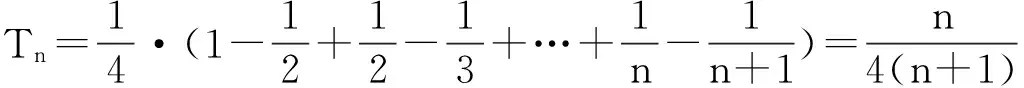
方法小结：常见的裂项方法有：

(4)an=Sn-Sn-1(n≥2)，其中Sn为数列{an}的前n项和

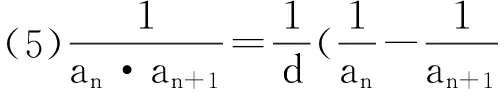
五、并项相加法求和

形如{(-1)n-1·an}(其中{an}为等差数列)的数列可考虑用并项法求和，求和时注意对n的奇偶性进行分类讨论.

例：(已知数列{(-1)n-1(4n-3)}的前n项和为Sn，求S15+S22-S31的值。

∴S15=29,S22=-44,S31=61,

∴S15+S22-S31=-76

方法小结：在并项求和时要注意：

(1)相邻两项一组，如果项数为奇数，那么会留出一项，项数为偶数，那么刚好分组。所以要对项数进行奇偶的分类讨论；

(2)在项数为偶数的求和过程中要注意的取值变化不再是1,2,3,…，而是2，4，6，…，所以求和时的项数会对应发生改变；

(3)对项数为奇数的求和可利用前面偶数求和的结论，可以大大简化求和过程.

六、分组法求和

如果数列{an}的通项公式是前几种可求和形式的和与差，那么在求和时可将通项公式分成这几部分分别求和后，再将结果进行相加减。

例：(1)已知an=n(n+1)(n+2)，求数列{an}的前n项和Sn。

(2)求和：Sn=(a-1)+(a2-2)+…+(an-n),a为非零常数。

解：(1)an=n(n+1)(n+2)=2n3+3n2+n，

∴Sn=2(13+23+…+n3)+3(12+22+…+n2)+(1+2+…+n)

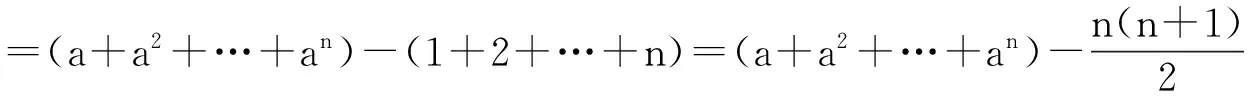
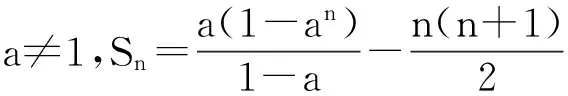
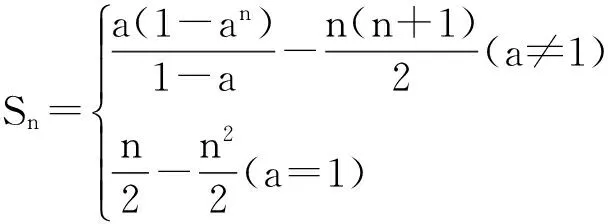
方法小结：若数列{an}本身不是等差数列，不是等比数列，也不具备整体使用倒序、裂项、错位、并项求和的特点，可考虑将其适当拆开，分成几个等差、等比或常见的数列分别求和，再将其合并。

文章编号：2095-4654(2016)05-0144-03

* 收稿日期：2015-12-20