满足故障可诊断性的传感器配置方法

刘丽桑，胡晓强，彭侠夫*，万斌浩

(1.福建工程学院信息科学与工程学院,福建福州350118;2.厦门大学航空航天学院,福建厦门 361005)

满足故障可诊断性的传感器配置方法

刘丽桑1，胡晓强2，彭侠夫2*，万斌浩2

(1.福建工程学院信息科学与工程学院,福建福州350118;2.厦门大学航空航天学院,福建厦门 361005)

摘要：以系统的部件级物理结构或数学模型为对象,基于有向图技术提出了非线性系统满足故障可诊断性的传感器优化配置方法．在对有向图中故障检测与分离概念进行定义的基础上,设计了一种最小传感器配置方法,讨论了进一步优化的方法:1) 按照实际配置情况,以价格、质量、体积与功耗混合的最小代价原则替代最小数量原则,给出了以最小配置为出发点的优化搜寻算法;2) 考虑最小配置子集中某传感器发生故障导致的故障可诊断性功能缺失,设计了一种后补偿方法与一种直接补偿的改进贪婪算法．并以卫星的动量轮系统为例进行仿真,仿真结果验证了配置方法的有效性．

关键词：传感器配置;故障诊断;有向图

在现代化的工业控制等领域中,故障诊断正受到越来越多的关注与重视．对系统实际过程行为测量的需要,决定了故障的可诊断性严重依赖于系统中配置的传感器类型与数量．传感器优化配置的研究始于20世纪70年代末,但相较于故障诊断领域,传感器优化配置的研究还相当不充分,而且在理论上更不完善．

针对线性时不变动态系统,彭涛[1]提出了一种基于传感器最优配置的混合H-/H∞故障检测观测设计方法,对建立的模型分别采用线性矩阵不等式(LMI)技术、Pareto遗传算法等优化方法获得系统设计的最优解．Rao等[2]从系统的实际物理结构中导出系统的有向图,通过因果分析,将其转化为故障与测点关系的二分图,进而求出最小传感器配置子集．刘睿等[3]以航天器部件为例对上述方法进行了工程上的实现．Commault等[4]基于线性系统的状态空间描述,将系统故障与不确定扰动作为系统的输入,讨论了有向图最大链路的规模与系统故障可诊断性的关系,将有向图进行了等价分解与降维后实现了对传感器的优化配置．戴文战与陈杰等[5-6]使用故障传递矩阵,将故障传播有向图从二值定性分析量化为数值分析．Azam等[7]引入故障发生概率的概念,提出了一种基于优化问题的模型,通过有效的算法训练,确定了对多故障组合诊断的传感器配置．Rosich等[8]同样基于优化问题的方法,以一种增量迭代算法,避免了Sarrat等[9]所使用的穷举法中出现的计算复杂度随候选传感器数量的增加而呈现指数增长的缺点,同样实现了最小成本的传感器配置．文献[10-12]对于线性或非线性微分代数方程,使用Dulmage-Mendelsohn分解技术,将系统的微分代数方程组分为3个部分:过约束部分、完全约束部分与欠约束部分．针对完全约束部分,通过提取测点之间的偏序关系,以最少传感器数量实现了该部分故障可诊断配置．

本文使用有向图方法,以跟踪型贪婪算法求取满足系统故障可诊断性的传感器最小配置子集．以此为基础,考虑质量、体积、功率等条件的约束,进一步分析了更符合实际情况的最小代价传感器配置．针对所配置传感器发生故障的情况,提出了冗余补偿配置方法与一种直接补偿的改进贪婪算法．最后,以动量轮系统为例,对方法的有效性进行了验证．

1传感器的初步优化配置

1.1基本概念

在使用有向图进行满足故障可诊断的传感器配置问题中,我们将故障的可诊断性划分为两个层次:故障可检测性与故障可分离性．现分别给出图论中对故障可检测与可分离的定义．

假设系统中共有k个既定故障,且在任意时刻最多只有一个既定故障发生．共有n个待选测点,组成集合S,其中选取了m个测点配置传感器,组成的测点集合为Z,显然有0≤m≤n,Z⊆S．

故障可检测:当系统中某故障Fi发生时,其将对一系列的测点产生影响,将受其影响的测点集合记为Ai(Ai⊆S)．当且仅当Ai中至少有一个测点配置了传感器时,即Ai∩Z≠ø时,故障是可检测的．

故障可分离：对于系统中存在的两个不同作用位置的既定故障Fi与Fj,在分别满足可检测的基础上,当两者影响的测点集合的交集相对于其并集的补集中至少有一个测点配置了传感器时,可保证两个故障的系统输出存在差异[2]．因此,可以在所有既定故障分别满足了可检测性的基础上定义故障可分离性:故障Fi影响的测点集合为Ai,另一个故障Fj影响的测点集合为Aj,当两个测点集合的交集相对于其并集的补集Bij中至少有一个测点配置了传感器时,即存在关系式Bij∩Z≠ø时,故障Fi与Fj可分离．若故障两两可分离,则系统故障是可分离的．

传感器的配置问题可描述为如下形式:按一定的准则(如:个数最少或成本最低等)从测点候选集合S中选取若干个测点组成传感器配置集合Z,以满足上述故障可检测性与可分离性要求．

1.2故障传播有向图的建立与简化

故障传播有向图定性反映了系统的内部结构,同时亦反映了所研究的故障集合作用于系统的位置及其影响的传播模式,是本文研究传感器在满足系统故障可诊断性的基础上实现优化配置的基础与出发点．

获取故障传播有向图的方法有2种:

方法1:将系统的状态空间描述或者微分方程组转化为有向图．以方程组中出现的变量以及微分变量作为节点建立故障传播有向图,对于微分方程右边的每一个变量,其对应的节点都存在一条有向弧指向左边微分变量对应的节点;由于微分变量影响相应的状态变量,前者的节点也应存在一条指向后者节点的有向弧．若考虑如下非线性微分方程组：

(1)

其中，x1(t),x2(t),x3(t)为系统的状态变量,w1(t),w2(t),w3(t)为系统的故障变量,各故障变量之间相互线性独立地进入状态方程．建立的故障传播有向图如图1(a)所示．

方法2:直接通过系统的部件级结构图获取系统的有向图．以每一个部件的输出作为一个顶点,若一个输出作为某部件的输入对该部件的输出具有影响,则在相应的顶点之间存在一条有向弧．该种方法直接从系统的实际结构出发,建立的有向图的规模一般会大于第一种方法建立的有向图模型,其在传感器配置过程更加复杂的同时,亦增加了候选测点的选择．

图1　公式(1)所建立的故障传播有向图Fig.1The fault propagation digraph of formula

1.3最小传感器配置

根据1.1节中的定义,在进行传感器配置前,需确定每个故障的检测点集合与两两故障间的分离集合,即对故障传播有向图进行因果分析．

所谓的故障因果分析,要求分别从每一个故障节点Fi出发,沿有向弧搜寻下一个顶点,将找到的顶点编号保存之后继续搜寻;若遇到分叉口,保存其下标,沿一条路径搜寻结束后返回分叉口继续搜寻;当搜寻到只有入路没有出路的顶点后,沿该方向的搜寻结束．最后将搜寻得到的该故障所能够影响的所有测点组成故障的检测集合:

Ai={Sj|若存在一条路径从Fi到Sj}.

(2)

其中i=1,2,…，k,j=1,2,…，n．在确定了每一个故障的检测集合之后,可以通过对比两两检测集合的不同,得到故障分离集合

i,j=1,2,…，k且i≠j.

(3)

然后以故障检测集合Ai与故障分离集合Bij为根节点,各测点为顶节点建立二分图．若故障检测集合Ai分离集合Bij中包含的某测点,则在相应集合与该测点之间存在一条有向弧指向该测点．

上述预处理结束后,使用跟踪型贪婪算法[2]求取满足故障可诊断性要求的最少数量传感器配置方案:

1) 根据最大有效入度原则选取配置测点(所谓有效入度是指测点的实际入度减去其存贮的入度,表示了根节点可新增覆盖的根节点数)．

2) 标记选择测点所覆盖的根节点,并从二分图中删除再次覆盖的根节点与之前标记的测点之间的弧(即消去之前标记的测点可通过这次标记的测点实现对根节点的检测与分离的功能)．

3) 存贮这次标记的根节点与未标记的测点之间的弧．

4) 判断测点是否覆盖了所有的根节点．是则转5),否则返回1)．

5) 将具有实际入度的标记测点组成最小配置子集．

现以一个简单的例子加以说明．考虑图2所示的某故障传播有向图,为方便计算机的实现,将其故障二分图表示为表1所示的邻接矩阵形式．5个测点的有效入度分别为:8,9,8,5,8(该处使用从左到右规则),第1次配置测点选S2;第2次,有效入度分别为2,0,4,2,4,选S3为配置测点;未标记的3个测点的有效入度为0,1,1,随意选取S4为配置测点,则二分图的所有根节点得到标记,此时标记的3个测点的剩余入度分别为3,6,5．由上述方法可求得图2所示系统的最小传感器配置方案为Z={S2,S3,S4},且其配置方案不唯一,该配置可实现各个故障的检测与R1,R2除外的各故障分离．

Ri为讨论的系统故障；Si为系统的候选传感器配置测点,i=1,2,3,4,5.图2　某系统故障传播有向图Fig.2The fault propagation digraph of a system

2传感器的进一步优化配置

2.1最小代价配置

在1.3节中,讨论了使用跟踪型贪婪算法求取系统最小传感器配置集合的一般步骤．但在实际应用中,由于受到各种客观条件的约束与限定,最小传感器配置集合不一定是最优的,甚至并不一定是可行的．因此,需要在最小传感器集合的基础上,采用一种类似内点法的方法对配置问题进一步优化．所谓的内点法,是一种针对有约束非线性规划问题的优化搜索方法．其中心思想是迭代序列从某个给定的内点(可行解)出发,不断地逼近最优解．以传感器配置的综合代价为问题的目标函数,以配置满足系统故障可诊断为约束条件,将最小代价配置描述为优化问题形式．

表1　图2系统的故障二分图

以列向量P,Q,V与E分别代表各个传感器的价格、质量、体积、功耗，利用专家知识对各个指标的相对重要性进行评估,确定各指标的权重,形成权重列向量L．最后以二值列向量C表示传感器的配置情况,其中

则目标函数可表示为如下形式:

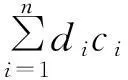
(4)

其中di为第i个测点的综合代价,di=l1pi+l2qi+l3vi+l4ei,n为候选测点个数．而对于系统必须配置的测点,人为将其代价置为0;对于某指标超出系统设计范畴的传感器,将其代价置为充分大．

观察目标函数的表达形式,可以将S值视为n维赋范空间内某点的车比雪夫范数．对于二维空间,车比雪夫范数意义下的等值线为d1c1+d2c2,对于三维空间,车比雪夫范数意义下的等值面为d1c1+d2c2+d3c3．则对于n个候选测点,S的数值应位于对应的n维空间上的某一等值超平面上．

设计搜寻算法为：

1) 以最小传感器配置子集(m个传感器)总代价所在的等值超平面为出发点,选择两两传感器配置代价之差的最大公约数作为搜寻步长h,向原点方向收缩等值超平面至代价最小的m个传感器的代价总和P2．

2) 在每一个超平面以内搜寻接近于超平面且使系统满足故障可诊断性的测点子集．如若找到这种测点子集,则其在总代价原则下优于最小配置子集．

2.2有向图的降维

最小代价配置程序大量使用递归调用,这使得程序对大数据的处理不仅需要一个较大的堆栈对现场进行保护,而且需要耗费大量的时间．因此,在预处理阶段通过某些方法人为的降低问题的规模就显得十分有必要．基于对二分图邻接矩阵的分析,可以实现在一定程度上对问题进行降维．

1) 对比二分图邻接矩阵的每一行,合并对于测点的影响完全相同的两行．

2) 对比二分图邻接矩阵的每一列,找出对于检测集与分离集响应完全相同的测点,将它们合记为一个测点．

3) 搜寻二分图邻接矩阵的每一行,找出入度为1的根节点,则对应的测点即为必须配置传感器的基本测点,所有的基本测点组成基本测点集,剩余测点组成剩余测点子集．

4) 将与基本测点集中任意测点相关联的每一个根节点删除,记剩余根节点组成的集合为Y．

配置问题即可化为:从剩余子集中按某一原则选取配置子集,以完全覆盖剩余根节点集Y．

图2所示的系统二分图经过降维后的二分图邻接矩阵如表2所示,其实质上是将故障1与故障2合并为一个故障．

表2　图2系统的降维故障二分图

2.3传感器故障补偿配置

对于一个系统,其传感器可分为2种类型：第1种是为了实现反馈控制所配置的传感器,这种传感器是系统正常运行的重要组成部分,可通过上述故障传播有向图,将其作为系统的一部分进行讨论；第2种是为了实现系统故障诊断所配置的传感器,这种传感器的故障,虽然并不会直接影响系统的正常运行,但却严重影响了系统故障的检测与分离．当系统某一故障发生时,可能由于相关传感器的故障而无法对发生的故障进行诊断,使该故障长期潜伏于系统之中．对于这种传感器的故障,可以通过冗余配置,消除其影响．下文在最小传感器配置的基础上对该种传感器的故障补偿问题进行研究．

假设某传感器故障的输出值恒定不变,将不能反映系统的故障发生，那么由于该传感器故障,在故障二分图中对应测点所覆盖的根节点就有可能重新暴露出来．传感器故障补偿配置的核心是确定暴露出的检测或分离功能并将其重新覆盖．所以设计传感器故障补偿配置的步骤如下：

1) 对最小配置集合中的每一个传感器,在假设其故障的基础上,分析配置集合对于系统各故障的输出响应,确定损失功能．若某故障的响应为0,则系统失去了对该故障的检测能力与分离该故障与其他故障的分离能力;若不同故障的响应相同,则系统失去了分离这2种故障的能力．

2) 将各传感器故障所损失的诊断功能(Ai,Bij)定义为补偿集合G,并以G中的元素为根节点,测点为顶节点,构造补偿配置的二分图．

3) 使用跟踪型贪婪算法,求解出最小补偿配置集合．

考虑表2所示的降维系统，其某一最小配置方案为Z1={S2,S3,S4}．分别假设3个测点的传感器发生故障,则失去的诊断功能为M1={A4,A5,B14,B15,B34,B35,B45},需要的补偿配置为{S3,S5}．而对于另一种配置方案Z2={S2,S3,S5},M2={A3,B13,B34,B35},需要的补偿配置为{S4}．

由上述讨论可以看出,不同的传感器最小配置方案,在其传感器发生故障的情况下，损失的故障诊断功能数量相差巨大,所需要的补偿配置也因此不尽相同．分析配置测点与故障诊断功能之间的关系,列于表3,可以发现,传感器发生故障损失的故障诊断功能都是在现有配置方案下只实现了一次覆盖的功能项以及与损失的检测项相关的分离项．

表3　配置测点与诊断功能二分图

注：表中的×表示该检测或分离功能丧失;空白表示功能仍然可以实现.

现给出一种改进的贪婪算法,其中心思想是在第1次进行传感器配置时即保证故障诊断功能的2次覆盖,则当任意某一配置传感器故障时,亦可保证整个系统诊断功能的完整性．其过程如下:

1) 根据最大有效入度原则(实际入度与存贮入度之差)选取配置测点,若有多个测点有效入度最大,则优先选择未标记测点．

2) 标记选择测点与其所覆盖的所有根节点.

3) 若某根节点为第2次标记,存贮该根节点与未标记的测点之间的弧,并将其从待定根节点集合中删除．

4) 若某根节点多于2次标记,从二分图中删除该根节点与之前标记的测点之间的弧．

5) 判断待定根节点集合是否为空．是则转6),否则返回1)．

6) 将具有实际入度的标记测点组成最小配置子集．

考虑表2所示的降维系统．5个测点的有效入度分别为:4,6,6,4,6,随意选取(该处使用从右到左的规则)S5为配置测点;第2次选择时,5个测点的有效入度仍为:4,6,6,4,6,但依据未标记者优先,选择S3为配置测点;第3次,各测点有效入度为:3,4,3,3,3,易见选S2为配置测点;第4次时,有效入度分别为:1,1,1,3,1,选取S4;最后,验证选取的4个测点的剩余实际入度分别为:5,5,4,5．所以使用改进贪婪算法的配置结果为Z={S2,S3,S4,S5}．

3应用举例

考虑如图3所示的卫星动量轮系统[3],经回路处理后的故障传播有向图如图4所示,其中S为可配置传感器的测点,F为故障源,测点与S8必须配置传感器．仅考虑系统相互独立的较大部分,并随机假设各测点传感器价格分别为250,300,350,300,350,150,350,400,200,200,150,300,300与350元．

图3　动量轮系统测点示意图Fig.3The selected points graph of the momentum wheel system

图4　动量轮系统的故障传播有向图Fig.4The fault propagation digraph of the momentum wheel system

对图4进行因果分析，可以看出F1与F2，F9,F10与F11所影响的测点集合完全相同，所以它们是不可分离的故障，为方便表示，将F1与F2合记为Ff，将F9,F10,F11合记为Fs.使用1.3的贪婪算法求取最小传感器配置方案，如表4所示，经过7次迭代，根据有效入度最大原则先后标记了S9,S10,S1,S8,S7,S12与S13后，二分图的根节点得到了完全的覆盖.但在删减之后的二分图中，S9的剩余实际入度已经变为0，这说明对于最小传感器配置集合，测点S9是

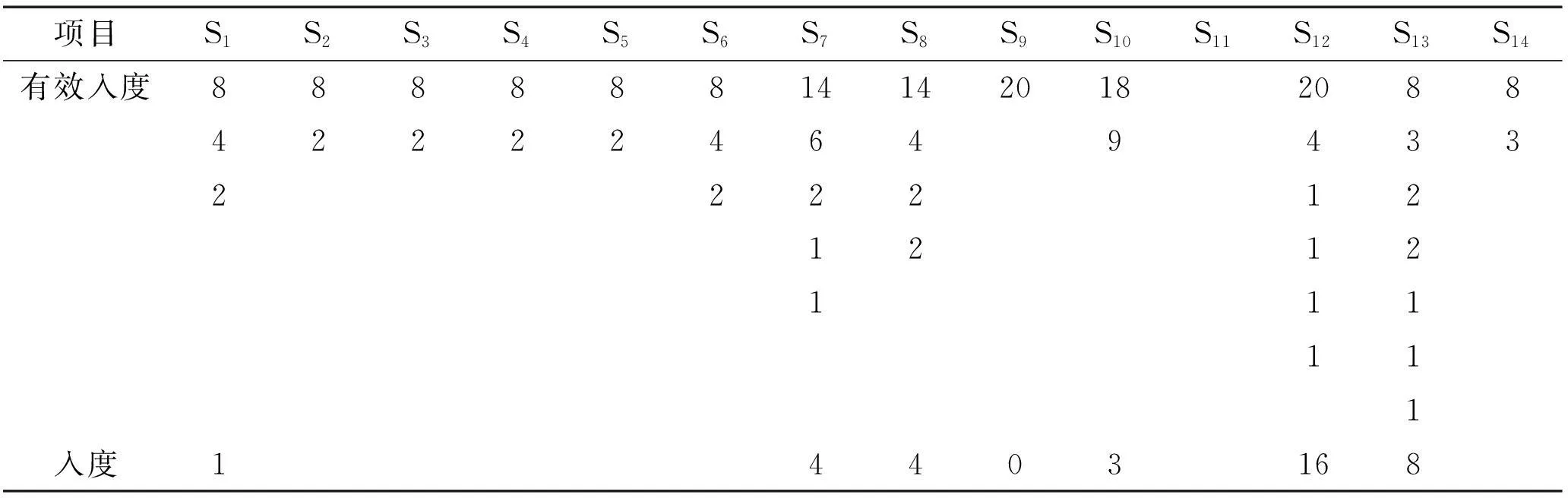
表4　动量轮系统迭代过程

一个冗余配置，其检测故障与分离故障的功能可以通过其他配置的测点加以实现，应将其从最小配置集合中除去.所以该动量轮系统满足故障可诊断的最小传感器配置为：{S1,S7,S8,S10,S12,S13}.

本文只考虑传感器的价格指标．根据文献[5],轴承温度遥测测点S5与电流控制器电流遥测测点S8在动量轮中是必须设置传感器的测点．因此本文在讨论最小代价配置问题时,人为的将上述两个测点所配置的传感器价格置为0．

根据表4,最小配置集合{S1,S7,S8,S10,S12,S13}包含6个传感器,其总成本为250+350+0+200+300+300=1 400,随机选取6个传感器的最小成本为800 (S11并没有用处)．记候选测点的总数为n=14-1-2=11,最少配置测点数为6,以传感器价格两两之差的最大公约数为步长，即h=50．搜寻得到的集合{S6,S7,S10,S12,S13},总价格相对最小配置少了100,为1 300,且满足了两个特定测点必须配置传感器的要求．

综上所述,{S5,S6,S7,S8,S10,S12,S13}为最小代价配置,实际总代价为1 850元．而由于系统存在大量必须配置传感器的基本测点,最小传感器配置的补偿配置达到极差情况,为{S1,S7,S8,S10,S12,S13}．

4结论

本文对于满足故障可诊断性的传感器优化配置问题,从系统的物理结构和数学模型出发,采用了有向图的定性方法．在不考虑个别部件的非线性特性的情况下,分析了故障的传播模式,以最小传感器配置方法为基础,给出了最小代价传感器配置方案与传感器故障补偿方案．但上述问题没有考虑系统不确定性对传感器优化配置的影响,还有待今后进一步的研究．

参考文献：

[1]彭涛．基于传感器最优配置的故障检测方法研究[D]．长沙:中南大学,2005:15-70.

[2]RAOR,MANIB,RAGHUNATHANR．Locatingsensorsincomplexchemicalplantsbasedonfaultdiagnosticobservabilitycriteria[J]．AicheJournal,1999,45(2):310-322.

[3]刘睿,周军,李鑫，等．基于DG的航天器部件可诊断性测点配置方法[J]．系统工程与电子技术,2014,36(10):2013-2017.

[4]COMMAULTC,DIONJM．Sensorlocationfordiagnosisinlinearstructuredsystemswithdisturbances[C]∥Proceedingsofthe42ndIEEEConferenceonDecisionandControl．Maui,USA:IEEE,2004:1443-1448.

[5]戴文战,陈杰．一种故障传播模型及故障源分离算法[J]．厦门大学学报(自然科学版),2001,40(S1):63-67.

[6]陈杰,戴文战．基于故障传递概率的故障源位置诊断方法[J]．厦门大学学报(自然科学版),2001，40(S1):58-62.

[7]AZAMM,PATTIPATIK,PATTERSON-HINEA．Optimalsensorallocationforfaultdetectionandisolation[C]∥Systems,ManandCybernetics,2004IEEEInternationalConferenceonIEEE.Hague,Netherland:IEEE,2004:1309-1314.

[8]ROSICHA,SARRATER,PUIGV,etal．Efficientoptimalsensorplacementformodel-basedFDIusinganincrementalalgorithm[C]∥Proceedingofthe46thIEEEConferenceonDecisionandControl．LosAngeles，USA:IEEE,2007:2590-2595.

[9]SARRATER,PUIGV,ESCOBETT,etal．Optimalsensorplacementformodel-basedfaultdetectionandisolation[C]∥Proceedingofthe46thIEEEConferenceonDecisionandControl.LosAngeles,USA:IEEE,2007:2584-2589.

[10]KRYSANDERM,ASLUNDJ,NYBERGM．Anefficientalgorithmforfindingminimaloverconstrainedsubsystemsformodel-baseddiagnosis[J]．IEEETransactionsonSystemsManandCyberneticsPartA:SystemsandHumans,2008,38(1):197-206.

[11]KRYSANDERM,FRISKE．Sensorplacementforfaultdiagnosis[J]．IEEETransactionsonSystemsManandCyberneticsPartA:SystemsandHumans,2008,38(6):1398-1410.

[12]刘文静,刘成瑞,王南华．基于可诊断性约束的测点优化配置研究[J]．空间控制技术与应用,2011,37(2):1-5.

Methods of Sensor Placement for Fault Diagnosis

LIU Lisang1,HU Xiaoqiang2,PENG Xiafu2*,WAN Binhao2

(1.College of Information Science and Engineering,Fujian University of Technology,Fuzhou 350118,China;2．School of Aerospace Engineering,Xiamen University,Xiamen 361005,China)

Abstract:Based on the directed graphs (DG),this paper investigates the method for optimizing the sensor configuration which can meet the fault diagnosability of nonlinear system described by component-level physical structure or a mathematical model．On one hand,a greedy algorithm satisfied failure detectability and separability is introduced particularly．Some discussions of the optimization method are made from two directions then．With the minimum configuration generated by the greedy algorithm as a starting point,a further searching algorithm in the principle of minimum cost which is considered as the hybrid of price,weight,volume and wastage makes the configuration of system sensors to be more realistic．On the other hand,in consideration of losses of failure diagnostic capability leaded by faulted sensor in minimum sensor configuration,this paper presents a compensated sensor configuration to all potential lost fault diagnostic functions and improves the greedy algorithm to achieve a direct compensation．Finally,the proposed approach is validated by using the momentum wheel system as an example.

Key words:sensor configuration;fault diagnostic;directed graph

doi：10.6043/j.issn.0438-0479.2016.03.022

收稿日期：2015-10-20录用日期：2016-02-18

基金项目：国家自然科学基金(61305117,61374037);国家重点实验室开放基金(9140c59030411ht05)

*通信作者：xfpeng@xmu.edu.cn

中图分类号:TP 274.5

文献标志码：A

文章编号：0438-0479(2016)03-0434-07

引文格式：刘丽桑，胡晓强，彭侠夫，等.满足故障可诊断性的传感器配置方法.厦门大学学报(自然科学版)，2016,55(3)：434-440.

Citation：LIU L S,HU X Q,PENG X F,et al．Methods of sensor placement for fault diagnosis.Journal of Xiamen University(Natural Science)，2016,55(3)：434-440．(in Chinese)