基于区域极点配置的挠性卫星姿态镇定控制

郑丹凤,周燕茹,曾建平

(厦门大学航空航天学院,福建厦门361005)

基于区域极点配置的挠性卫星姿态镇定控制

郑丹凤,周燕茹,曾建平

(厦门大学航空航天学院,福建厦门361005)

摘要：针对挠性卫星姿态系统,研究了基于区域极点配置的姿态镇定控制问题．通过对姿态系统进行近似线性化处理,并应用线性矩阵不等式(LMI)技术给出一种基于降维观测器的状态反馈控制方法．该方法根据分离原理,分别采用区域极点配置和极点配置定理设计控制器和观测器．对某挠性卫星模型进行数值仿真，并与一种非线性控制方法做比较研究．仿真结果表明该方法兼顾了卫星姿态系统的动态和稳态性能,且在小角度姿态镇定控制上具有显著优势．

关键词：挠性卫星;姿态控制;区域极点配置;观测器

现代卫星由于执行任务复杂,续航时间长,需要在其上安装太阳能电池板、液体箱等大型附件来满足能量需求．受运载能力限制,这些附件的质量应尽可能轻,一般选用低刚度的挠性材料制造．这造成了现代卫星具有挠性部件众多、动力学特征复杂、低频模态密集等特点,对高指向精度和高稳定度的卫星姿态控制带来极大挑战,是当前姿态控制领域的一个难点和热点问题[1-9]．近年来,挠性卫星姿态控制已取得了较多的研究成果．管萍等[4]提出了一种输入输出反馈线性化控制和自适应模糊滑模控制相结合的方法,在实现系统快速机动到期望值的同时有效抑制了挠性附件振动．宋斌等[5]研究了挠性卫星姿态鲁棒H∞控制问题,仿真结果表明所设计的控制器具有较强鲁棒性．周燕茹等[6]针对挠性卫星姿态机动和振动抑制问题,给出了一种基于多项式平方和(SOS)的非线性局部镇定控制方法．

当前航天工程应用中,挠性卫星姿态系统的控制设计仍以近似线性化方法为主,但传统的近似线性化设计方法,因各项性能指标易相互冲突,难以满足一些高精度和高稳定度的姿态控制要求．因此,本文给出了一种基于区域极点配置的挠性卫星姿态系统控制方法,以期在保证姿态系统定位精度的同时,具备较好的动态特性．此外,考虑到挠性模态测量的工程实现成本高,本文的姿态控制采用基于挠性模态观测器的状态反馈控制方案．通过对某挠性卫星姿态系统进行数值仿真研究,验证了所设计方法的可行性和有效性．

文中符号规定说明如下：In表示n维单位矩阵,Rn表示n维实向量空间,Rn×m表示n×m维实矩阵空间,A⊗B表示矩阵A和B的Kronecker乘积．假定所有矩阵具有合适维数．

1预备知识与问题描述

1.1预备知识

定义1[10]对复平面区域D,如果存在一个对称矩阵N∈Rm×m和矩阵M∈Rm×m，使得

定义2[10]对复平面给定的LMI区域D和矩阵A∈Rn×n,如果矩阵A的所有特征值都位于区域D中,则称矩阵A为D稳定的．

引理1[10]给定LMI区域D,矩阵A∈Rn×n是D稳定的充分必要条件是,存在一个对称正定矩阵P∈Rn×n,使得

MD(A,P)=N⊗P+M⊗(AP)+

MT⊗(AP)T<0．

1.2问题描述

考虑如下挠性卫星非线性姿态系统[6]:

(1)

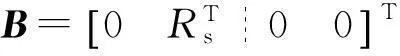
由于挠性卫星姿态系统中可直接测量的是状态xa,故系统输出方程为:

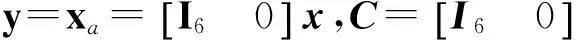
(2)

将挠性卫星非线性姿态系统(1)在零平衡点线性化,得到线性化系统模型为:

(3)

本文的控制目标是针对挠性卫星线性姿态系统(3),应用区域极点配置的方法设计出基于挠性模态观测器的状态反馈控制器,使得闭环系统在渐近稳定的同时满足一定的性能指标．

2基于区域极点配置的控制器设计

由于状态xb不可直接测量,为实现挠性卫星的姿态镇定控制,本文采用基于降维观测器的状态反馈控制设计方案．考虑如下降维观测器:

(4)

注1对系统(3),易验证(A22,A12)完全能观测,根据极点配置定理,可选取L使得(A22-LA12)的极点配置在任意位置．

基于降维观测器(4),设计状态反馈控制器:

(5)

其中K∈R3×n为控制器增益矩阵．相应闭环系统的整体结构图如图1所示.

图1　闭环系统Fig.1Closed-loop system

为实现本文控制目标,根据线性系统的分离原理，采用如下的区域极点配置方法设计状态反馈控制器(5),而降维观测器(4)则通过期望极点配置构造．

图2　区域D(α,r,θ)Fig.2Region D(α,r,θ)

为获得满意的动态性能,设计控制器使闭环极点配置在图2所示区域D(α,r,θ),可保证最小衰减率α,最小阻尼比ζ=cosθ和最大阻尼自然频率ωd=rsinθ,从而确保系统的最大超调量、衰减时间、上升时间和调节时间等过渡过程指标不超过由ζ、ωd确定的上界[10]．该区域可看成是一个半平面区域、一个圆盘和一个圆锥扇形这3个区域的交集．

下面给出挠性卫星线性姿态系统(3)在区域D(α,r,θ)极点配置的可解性条件．

定理1对于系统(3),若存在正定对称矩阵P和矩阵W,满足如下不等式约束：

2αP+AP+PAT+BW+WTBT<0，

(6)

(7)

(8)

其中,

Q11=APsinθ+P(Asinθ)T+(Bsinθ)W+

WT(Bsinθ)T,

Q12=APcosθ-PATcosθ+BWcosθ-

WTBTcosθ,

则存在一个控制器K=WP-1，可保证该状态反馈相应

闭环系统的极点配置在区域D(α,r,θ)．

证明令W=KP,H=(A+BK)P，则不等式约束(6)～(8)可转化为如下形式:

2αP+H+HT<0,

(9)

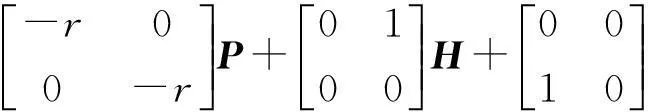
HT<0,

(10)

(11)

根据引理1,不等式(9)～(11)为该状态反馈相应的闭环系统矩阵(A+BK)在区域D(α,r,θ)稳定的条件．证毕．

3数值仿真

考虑某挠性卫星姿态系统[6],相关参数如下:

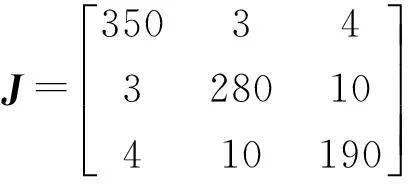
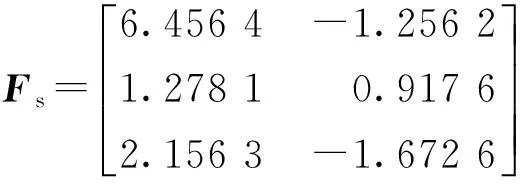
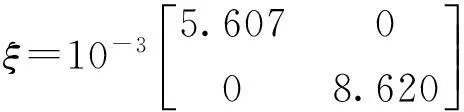
将上述参数代入系统(3),可得

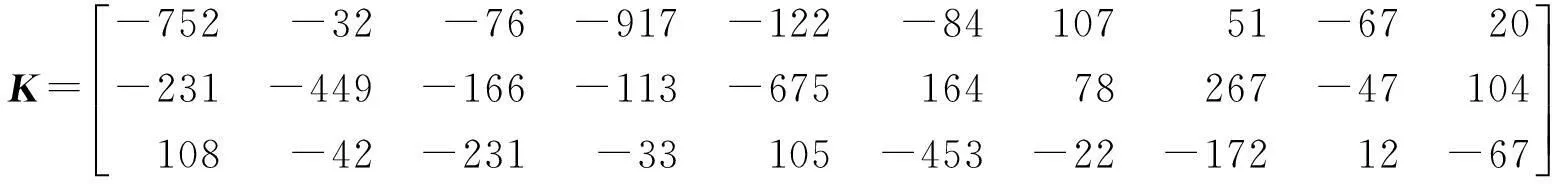
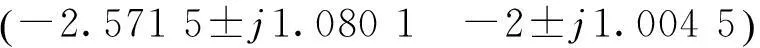
图3　11°姿态变化响应曲线Fig.3Response curves of 11° attitude variation

对比图3和4可看出,当卫星姿态转动角度增大时,本文线性控制的闭环响应调节时间和超调量分别增大．

对比图3～5可以看出,当转动角度不断增大时,本文线性控制的闭环响应有较大振荡,而文献[6]的非线性方法仍保持了良好的控制效果．

综上所述,当挠性卫星进行小角度姿态转动时,本文的线性控制实现的闭环响应速度快,超调量小,能够快速抑制由于姿态转动引起的挠性模态振动;当挠性卫星姿态转动角度增大时,线性控制的效果逐渐变差,而文献[6]的非线性方法依然保持良好的控制效果．

4结论

图4　50°姿态变化响应曲线Fig.4Response curves of 50° attitude variation

图5　103°姿态变化响应曲线Fig.5Response curves of 103° attitude variation

基于区域极点配置方法,本文研究了挠性卫星姿态镇定控制问题．通过对挠性卫星非线性姿态系统进行线性化处理,设计了一种基于降维观测器的状态反馈控制方法．根据线性系统的分离原理,分别采用区域极点配置和极点配置定理得出了状态控制器和观测器．最后,将该方法应用于某型挠性卫星并与一种非线性方法做比较研究,仿真结果表明文中方法在小角度姿态镇定控制问题上具有优势．

参考文献：

[1]KIDAT,YAMAGUCHII,CHIDAY,etal．On-orbitrobustcontrolexperimentofflexiblespacecraftETS-VI[J]．JournalofGuidance,Control,andDynamics,1997,20(5):865-872.

[2]HUQ,MAG．Variablestructurecontrolandactivevibrationsuppressionofflexiblespacecraftduringatti-tudemaneuver[J]．AerospaceScienceandTechnology,2005,9(4):307-317.

[3]PATELTR,KUMARKD,BEHDINANK．Variablestructurecontrolforsatelliteattitudestabilizationinellipticorbitsusingsolarradiationpressure[J]．ActaAstronautica,2009,64(2):359-373.

[4]管萍,刘小河,刘向杰．挠性卫星的变结构姿态控制[J]．控制理论与应用,2007,24(3):480-484.

[5]宋斌,马广畜,李传江,等．基于H∞鲁棒控制的挠性卫星姿态控制[J]．系统仿真学报,2005,17(4):968-970.

[6]周燕茹,黄文超,曾建平．挠性卫星姿态非线性局部镇定控制[J]．控制理论与应用,2014,31(3):279-284.

[7]DONGC,XUL,CHENY,etal．Networkedflexiblespacecraftattitudemaneuverbasedonadaptivefuzzyslidingmodecontrol[J]．ActaAstronautica,2009,65(11):1561-1570.

[8]胡庆雷,刘亚秋,马广富．挠性航天器姿态机动的变结构主动振动抑制[J]．控制理论与应用,2007,24(3):329-336.

[9]耿云海,吴炜平,马玉海．神经网络补偿的挠性卫星敏捷姿态机动[J]．哈尔滨工业大学学报,2012,44(5):31-35.

[10]俞立．鲁棒控制——线性矩阵不等式处理方法[M]．北京:清华大学出版社,2002:96-104.

Flexible Satellite Attitude Stabilization Control Based on Regional Pole Assignment

ZHENG Danfeng,ZHOU Yanru,ZENG Jianping*

(School of Aerospace Engineering,Xiamen University,Xiamen 361005,China)

Abstract:Based on regional-pole assignment,the attitude stabilization control problem is studied for the flexible satellite-attitude system．Through the approximate linearization of the attitude system and linear matrix inequality (LMI) technique,a state feedback control approach based on the reduced-order observer is provided．According to the separation principle,the controller and the observer are obtained by regional pole assignment and theorem of pole assignment,respectively．Finally,the method is validated over the nonlinear model of a flexible satellite．Simulation results show that,compared with a nonlinear control approach,the proposed method guarantees both dynamic and steady state performances of the satellite attitude system．Furthermore,the method enjoys significant advantages in small angle attitude stabilization control.

Key words:flexible satellite;attitude control;regional pole assignment;observer

doi：10.6043/j.issn.0438-0479.2016.03.013

收稿日期：2015-09-15录用日期：2015-12-21

基金项目：国家自然科学基金(61374037);中央高校基本科研业务费专项(20720150177)

*通信作者：jpzeng@xmu.edu.cn

中图分类号:V 448.22

文献标志码：A

文章编号：0438-0479(2016)03-0376-06

引文格式：郑丹凤,周燕茹,曾建平.基于区域极点配置的挠性卫星姿态镇定控制.厦门大学学报(自然科学版)，2016,55(3)：376-381.

Citation：ZHENG D F,ZHOU Y R,ZENG J P．Flexible satellite attitude stabilization control based on regional-pole assignment.Journal of Xiamen University(Natural Science)，2016,55(3)：376-381．(in Chinese)