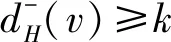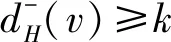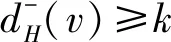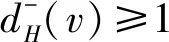有向图的Roman k-控制
2021-06-24张晓转
张晓转, 孟 巍
(山西大学 数学科学学院,山西 太原 030006)
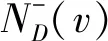
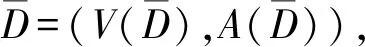
设S是有向图D的顶点集V的一个子集,如果N+[S]=V,则称S是有向图D的一个控制集[1].有向图D中最小控制集的阶称为D的控制数,记作γ(D)[1].设k是一个正整数,S是有向图D中V的一个顶点子集,如果|N-(v)∩S|≥k对于每个v∈VS均成立,则称S是有向图D中的一个k-控制集.有向图D中最小k-控制集的阶称为k-控制数,记作γk(D).有向图D中的一个阶数最小的k-控制集叫做γk(D)-集.有向图D中的一个阶数最小的1-控制集叫做γ(D)-集.
图的控制参数是图的一个重要参数,它与染色体,划分数等其他参数有着密切的联系,并且它与组合优化,理论计算机科学等其他学科领域都有着密切的联系.基于不同的实际背景,图论研究者在图的控制理论的基础上定义了许多图的控制参数,比如图的符号控制,图的k-距离控制,图的Roman控制等.2004年,Cockayne[2]等给出了无向图的Roman控制函数的定义及其相关结论.后来,Lutz[1]将它推广到了有向图中,给出了有向图的Roman控制函数.称函数f:V→{0,1,2}为有向图D的一个Roman控制函数,如果对于每个f(v)=0的顶点v都至少有一个入邻点w满足f(w)=2.Roman控制函数f权值是指在函数f作用下各个顶点的值的和,即ω(f)=∑v∈Vf(v).有向图D的权值最小的Roman控制函数的权值称作有向图D的Roman控制数,记作γR(D).如果函数f是Roman控制函数并且ω(f)=γR(D),则称f是γR(D)-函数.
Kammerling和Volkmann[3]推广了无向图的Roman控制函数,得到了无向图的罗马Romank-控制函数并且给出了关于无向图的Romank-控制函数的大量结果.设k是一个正整数,称函数f:V→{0,1,2}是无向图G的一个Romank-控制函数,如果对于每个f(v)=0的顶点v都至少有k个邻点v1,v2,…,vk满足f(v1)=f(v2)=…=f(vk)=2.文中将这个函数推广到有向图中,对有向图的Romank-控制函数进行了定义和研究.设k是一个正整数,称函数f:V→{0,1,2}是有向图D的一个Romank-控制函数,如果对于每个f(v)=0的顶点v它都至少有k个入邻点v1,v2,…,vk满足f(v1)=f(v2)=…f(vk)=2.Romank-控制函数f的权值是在函数f作用下各个顶点的值的和,即ω(f)=∑v∈Vf(v).有向图D的权值最小的Romank-控制函数的权值称作是有向图D的Romank-控制数,记作γ{Rk}(D).显然,γ{Rk}(D)≤|V(D)|.如果函数f是D的Romank-控制函数且ω(f)=γ{Rk}(D),则称f是γ{Rk}(D)-函数.注意到Roman 1-控制数是Roman控制数.
设f是有向图D的一个Romank-控制函数,则f与V的有序划分(V0,V1,V2)是一一对应的,其中Vi={v∈V|f(v)=i},i=0,1,2.因此,以后可以记f=(V0,V1,V2).
Kammerling和Volkmann在文献[3]中给出了无向图的Roman k-控制数的一些性质.我们对这些性质进行了推广,首先给出了有向图中Roman k-控制数的一些性质,然后给出了一些特殊有向图的Roman k-控制数的界.
1 Roman k-控制数的一些性质
称有向图D是一个k-Roman有向图,如果γ{Rk}(D)=2γk(D).设S是有向图D的顶点集V的一个子集,称顶点v∈S关于集合S有一个副出邻点w,如果w∈N+(v)∩(VS)且N-(v)∩S={w}.
命题1γk(D)≤γ{Rk}(D)≤2γk(D).
证明设f=(V0,V1,V2)是有向图D的一个γ{Rk}(D)-函数,则V1∪V2是D的一个k-控制集,从而γk(D)≤|V1|+|V2|≤|V1|+2|V2|=γ{Rk}(D).
设S是有向图D的一个γk(D)-集,则f=(VS,∅,S)是D的一个Romank-控制函数,因此γ{Rk}(D)≤2|S|≤2γk(D),证毕.
推论[1]γ(D)≤γR(D)≤2γ(D).
命题2一个有向图D是k-Roman有向图当且仅当它有一个γ{Rk}(D)-函数f=(V0,V1,V2)满足V1=∅.
证明如果D是k-Roman有向图,设S是有向图D的一个γk(D)-集,则f=(VS,∅,S)是D的一个Romank-控制函数且ω(f)=2|S|=2γk(D)=γ{Rk}(D).所以D有一个γ{Rk}(D)-函数f=(V0,V1,V2)满足V1=∅.
反之,如果D有一个γ{Rk}(D)-函数f=(V0,V1,V2)满足V1=∅,那么γ{Rk}(D)=2|V2|,并且|V2|是D的一个k-控制集.因此2γk(D)≤2|V2|=γ{Rk}(D).结合命题1得γ{Rk}(D)=2γk(D),因此D是k-Roman罗马有向图,证毕.
推论[1]一个有向图D是1-Roman有向图当且仅当它有一个γR(D)-函数f=(V0,V1,V2)满足V1=∅.
命题3设D是一个n阶有向图,则以下3条等价:
1)γk(D)=γ{Rk}(D);
2)γk(D)=n;
3) Δ-(D)≤k-1.
证明首先由1)证2).设f=(V0,V1,V2)是有向图D的一个γ{Rk}(D)-函数,由于γ{Rk}(D)=γk(D)≤|V1|+|V2|≤|V1|+2|V2|=γ{Rk}(D),可得|V0|=|V2|=0,因此γk(D)=γ{Rk}(D)=n,2)得证.
下一步由2)证3).如果存在一个顶点v∈V(D)使得d-(v)≥k,则V{v}是D的一个k-控制集.因此,γk(D)≤n-1,矛盾! 故3)成立.
最后由3)证1).由Δ-(D)≤k-1,可得γk(D)=n.由于γ{Rk}(D)≤n=γk(D),结合命题1可知1)成立.
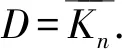
命题4设f=(V0,V1,V2)是有向图D的任意一个γ{Rk}(D)-函数,则以下结论成立:
1)D[V1]不包含这样的二部子图: 它有一个二划分(X,Y)满足X中的每个顶点和Y中的任何一个顶点形成一条弧,且以X中的顶点为尾和Y中的顶点为头,其中
|Y|=k+1;
2) 如果w∈V1,则|N-(w)∩V2|≤k-1;
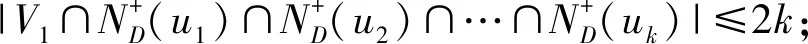
4)V2是D的导出子图D[V0∪V2]的一个γk-集;

证明1) 假设D[V1]包含一个符合题中条件的有向二部子图,则f′=(V0∪Y,V1-(X∪Y),V2∪X)也是有向图D的一个Romank-控制函数,并且它的权值
ω(f′)=|V1-(X∪Y)|+2|V2∪X| =|V1|+2|V2|+|X|-|Y| =|V1|+2|V2|-1 =ω(f)-1.
这与f是有向图D的一个γ{Rk}(D)-函数矛盾,因而1)得证.
2) 假设|N-(w)∩V2|≥k,则f′=(V0∪{w},V1{w},V2)也是有向图D的一个Romank-控制函数,并且ω(f′)=ω(f)-1.这与f是有向图D的一个γ{Rk}(D)-函数矛盾,因而2)得证.

ω(f′)=|V1-B|+2|V2∪A|=|V1|+2|V2|+2|A|-|B|=|V1|+2|V2|-1=ω(f)-1.
这与f是有向图D的一个γ{Rk}(D)-函数矛盾,因而3)得证.
4) 由f=(V0,V1,V2)是有向图D的任意一个Romank-控制函数的定义可得结论.
5) 首先可知v有一个出邻点在V0中,否则f′=(V0,V1∪{v},V2-{v})也是D的一个Romank-控制函数,并且它的权值ω(f′)=ω(f)-1,这与f是有向图D的一个γ{Rk}(D)-函数矛盾.
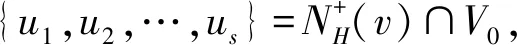
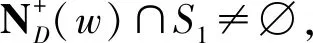
推论[1]设f=(V0,V1,V2)是有向图D的任意一个γR(D)-函数,则以下结论成立:
1) Δ+(D[V1])≤1;
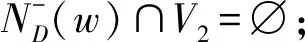
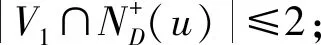
4)V2是导出子图D[V0∪V2]的一个γ-集;
5) 设H=D[V0∪V2],则在V2中每个满足N-(v)∩V2≠∅的顶点v至少有2个关于V2的副出邻点在H中.
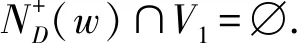

ω(f′)=|V1-{y}|+2|(V2-{v})∪{w}|=|V1|+2|V2|-1=ω(f)-1.
这与f是有向图D的任意一个γR(D)-函数矛盾,证毕.
2 Roman k-控制数
首先,命题5给出了在一般情况下Romank-控制数的界; 然后,命题6、7、8给出了在一些限定条件下Romank-控制数的界; 最后给出了有向路和有向圈的Romank-控制数的值.分别记Pn和Cn为n阶有向路和n阶有向圈.
命题5设D是一个n阶有向图,则γ{Rk}(D)≥min{n,γk(D)+k}.
证明显然γ{Rk}(D)≤n.如果γ{Rk}(D)=n,证毕.如果γ{Rk}(D) |V1|+2|V2|=γ{Rk}(D)≤γk(D)+k-1≤|V1|+|V2|+k-1. 计算可得|V2|≤k-1.结合f=(V0,V1,V2)是有向图D的一个γ{Rk}(D)-函数知|V0|=|V2|=0,所以γ{Rk}(D)=|V1|=n,这与假设γ{Rk}(D) 推论[1]设D是一个n阶有向图,则γR(D)≥min{n,γ(D)+1}. 命题6设D是一个n阶有向图,则下列结论成立: 1) 如果n≤2k,则γ{Rk}(D)=n; 2) 如果n≥2k+1,则γ{Rk}(D)≥2k; 3) 如果n≤2k+1,并且γk(D)=k,则γ{Rk}(D)=2k. 证明设f=(V0,V1,V2)是有向图D的一个γ{Rk}(D)-函数.显然γ{Rk}(D)≤n. 1) 假设γ{Rk}(D) 2) 如果γ{Rk}(D)=n,因为n≥2k+1,所以γ{Rk}(D)≥2k,证毕.如果γ{Rk}(D) 3) 设S是D的一个γk(D)-集,则f=(VS,∅,S)是D的一个Romank-控制函数,因此γ{Rk}(D)≤2|S|=2k,结合2)可知γ{Rk}(D)=2k,证毕. 给定一个有向图D,如果顶点集V中仅有一个顶点v∈V的入度为0,且剩余任意顶点w∈V{v}与该顶点都存在(v,w)-路,则D叫做有向出树,其中v叫做有向出树的根,出度为0的顶点叫做有向出树的叶子.有向星图是仅有一个顶点不是叶子的有向出树. 推论设D是一个n≥3阶有向星图,则γR(D)=2. γ{Rk}(D)≤|V-(X∪Y)|+2|Y|=n-|X|+|Y| 命题8设D是一个n阶有向图,并且D的最大出度Δ+(D)≥k,则γ{Rk}(D)≥2n(Δ+/k+1). 证明设f=(V0,V1,V2)是一个γ{Rk}(D)-函数.因为V0的每个顶点至少有k个入邻点在V2中,所以k|V0|≤Δ+|V2|,进而可得 (Δ+/k+1)γ{Rk}(D)=(Δ+/k+1)(|V1|+2|V2|)=(Δ+/k+1)|V1|+2(Δ+/k+1)|V2|≥ (Δ+/k+1)|V1|+2|V0|+2|V2|≥2|V1|+2|V0|+2|V2|=2n. 证毕. 推论Ⅰ设D是一个n阶有向图,并且D的最大出度Δ+(D)=k,则γ{Rk}(D)=n. 推论Ⅱ设D是一个n阶有向图,并且D的最大出度Δ+(D)=1,则γR(D)=n. 有向路和有向圈的最大出度Δ+(D)=1,由推论Ⅱ可知它们的Roman控制数的值.在下面的命题中给出它们的Romank-控制数的值. 命题9γ{Rk}(Pn)=γ{Rk}(Cn)=n. 证明下面只需证明γ{Rk}(Pn)=n,γ{Rk}(Cn)=n可类似证明. 设f是γ{Rk}(Pn)-函数,对于每个满足条件f(v)=0的顶点v,它至少有k个满足条件 f(w)=2的入邻点w.由于Pn是有向路,则其中每个顶点最多有一个入邻点.因此分下面2种情况讨论: 当k≥2时,每个顶点v满足f(v)=1,因此γ{Rk}(Pn)=n; 当k=1时,由推论Ⅱ可证.