本原有向图的scrambling指数和m-competition指数

方 炜，高玉斌

（1.中北大学 仪器与电子学院，山西 太原030051；2.中北大学 理学院，山西 太原030051）

0 引 言

令D=（V，E）是一个有向图，其点集V=V（D），边集E=E（D）.可以有环但是不能有重弧.用Cp来表示一个长度为p的圈.一个有向图D是本原的，当且仅当存在正整数k，使得D中的任意一点x到另外一点y（y可能等于x）都存在k长途径.这样的最小的正整数k就是有向图D的本原指数，用exp（D）表示.

在2009年，Akelbek和Kirkland［1］共同提出了本原有向图scrambling的指数这一概念.在本原有向图D中，如果对于任意一对顶点u，v，都能在D中找到一个顶点w并且u，v经过k长途径都能到达w，满足这样条件的最小的正整数k就称为本原有向图D的scrambling指数，用k（D）表示.

在2010年，Hwa Kyung Kim［2］提出了本原有向图m-competition指数的概念，在本原有向图D中，如果对于任意一对顶点u，v，都能在D中找到一个顶点集合V1=u1，v2，…，um-1，um，|V1|=m，并且u，v经过k长途径都能到达顶点集合V1，满足这样条件的最小的正整数k就称为D的mcompetition指数，用km（D）表示.其实m-competition指数是一种广义的scrambling指数.

对于n阶本原有向图D，通过本原指数，scrambling指数和m-competition指数的概念，可以这样的关系：k（D）=k1（D）≤k2（D）≤…≤kn（D）=exp（D）.

近年来，国内外很多专家对本原有向图的scrambling指数和m-competition指数进行了研究，如文献［3-15］.在文献［3］中，作者找到了本原有向图scrambling指数的上界，并找了取得上界的极图；在文献［4］中，作者研究了对称本原有向图的scrambling指数；在文献［5］中，作者研究了仅含两个圈的本原有向图scrambling指数；在文献［6］中，作者研究了本原对称含环有向图的m-competition指数.本文研究了一类含三个圈的本原有向图的srambling指数和一类仅含两个圈的本原有向图的m-competition指数.

1 主要结论

为了表达方便，用|Rt｛x｝|表示顶点x在D中经过t长途径所到达的顶点个数.令点集V1⊆V，用RV1t｛x｝表示顶点x经过t长途径到达V1中的点集，即RV1t｛x｝=Rt｛x｝∩V1.设D为n阶本原有向图，vi，vj∈V（D），如果在D中，vi经过t（t为正整数）长途径能到达vj，那么在有向图Dt中，vi只需经过1长途径就能到达vj.

定理1 设D1为如图1所示的n阶本原有向图，

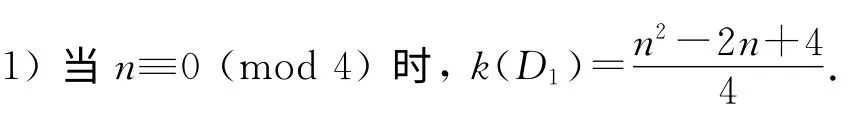
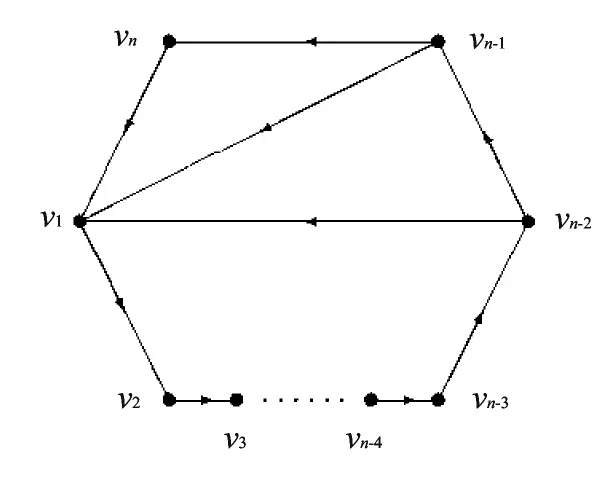
图1 D1 Fig.1 D1

证明 令vi，vj∈V（D1），如果在本原有向图D1中，vi经过n-2长途径能到达vj，那么在本原有向图Dn-21中，vi经过1长途径能到达vj.由本原有向图D1，可以得到Dn-21，如图2所示：

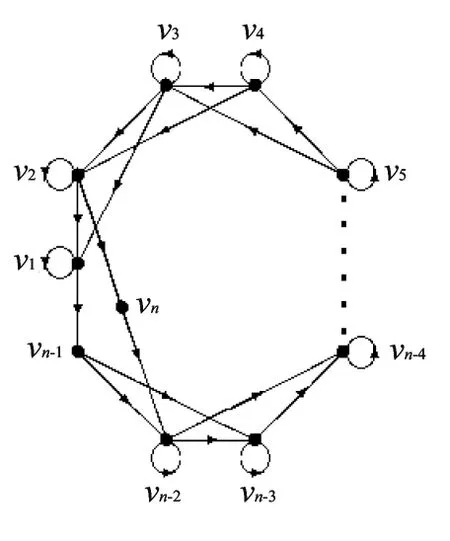
图2 Dn1-2 Fig.2 Dn1-2

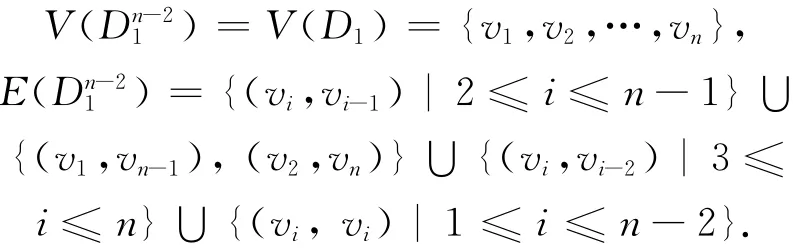
1）当n≡0（mod 4）时，在Dn-21中

因此在Dn-21中同时 对于顶点有同时在本原有向图D1中，对于任意的顶点vi，vj∈V（D1），vi，vj经过1长途径都至少能到达顶点集合｛v1，v2，…，vn-2｝中 的 一 个 点，所 以

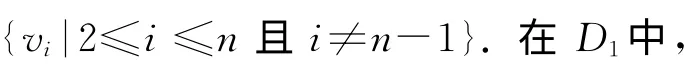
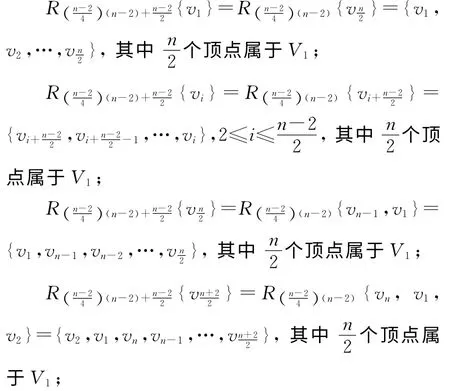
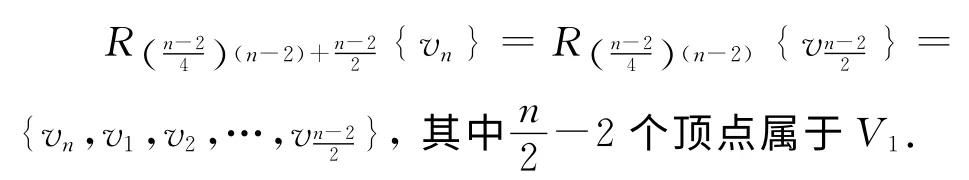
情况1 1≤i，j≤n-1.因为|V1|=n-2，所以对于任意的顶点

情况2 1≤i≤n-1，j=n.

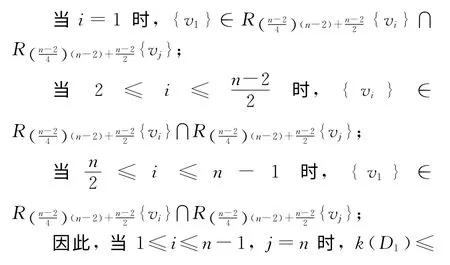
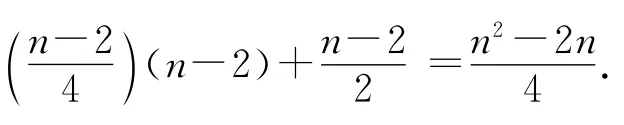
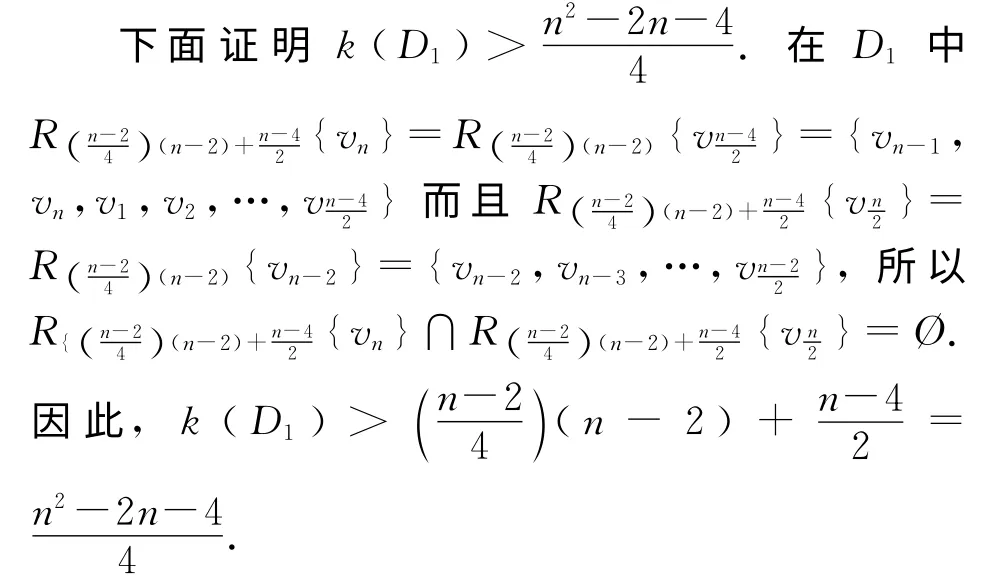
4）当n≡3（mod 4）时，

在D1中，当时，且同 时，其中有个点属于V2.

定理2 设D2为n阶有向图，如图3所示，D2含有1个n-3长圈和1个n-4长圈.

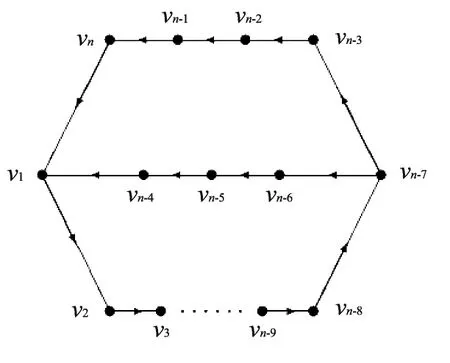
图3 D2 Fig.3 D 2

证明 令vi，vj∈V（D2），如果在本原有向图D2中，vi经过n-4长途径能到达vj，那么在本原有向图Dn-41中，vi经过1长途径能到达vj.如果在本原有向图D2中，vi经过n-3长途径能到达vj，那么在本原有向图Dn-31中，vi经过1长途径能到达vj.

由本原有向图D2，可以得到Dn-42，如图4所示：

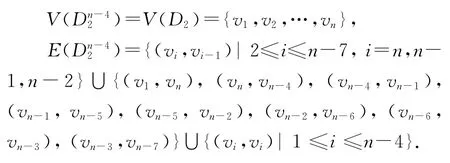
也可以得到Dn-32，如图5所示：

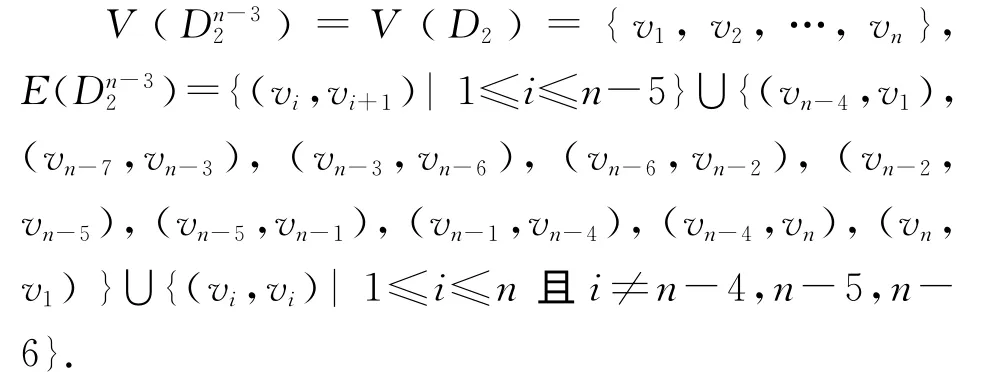
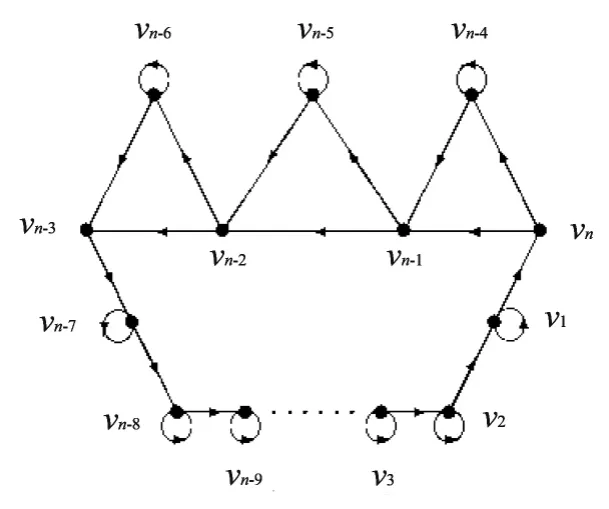
图4 Dn-42 Fig.4 Dn-42

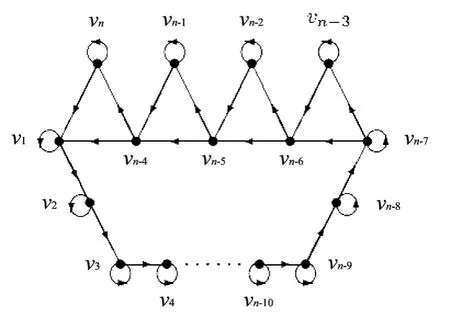
图5 Dn-32 Fig.5 Dn-32

1）当n+m为奇数时，在Dn-42中，令因为是 环 点，所 以其中在D2中，点集中的任意一个顶点经过4长途径都能到达而且

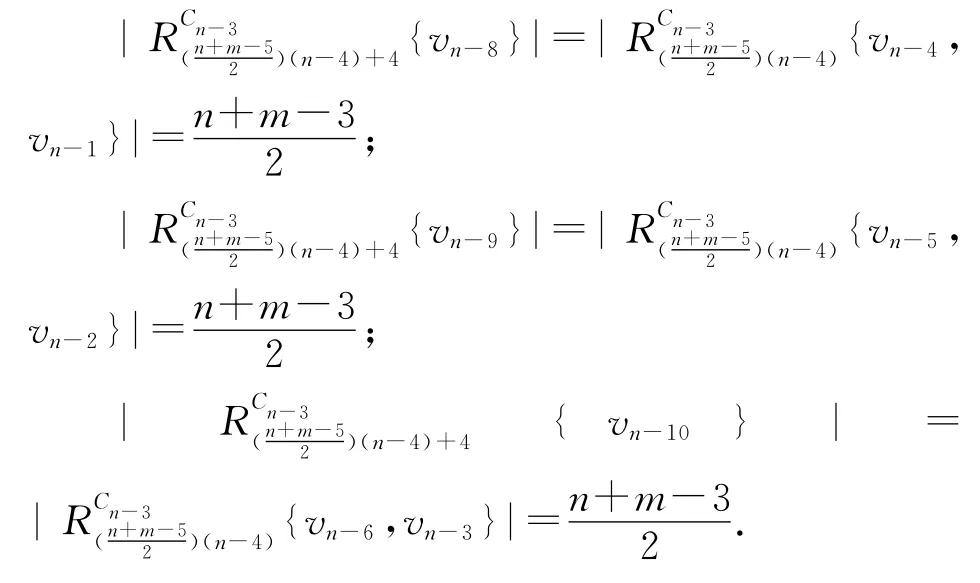
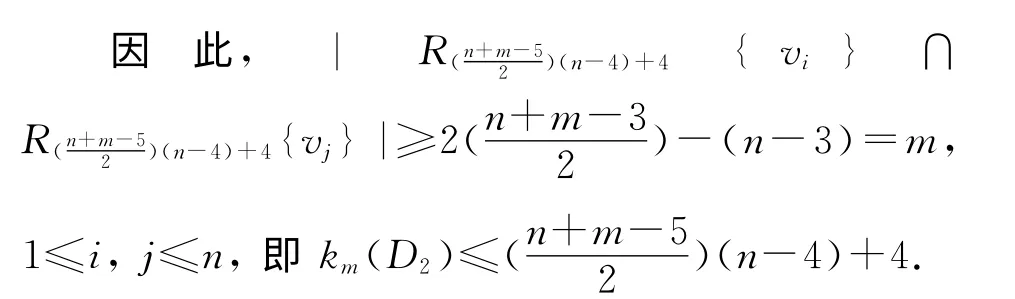
在本原有向图D2中，

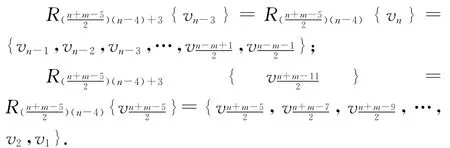
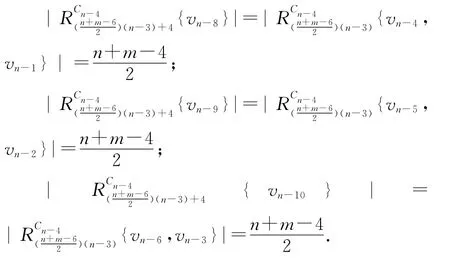
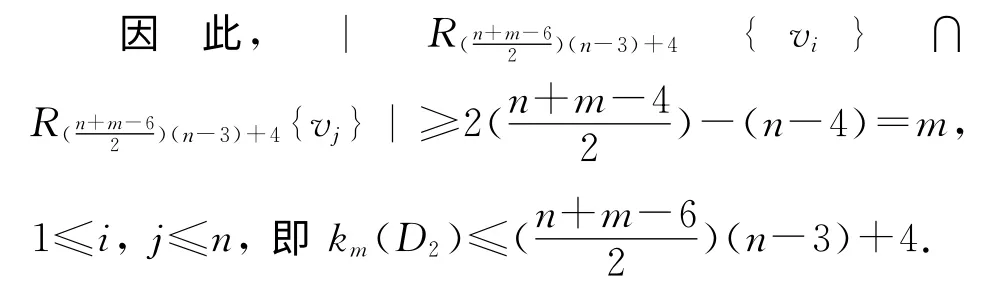
［1］Akelbek M，Kirkland S.Coefficients of ergodicity and the scrambling index［J］.Linear Algebra Appl.，2009，430（4）：1111-1130.

［2］Kim H K.Generalized competition index of a primitive digraph［J］.Linear Algebra and its Appl.，2010，433（1）：72-79.

［3］Akelbek M，Kirkland S.Primitive digraphs with the largest scrambling index［J］.Linear Algebra Appl.，2009，430（4）：1099-1110.

［4］Chen Shexi，Liu Bolian.The scrambling index of symmetric primitive matrices［J］.Linear Algebra and its Applications，2010，433（6）：1110-1126.

［5］Shao Yanling，Gao Yubin.The scrambling indices of primitive digraphs with exactly two cycles［J］.Ars Combination，2013，108：505-513.

［6］Shao Yanling，Gao Yubin.The m-competition indices of symmetric primitive digraphs with loop［J］.Ars Combination，2013，108：217-223.

［7］Kim H K，Lee S H.Generalized competition indices of symmetric primitive digraphs［J］.Discrete Applied Mathematics，2012，160（10-11）：1583-1590.

［8］Liu Bolian，Huang Yufei.The scrambling index of primitive digraphs［J］.Computers and Mathematics with Applications，2010，60（3）：706-721.

［9］Cho H H，Kim S R，Nam Y S.The m-step competition graph of a digraph［J］.Discrete Applied Mathematics，2010，105（1-3）：115-127.

［10］Kim H K.A bound on the generalized competition index of a primitive matrix using boolean rank［J］.Linear Algebra and Its Application，2011，435（9）：2166-2174.

［11］Kim H K，Park S G.Generalized competition indices of symmetric primitive digraphs［J］.Linear Algebra and Its Application，2012，436（1）：86-98.

［12］Kim H K.Generalized competition index of an irreducible boolean matrix［J］.Linear Algebra and Its Application，2013，438（6）：2747-2756.

［13］Kim H K.Scrambling index set of primitive digraphs［J］.Linear Algebra and Its Application，2013，439（7）：1886-1893.

［14］Shao Yanling，Gao Yubin，Li Zhongshan.The mcompetition indices of symmetric primitive digraphs without loops［J］.Electronic Journal of Linear Algebra，2012，23：457-472.

［15］Shao Yanling，Gao Yubin，Li Zhongshan.On the second largest scrambling index of primitive matrices［J］.Ars Combination，2014，113：457-462.