关于超欧拉的幂有向图

崔秋月，刘 娟

(新疆师范大学，新疆 乌鲁木齐 830017)

关于超欧拉的幂有向图

崔秋月，刘 娟*

(新疆师范大学，新疆 乌鲁木齐 830017)

如果一个有向图D包含一个生成有向闭迹，则称D是超欧拉有向图。研究关于一个强连通有向图或一个强连通的有向图类，使之在经过p次幂有向图的运算后成为超欧拉有向图的充分条件：有向图D包含一个有向圈的集合 Γ=｛S1，S1，…，Sn｝且满足 V（D）=Usi∈ΓV(Si)，D 的平方图是超欧拉有向图的充分条件。对于s,t图类中的强连通有向图，当s是奇数时，则对于任意的是超欧拉有向图；当s是偶数时，则对于任意的是超欧拉有向图。

超欧拉有向图；p次幂有向图；平方图；欧拉有向图

1 预备知识

本文只考虑没有自环 (一条弧的两个端点为同一个点)和平行弧(两个点之间有两条方向相同的弧)的简单有向图。没有被定义的术语和符号在文献[1]中可以参考。令 D=（V（D），A（D））是简单有向图,其中有向图D的点集为V（D），弧集为A（D）。在本文中，我们用符号（u，v）表示有向图中从点u到点v的一条弧。对于一个整数 n，定义［n］=｛1，2，…，n｝。有向图D中的一个道是一个交替序列W=x1a1x2a2x3…xk-1ak-1xk，其中 xi为点，aj为弧使得 aj=（xj，xj+1）,对于每一个 i∈[k]，j∈[k-1]，则称 W 是一个从 x1到 xk的道或者是一个（x1，xk）-道。如果 x1=xk，则称 W 是一个闭道，否则是开道。当W的弧在文章中已被理解时，可以记W为x1x2…xk。如果x1≠xk，则点x1是W的起点，点xk是W的终点，x1和xk是W的端点。道的长度是它的弧的条数。有向图D中的一个有向迹是一个所有弧都不同的道；一个有向路是一个所有点都不同的道。如果 W 中 x1，x2，…，xk-1是不同的点，k≥2且x1=xk，则称W是一个有向圈。如果对于有向图D中每对不同的点x，y都存在一个（x，y）-道和一个（y，x）-道,则称 D 是强连通的。令 W=x1x2…xk，Q=y1y2…yt是有向图D中的一对道，如果V（W）∩V（Q）= ∅ ，则称W和Q是点不交的；如果A（W）∩A（Q）= ∅ ，则称W和Q是弧不交的。如果V（H）⊆ V（D），A（H）⊆A（D）并且A（H）中的每一条弧的两个端点都在V（H）中，则称H是D的一个子图。如果V（H）=V（D），则 称H是D的一个生成子图。如果A（D）中每一条弧都在A（H）中，每一条弧的两个端点都在V（H）中，则称 H 是由 X=V（H）诱导的，记作 H=D〈X〉并称H是D的一个诱导子图。如果H是D的一个子图且 S ⊆ A（D）-A（H），V（D〈S〉）⊆ V（H），则称H+S是D的子图，其点集为V（H），弧集为A（H）+S。我们一般用D-a代替 D-｛a｝，用 D+a代替 D+｛a｝。令D1和D2是两个不交的有向图，D1与D2的并记作D1∪D2，它的点集为 V（D1∪D2）=V（D1）∪V（D2）,弧集为 A（D1∪D2）=A（D1）∪A（D2）。对于 X，Y ⊆ V（D），定义（X，Y）D=｛（x，y）∈A（D）：x∈X，y∈Y｝。当 Y=V（D）-X 时，定义 ∂+D（ X）=（X，V（D）-X）D和 ∂−（DX）=（V（D）-X，X）D。对于一个点 v∈V（D），是D中点v的出度，是D中点v的入度。如果x，y是D中的两个点且x到y是可达的,则在D中从x到y的距离记作dis（tx，y），是（x，y）-道的最小长度,否则dis（tx，y）=∞。D中的一个点集X到另一个点集Y的距离为dis（tX，Y）=max｛dis（tx，y），x∈X，y∈Y｝。有向图D的直径为diam（D）=dis（tV，V），即diam（D）=max｛dis（tV，V），x∈V，y∈V｝。我们定义,如果有向图D中只有一个点，则diam（D）=0。如果D不是强连通有向图，即存在两个点x，y使得dis（tx，y）=∞，则diam（x，y）=∞。如果对于有向图D中任意一对不同的点 x，y，既存在（x，y），又存在(y，x)，则称D为完全有向图。

下面介绍p次幂有向图的定义。

定义1[1]对于一个正整数p和一个有向图D，p次幂有向图 D 定义如下:V（D ）=V（D）,如果x≠y且有dis（tx，y）≤p，则有（x，y）∈A（D）。

根据以上的定义易知D1=D。当p=2时,称D2为D的平方图。当p=3时，称D3为D的立方图。

如果D不是强连通有向图,则p次幂有向图不是强连通的且不可能包含一个生成闭有向迹。因此，以下所有的有向图都假设是强连通的。

Boesch，Suffel和 Tindell[2]在 1977 年提出了超欧拉问题,他们致力于刻画出包含生成欧拉子图的无向图，同时他们表示这个问题是非常困难的。Pulleyblank[3]在1979年证明了判定一个无向图(甚至包含平面无向图)是否是超欧拉的是NP-complete。截至今日，已经有大量关于超欧拉无向图的研究，例如文献[4-6]。

因此，在超欧拉无向图的基础上，超欧拉有向图很快便被广泛的研究。如果一个有向图D包含一个有向闭迹W使得A（W）=A（D），则称D是欧拉有向图。如果一个有向图D包含一个有向闭迹W使得V（W）=V（D）或包含一个生成欧拉子图,则称D是超欧拉有向图。否则，称D是非超欧拉有向图。如今,最主要的问题就是判定一个有向图是超欧拉有向图。Gutin[7，8]进行了早期的研究。一些近期的发展可以参考文献[9，10]。

2 主要结果

命题1[1]一个有向图D的直径是有限的当且仅当D是强连通的。

定理1 设D是一个强连通有向图且diam（D）=d，则D的d次幂有向图是完全有向图。

证明 设 V（D）=｛v1，v2，…，vn｝并且对于 D 中的任意两个不同的点 vi和 vj，i≠j且 i，j∈[n]。根据 p次幂有向图的定义,可以得出V（Dd）=V(D)。因为D是一个强连通有向图且diam（D）=d，则D中有dist（vi，vj）≤diam(D)=d，所以对于有向图Dd中任意两个不同的点vi和vj都存在（vi，vj）和(vj，vi)，因此，有向图Dd是完全有向图。

定理 2 设 Γ=｛S1，S2，…，Sn｝是有向图 D 中的有向圈的集合并且V（D）=Usi∈ΓV（Si）。如果满足对任意的1≤i≤n，1≤j≤n+1，│（Si，Sj）D│=1当且仅当j=i+1，j是以n为模的,则D的平方图是超欧拉有向图。

证明 我们想要在D的平方图中构造一个生成有向闭迹S。因为│（Si，Sj）D│=1当且仅当j=i+1，j是以 n为模的，1≤i≤n，1≤j≤n+1，所以任意的 Si中存在一个点的出度为2，一个点的入度为2，不妨假设即D中存在弧设任意的其中

下面讨论w的奇偶性:

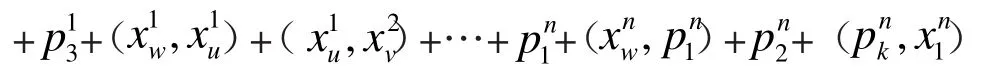
定理 3 设 Γ=｛S1，S2，…，Sn｝是有向图 D 中的有向圈的集合并且V（D）=Usi∈ΓV（S）i。如果满足对任意的 1≤i＜j≤n，Si和 Sj恰有一段公共弧且只存在于Si和Sj中当且仅当j=i+1，则D的平方图是超欧拉有向图。

证明 因为 Γ=｛S1，S2，…，Sn｝是 D 中的有向圈的集合且满足V（D）=Usi∈ΓV（S）i，所以，如果n=1，则D是超欧拉有向图，D的平方图也是超欧拉有向图。因此,假设不存在这种情况。如果n≥2，因为对任意的1≤i＜j≤n，Si和Sj恰有一段公共弧且只存在于Si和 Sj中当且仅当 j=i+1, 所以设 Si：xu1u2…usp0p1p2…pkx和Sj:xv1v2…vtp0p1p2…pkx是n个有向圈中任意两个相邻的恰有一段公共弧的有向圈且x，u1，u2，…，us，v1，v2，…，vt，p0，p1，p2，…，pk∈V（D）。根据 p 次幂有向图的定义容易得到V（D2）=V（D），并且在D的平方图中存在有向路P1：xu1u2…usp0p1p2…pk和有向路 P2：v1v2…vtp0。

下面对k的范围进行分类讨论:

若 k=0，有向路 P1：xu1u2…usp0，有向路 P2：v1v2…vtp0。因为D中有dis（tp0，v1）≤2，dis（tp0，x）≤2，所以有（p0，v1）∈A（D2）和（p0，x）∈A（D2）。因此S（i，）j=P1+（p0，v1）+p2+（p0，x）是 D 的平方图中关于 si和 sj的一个生成有向闭迹。因为si和sj是n个有向圈中的任意两个相邻的恰有一段公共弧的有向圈，且公共弧只存在于si和sj中，所以D的平方图中一定包含一个生成有向闭迹。故D的平方图是超欧拉有向图。

若 k≥1，因为 D 中有 dist(pk，v1)≤2，所以 D 的平方图中存在(pk，v1)。

当k为奇数时,因为在 D中有 dist（p0，p2）=dist（p2，p4）=…=dist（pk-3，pk-1）=dist（pk-1，x）=2,所以D的平方图中存在有向路P3：p0p2p4…pk-3pk-1x。因此S（i，j）=P1+（pk，v1）+P2∪P3是 D 的平方图中关于 si和 sj的一个生成有向闭迹。同理，D的平方图中一定包含一个生成有向闭迹。故D的平方图是超欧拉有向图。

当k为偶数时，因为D中有dist（p0，p2）=dist（p2，p4）=…=dist（pk-2，pk）=2且dist（pk，x）＜2,所以D的平方图中存在有向路 P4:p0p2p4…pk-2pkx。因此，S（i，i+1）=P1+（pk，v1）+P2∪P4是 D 的平方图中关于 si和 sj的一个生成有向闭迹。同理，D的平方图中一定包含一个生成有向闭迹。故D的平方图是超欧拉有向图。

下面介绍的引理1将被应用在证明一个有向图是非超欧拉有向图的例子中。

引理1[10]对于某个正整数m和一个有向图D，如果 V（D）中包含点不交的子集 B1，B2，…，Bm且满足以下两个条件，则称D是非超欧拉有向图:

（1）N-（Bi）Bi∈[m]；

设Fs，t（s，t≥1且满足n=s+t）是一个n个点的强连通有向图,它是通过将一条有向路x1x2…xs加上含有t个新点的集合Y（t），并且连接xs到每一个新点,连接 Y（t）中的每一个点到 x1。令s，t为一个有向图 D的集族，此集族是通过将有向图Fs，t加上形如（xl，xk），1≤k＜l≤s的弧得到的。

若 t=1，即 y1=yt。因为 D∈s，t，所以无论 S 取何值都有S:x1x2…xsy1x1是D中的生成有向闭迹，则D是超欧拉有向图。

若t≥2,下面讨论s的取值范围:

当 s=1,即 x1=xs。因为 D∈s，t，所以 D 中存在（x1，y1）（,y1，x1），（x1，y2），（y2，x1），…，（x1，y）t，（yt，x1）。因此，S=（x1，y1）+（y1，x1）+（x1，y2）+（y2，x1）+…+（x1，y）t+（yt，x1）是D中的生成有向闭迹，则D是超欧拉有向图。

下面讨论s的奇偶性:

y1y2yt圈。因此中的生成有向闭迹，则是超欧拉有向图。

例1说明了定理4中的条件是最优的。

［1］J.Bang-Jensen and G.Gutin.Digraphs:Theory［M］.Algorithms and Applications，Second Edition，Springer，2010.

［2］F.T.Boesch，C.Suffel，and R.Tindell.The spanning subgraphs of eulerian graphs［J］.Journal of Graph Theory，1977，（1）：79-84.

［3］W.R.Pulleyblank.A note on graphs spanned by Eulerian graphs［J］.Journal of Graph Theory，1979，（3）：309-310.

［4］P.A.Catlin.Supereuleriangraphs:asurvey［J］.JournalofGraph Theory，1992，（16）：177-196.

［5］Z.H.Chen,H.J.Lai.Reduction techniques for super-Eulerian graphsandrelatedtopics-asurvey［A］.Combinatoricsand graphtheory'95，Volume1（Hefei），WorldScienceCitation Index Publishing，River Edge，NJ（1995）：53-69.

［6］H.J.Lai，Y.Shao，and H.Yan.An update on supereulerian Graphs［J］.World Scientific and Engineering Academy and Society Transactions on Mathematics，2013，12（9）：926-940.

［7］G.Gutin.Cycles and paths in directed graphs［D］.Tel A－viv-Yafo：Tel Aviv University，1993.

［8］G.Gutin.Connected（g；f）-factors and supereulerian digraphs［J］.Ars Combinatoria，2000，（54）:311-317.

［9］M.J.Algefari，K.A.Alsatami，H.J.Lai and J.Liu.Supereulerian digraphs with given local structures［J］.Information Processing Letters，2016，116（5）：321-326.

［10］K.A.Alsatami,X.D.Zhang，J.Liu and H.J.Lai.On a class of supereulerian digraphs［J］.Applied Mathematics，2016，（7）：320-326.

On Supereulerian Powers of Digraphs

CUI Qiu-yue，LIU Juan*
(Xinjiang Normal University，Urumqi 830017，China)

Adigraph D is supereulerian if contains a spanning closed ditrail.In this paper,we will give the sufficient conditions on a strong digraph or a strong digraph family isobtained for the pthpower of them to be supereulerian：let a digraph has a set of dicycle Γ=｛ S1，S1，…，Sn｝and V（D）=Usi∈ΓV(Si)，the sufficient conditions on its square digraph is supereulerian.For every D∈s，t，ifsis odd，then for everyis supereulerian.Ifsis even，then for everyDDis supereulerian.

supereulerian digraph；pthpower；square digraph；eulerian digraph

O157.5

A

1674-3229（2017）03-0015-05

2017-03-12

国家自然科学基金(61363020,11301450);新疆师范大学研究生科技创新基金资助项目(XSY201602010)

崔秋月(1992-)，女，新疆师范大学数学科学学院硕士研究生，研究方向：图论及其应用。

刘娟(1981-)，女，博士，新疆师范大学数学科学学院教授，研究方向：图论及其应用。