不等定时截尾试验指数分布情形下的可靠性评定

贾　祥, 王小林, 郭　波

(1.国防科技大学信息系统与管理学院, 湖南 长沙 410073;2. 78020部队, 云南 昆明 655000)



不等定时截尾试验指数分布情形下的可靠性评定

贾祥1, 王小林2, 郭波1

(1.国防科技大学信息系统与管理学院, 湖南 长沙 410073;2. 78020部队, 云南 昆明 655000)

摘要：针对产品的可靠性评估问题,一般需要统计分析寿命试验中收集到的试验数据。假如所有试验样品都在不同时刻终止试验,这种方式就是不等定时截尾寿命试验。针对不等定时截尾数据,现有方法大多只能得到参数的点估计,缺乏针对参数置信区间的估计方法。针对这一问题,在指数分布下,根据样本空间排序法这一理论,推导得到一个比现有方法更简单的计算方法。作为对比,基于极大似然估计的性质和bootstrap方法,又提出两个置信下限的近似求解方法。然后,通过蒙特卡罗仿真实验和一个算例,比较了这3个方法。实验表明基于样本空间排序法的计算结果更优。

关键词：样本空间排序法; 指数分布; 不等定时截尾; 置信限

0引言

可靠性是指产品在规定的条件下,在规定的时间内完成规定的任务的能力[1]。可靠性的概率度量称为可靠度。有时,也用寿命这一指标来表示产品的可靠性。针对产品的可靠性评估,往往是对一批产品进行可靠性寿命试验,收集产品的试验时间并进行统计分析,继而评定产品的可靠性。定时截尾试验是可靠性寿命试验的一种常见形式。

一般情况下,定时截尾试验是指在同一时刻终止所有试验样品的试验。文献[2]在指数分布下,基于定时截尾试验数据,得到了分布参数的极大似然估计,但文中并没有讨论如何建立分布参数的置信区间。在指数分布下对定时截尾试验数据进行统计分析,尤其在对参数的置信区间进行求解时,更多地则是考虑其近似解[3-4]。在定时截尾试验中,如果针对所有试验样品,在不同的时刻分别终止试验,这种试验方式就称为不等定时截尾试验。基于这种类型的试验数据,也有研究人员进行了相关研究[5-6]。但这些都只讨论了参数点估计的求解方法,并没有涉及到置信区间的估计方法。

样本空间排序法的提出,为参数估计,尤其是参数的置信区间估计,提供了一条新思路[7-8]。针对不同类型的试验数据和寿命分布,如何根据样本空间排序法建立参数的置信区间,已有相对丰富的研究成果[9-10]。尤其值得一提的是,当前产品的可靠性越来越高,经过寿命试验收集到的试验数据很可能是无失效数据[11]。如果将样本空间排序法运用到无失效问题中,也可以得到不同分布下参数的置信区间估计[12-13]。这是样本空间排序法在实际应用中的一大优势。而针对不等定时截尾试验数据,也已有研究人员根据样本空间排序法,在指数分布下进行了探讨[14-15]。目前相关理论分析已经比较完备[14],但已有的计算方法却非常复杂[15],并且还没有研究来展示其效果。

由此可知,针对不等定时截尾试验数据,对实际中更为关心的参数的置信区间估计,目前仍然缺乏简单有效的的处理方法。这正是本文要解决的问题。指数分布常常被用来描述产品的寿命,因此本文将在指数分布情形下,提出更为简单有效的方法,对不等定时截尾试验数据进行统计分析,并评估产品的可靠性,尤其是对置信下限进行估计。

1模型及参数点估计

首先建立不等定时截尾试验数据的统计模型。假定有n个样品参与寿命试验,依次在截尾时刻点τ1,…,τn(τ1≤…≤τn)处停止试验。若样品i在截尾时刻点τi前失效,则收集到的试验数据就是失效时间,反之就是截尾时间τi。

指数分布的概率密度函数为

(1)

式中,参数θ是平均寿命。若产品寿命X服从参数为θ的指数分布,则记作X～exp(θ)。

引入变量

(2)

式中，Xi为样品i的寿命。当δi=1时,寿命试验收集到的数据为失效时间;反之,试验收集到的是截尾时间。可统一用yi=Xiδi+τi(1-δi)来表示样品i的试验时间。另外,为了后续推导证明的方便,引入符号δ=(δ1,δ2,…,δn)。

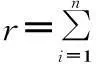
(3)

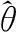
(4)

在指数分布下,可靠度函数是参数平均寿命的单调函数,可靠度的置信下限就是参数平均寿命置信下限的函数。因而估计可靠度的置信下限与估计平均寿命的置信下限是等价的。这样就可以将估计可靠度置信下限转化为估计参数平均寿命的置信下限。首先,基于样本空间排序法的思想,提出一个更为简单有效的估计平均寿命置信下限的方法。其次,作为对比,基于似然估计的性质和bootstrap方法,分别提出两个平均寿命的近似置信下限。最后,通过蒙特卡罗仿真实验和一个算例来比较这些方法的效果。

2基于样本空间排序法的置信下限

2.1样本空间排序法

样本空间排序法是一类通过在样本空间中引入序的概念从而求解参数置信限的理论方法。文献[8]指出,针对取值于非空集合E的随机元Z,若对任何x,y,z∈Z有下列性质:①或者x≥y或者y≥x;②x≥x;③若x≥y,y≥z,则x≥z,那么可在E引入一个二元关系≥,使得E关于≥是一个拟全序集。若进一步引入统计量φ(Z),则相当于在样本空间E中定义了一个序≥如下:当且仅当φ(z1)≥φ(z2)时规定z1≥z2。设μ∈R,对参数空间Θ中的参数θ,令

(5)

(6)

则有

(7)

据此可确定g(θ)的置信下限,具体证明过程可参考文献[8]。为了应用样本空间排序法求其置信下限,常常取g(θ)的某个估计量(如极大似然估计)作为统计量φ。针对不同的具体问题,可选择不同的φ。而应用样本空间排序法的难点也是如何选择φ继而确定G(μ,θ)。

2.2置信下限的求解

(8)

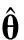
当r=0时,可知此时收集到的试验数据为无失效数据,即所有试验数据全部为截尾时间,此时Xi≥τi(i=1,2,…,n),可得

(9)

当r≠0时,此时

(10)

(11)

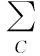
引入变量符号pi=exp(-τi/θ),则可以分别求得P(Xi<τi)=1-pi,P(Xi≥τi)=pi,i=1,2,…,n。则P(r,δ)为

(12)

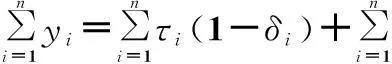
(13)

进一步则有

(14)

式中,υ(u;r,1/θ)为

(15)

根据

(16)

综合式(9)～式(16),可确定式(8)。该结果显然比已有方法[15]要简单。

(17)

(18)

3基于bootstrap方法的置信下限

在本节中,当r>0时,通过bootstrap方法,可以建立平均寿命参数θ的近似置信下限。具体步骤如下:

基于样本量n,原始不等定时截尾试验数据y1,y2,…,yn,n个截尾时刻点τ1,τ2,…,τn及bootstrap自助样本量B:

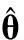
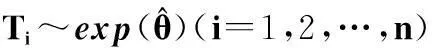
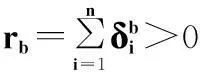
步骤 4基于bootstrap样本和rb,用式(4)可计算得到一个θ的bootstrap估计值,记为θ*。

(19)

4近似置信限法

在本节中,当r>0时,通过极大似然估计的渐进正态性,提出一个参数θ的近似置信下限。

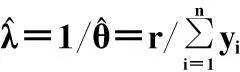
(20)

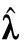
(21)

式中，μα为标准正态分布的α下侧分位数。

Sundberg也基于极大似然估计的渐进正态性,针对定时截尾试验数据,提出了参数θ的近似置信下限[3]。这一结果与式(21)相类似。

5仿真实验

在本节中,通过设计一个蒙特卡罗仿真实验,来对上述方法的优劣进行比较。参看相关文献的实验方法[16],现将本文仿真实验的设计细节说明如下:

(1) 不失一般性,设定指数分布的平均寿命参数为θ=10;

(2) 样本量n设为8、10、12、15、20、30和50,其中n取为8、10、12及15时指代小子样情形,n取为20、30和50则指代大样本情形;

(3) 针对截尾时刻点τ1≤…≤τn的设计,为简化试验过程,令相邻截尾时刻之差相等,即Δ=τi-τi-1(i=2,3,…,n),其中τ0随机生成。在仿真实验过程中,依次取Δ为2、3和4,以观察截尾时刻点的设置对结果的影响;

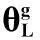
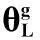
评价置信区间时最常用的2个指标是覆盖率和置信区间平均长度。本文用置信下限平均值来替代置信区间平均长度。如果一个用来求解置信区间的方法是有效的,首先要保证根据该方法得到的覆盖率不小于置信水平,最好是与覆盖率基本吻合,这样可说明该结果既不激进也不保守。在覆盖率与相应的置信水平吻合的基础上,如果置信区间的平均长度更小,或者置信下限平均值更大,则可认为该方法明显优于其他方法。由表1和表2结果可知:

(1) 在表1中,针对覆盖率这一指标,近似置信下限法对应的覆盖率低于相应的置信水平,说明在小子样下,近似置信下限结果偏激进;而bootstrap法的覆盖率则高于相应的置信水平,说明bootstrap近似置信下限偏保守;相比之下,样本空间排序法的覆盖率与相应的置信水平更为吻合,说明在覆盖率这一指标上,样本空间排序法更好。

(2) 针对置信下限平均值这一指标,在表1中,相比之下,基于样本空间排序法得到的置信下限平均值高于bootstrap近似置信下限,低于近似置信下限,说明基于样本空间排序法得到的置信下限结果更合理,而这与上述覆盖率的结果也相吻合。

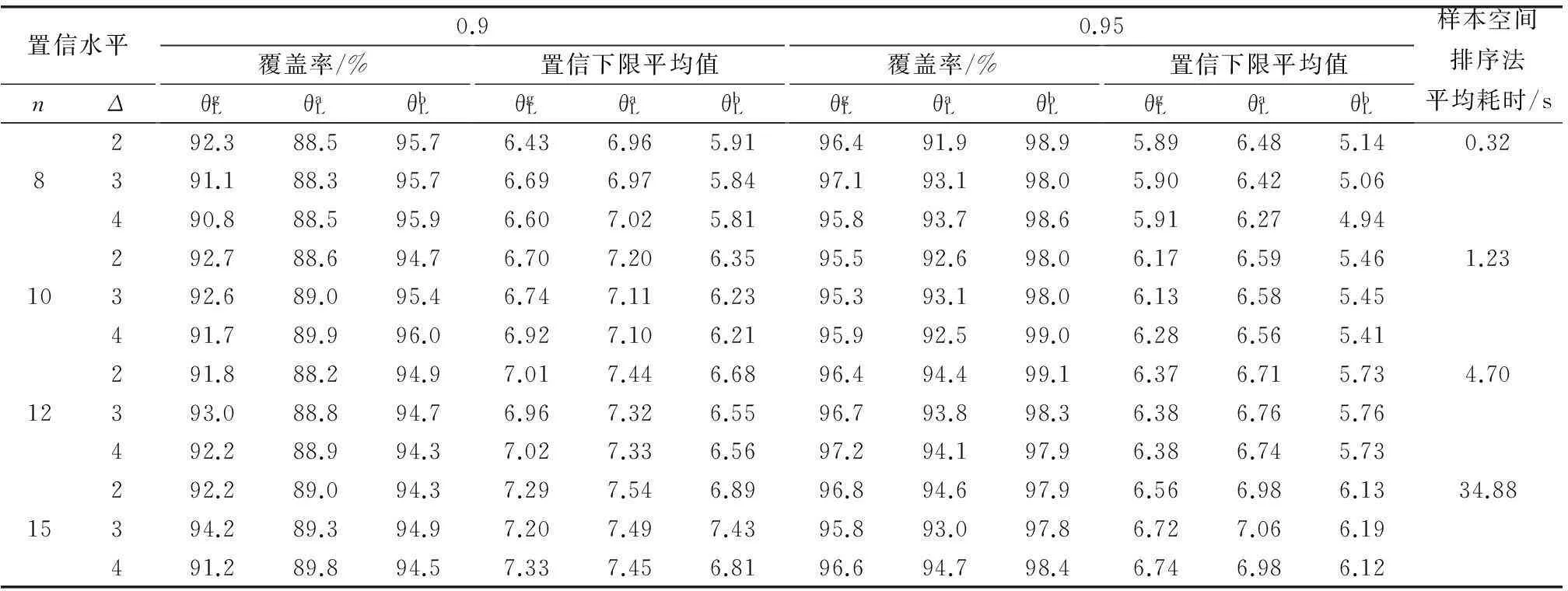
表1　小子样情形下的仿真实验结果

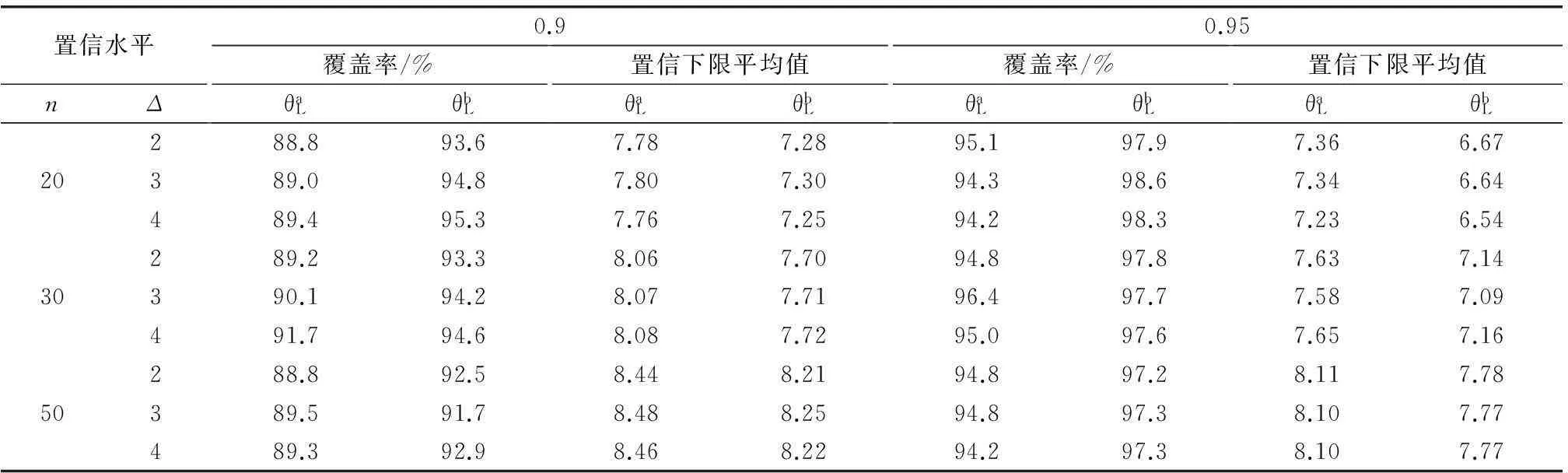
表2　大样本情形下的仿真实验结果

(3) 需要指明的是,由于样本空间排序法引入了序的概念,从而涉及到了变量的组合问题,这使得该方法的计算耗时将随着样本量的增加而增加。这一结论可以从表1中的平均耗时结果得到验证。因此在大样本情形下,即表2中,我们只展示了近似置信下限和bootstrap近似置信下限的计算结果。

(4) 从表2可知,在大样本情形下,近似置信下限和bootstrap近似置信下限的平均值与小子样下相比都有所增大,且近似置信限法的覆盖率变大,bootstrap方法的覆盖率变小,二者都更接近相应的置信水平。这说明,随着样本量的增大,近似置信限法和bootstrap方法的效果都有所提升。而相比之下,近似置信限法的结果更好,因为近似置信限法的覆盖率更接近于相应的置信水平,置信下限平均值更大。

(5) 从表1和表2综合可知,随着n和Δ的增大,3个方法的结果都变得更好,因为这3个方法的覆盖率与相应的置信水平更为吻合,置信下限平均值也随之增加。这也说明,在评估产品可靠性时,样本量越大,截尾时刻点越长,则基于不等定时截尾寿命数据计算得到的可靠性结果越好。

由以上分析可以看出,基于样本空间排序法计算的覆盖率结果更合理,得到的置信下限平均值也更准确。由此,基于覆盖率和置信区间平均长度这两大指标,可证明本文基于样本空间排序法提出的新方法要优于近似置信限法和bootstrap方法。且该方法比已有方法要简单,故本文提出的方法是有效且实用的。另外,在大样本情形下,若要求耗时较短,则可用近似置信下限来替代。

6算例

表3　根据算例数据算得的置信下限

由表中结果可知,针对算例数据,由本文新提出的方法计算得到的置信下限位于近似置信下限和bootstrap近似置信下限之间,这与仿真结果是吻合的。由此再一次证明了本文新提出的方法的准确性和有效性。

7结论

针对不等定时截尾试验收集到的样本数据,本文基于样本空间排序法,提出了一个更简单的计算可靠度置信下限的方法。经过仿真实验分析,可知本文新提出的方法要优于由极大似然估计性质推得的近似置信下限和基于bootstrap方法得到的近似置信下限。另外,若收集到的都是无失效数据,该方法依旧适用。这表明本文新提出的方法是广泛适用的,且有效的。

参考文献：

[1] Guo B, Wu X Y.Analysisofsystemreliability[M]. Changsha: National university of defence technology Press,2002:5-6.(郭波,武小悦. 系统可靠性分析[M]. 长沙: 国防科技大学出版社, 2002: 5-6.)

[2] Bartholomew D J. The sampling distribution of an estimate arising in life testing[J].Technometrics, 1963, 5(3): 361-374.

[3] Sundberg R. Comparison of confidence procedures for type I censored exponential lifetimes[J].Lifetimedataanalysis, 2001, 7(4): 393-413.

[4] Mao S S, Tang Y C, Wang L L.Reliabilitystatistics[M]. Beijing:Senior education Press,2008:106-109.(茆诗松,汤银才,王玲玲.可靠性统计[M].北京:高等教育出版社,2008:106-109.)

[5] Wu Y G. Parameter estimation of commonly used survival distribution based on randomly censored data[D]. Chengdu: Sichuan University, 2005.(吴耀国. 随机删失数据下常用生产分布的参数估计[D]. 成都: 四川大学, 2005.)

[6] Huang C J. Parameter estimation of a class of distribution based on case I interval censored data[D]. Wuhan: Central China Normal University, 2012.(黄传劲. I型区间删失数据下一类分布的参数估计[D]. 武汉: 华中师范大学, 2012.)

[7] Chen J D. The order relations in the sample spaces and the confidence limits for parameters[J].AdvancesinMathematics, 1993, 22(6): 542-552.(陈家鼎. 样本空间中的序与参数的置信限[J].数学进展, 1993, 22(6): 542-552.)

[8] Chen J D.Survivalanalysisandreliability[M]. Beijing: Peking University Press, 2005: 220-230.(陈家鼎. 生存分析与可靠性[M]. 北京: 北京大学出版社, 2005: 220-230.)

[9] Chen J D, Fang X Z. The reliability evacuation in the case of success or failure and the case of exponential distribution[J].JournalofAppliedStatisticsandManagement,2012,31(4):659-669.(陈家鼎,房祥忠.第二讲:成败型情形和指数分布情形的可靠性评定[J].数理统计与管理,2012,31(4):659-669.)

[10] Chen J D, Fang X Z. The reliability evacuation in the case of Weibull or log-normal exponential distribution[J].JournalofAppliedStatisticsandManagement, 2012, 31(5): 835-848.(陈家鼎,房祥忠. 第三讲:Weibull分布和对数正态分布情形的可靠性评定[J].数理统计与管理, 2012, 31(5): 835-848.)

[11] Cai Z Y, Chen Y X, Xiang H C, et al. Method for evaluation of weight expected-Bayesian reliability based on zero-failure data[J].SystemsEngineeringandElectronics, 2015, 37(1): 219-223.(蔡忠义,陈云翔,项华春等.基于无失效数据的加权E-Bayes可靠性评估方法[J].系统工程与电子技术,2015,37(1):219-223.)

[12] Chen J D, Sun W D, Li B X. On the confidence limits in the case of no failure data[J].ActaMathe-maticaeApplicataeSinica, 1995, 18(1): 90-100.(陈家鼎, 孙万龙, 李补喜. 关于无失效数据情形下的置信限[J].应用数学学报,1995,18(1):90-100.)

[13] Han M. Confidence limits of reliability parameters for Weibull distribution[J].JournalofMechanicalStrength,2009,31(1):59-62.(韩明. Weibull分布可靠性参数的置信限[J].机械强度, 2009, 31(1): 59-62.)

[14] Jing G Z, Fang X Z. On the confidence limits for the mean of exponential distribution with non-equal censored time[J].JournalofAppliedStatisticsandManagement, 2000, 19(2): 46-49.(荆广珠,房祥忠. 非等定时截尾寿命试验方案指数分布情形平均寿命的置信限[J].数理统计与管理,2000,19(2):46-49.)

[15] Yan G S, Hou Z Y. The confidence limits of mean life under variant time truncation experiment:a case in exponent distribution[J].JournalofZhengzhouTextileInstitute, 1998, 9(3): 61-65.(严广松,侯紫燕. 不相同定时截尾试验中平均寿命的置信限[J].郑州纺织工学院学报, 1998, 9(3): 61-65.)

[16] Balakrishnan N, Han D, Iliopoulos G. Exact inference for progressively Type-I censored exponential failure data[J].Metrika, 2011, 73: 335-358.

贾祥(1992-),男,博士研究生,主要研究方向为系统可靠性分析。

E-mail: jiaxiang09@sina.cn

王小林(1985-),男,工程师,博士,主要研究方向为系统可靠性分析。

E-mail: wangxiaolin2013@sina.com

郭波(1962-),男,教授,博士,主要研究方向为装备综合保障管理、项目管理与工程管理。

E-mail: boguo@nudt.edu.cn

Reliability evaluation for exponential distribution under non-equal type-I censoring

JIA Xiang1, WANG Xiao-lin2, GUO Bo1

(1 .CollegeofInformationSystemsandManagement,NationalUniversityofDefenseTechnology,Changsha410073,China; 2.Unit78020ofPLA,Kunming655000,China)

Abstract:The problem of reliability evaluation is usually handled based on the sample from the life testing experiment. If all the units in the life test are terminated at different times, it is called the non-equal type-I censoring. According to the non-equal type-I censoring sample, the existing methods usually estimate the parameter without the confidence interval. To fill this gap, a simpler method is proposed to construct the confidence limit on the basis of the order relations in the sample spaces under the exponential distribution. As comparisons, two approximate methods are also proposed based on the bootstrap method and the property of maximum likelihood estimate. Then, a Monte Carlo simulation and an illustrative example are conducted to compare the results of the three methods, which demonstrate that the new method outperforms the others.

Keywords:order relations in the sample spaces; exponential distribution; non-equal type-I censoring; confidence limit

收稿日期：2015-06-15；修回日期：2015-10-07；网络优先出版日期：2015-12-12。

基金项目：国家自然科学基金(71371182)资助课题

中图分类号：TB 114.3

文献标志码：A

DOI:10.3969/j.issn.1001-506X.2016.06.38

作者简介：

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20151222.1415.002.html