改进四元数无味卡尔曼滤波算法

李开龙, 胡柏青, 常路宾

(海军工程大学导航工程系, 湖北 武汉 430033)



改进四元数无味卡尔曼滤波算法

李开龙, 胡柏青, 常路宾

(海军工程大学导航工程系, 湖北 武汉 430033)

摘要：针对四元数无味卡尔曼滤波计算量较大等问题,提出一种改进的四元数无味卡尔曼滤波算法,通过四元数与修正罗德里格斯参数的线性变换,避免了四元数无味卡尔曼滤波中,四元数与误差罗德里格斯参数频繁切换所带来的计算量增大的问题,从而降低了算法的计算量。推导了修正罗德里格斯参数出现奇异值时,改进四元数无味卡尔曼滤波的奇异值避免的转换公式。在捷联惯性导航系统/全球卫星定位系统(strapdown inertial navigation system / global positioning system,SINS/GPS)直接式位置松组合仿真试验中,对比了乘性扩展卡尔曼滤波、四元数无味卡尔曼滤波和改进四元数无味卡尔曼滤波的估计性能,证明了所提出算法的有效性。

关键词：四元数; 姿态估计; 滤波; 组合导航

0引言

姿态估计技术在航空航天、导航等领域中拥有广泛的应用[1-4]。姿态表示方法是研究姿态估计问题的基础,其中有四参量的四元数表示方法和三参量的旋转矢量、罗德里格斯参数族以及Euler角等表示方法[5]。其中罗德里格斯参数族表示方法包含罗德里格斯参数(Rodrigues parameter, RP)、修正罗德里格斯参数(modified Rodrigues parameter,MRP)等姿态表示方法。不同的表示方法具有其特殊性。但是,其中尤为突出的一个特点就是任何三参量的姿态表示方法都无法全局非奇异,而四参量的四元数表示方法却具有全局非奇异的优势[6-7],基于四元数的优越性,其逐渐成为姿态表示当中应用最为广泛的表示方法[8-9]。

姿态估计实现的根本途径是现代滤波技术,Kalman滤波是现代滤波技术当中最主要的技术手段,从线性最优的经典Kalman滤波到应用于非线性系统的扩展Kalman滤波(extended Kalman filter,EKF)、无味Kalman滤波(unscented Kalman filter,UKF),Kalman滤波技术的发展极大地促进了姿态估计研究的进步。在非线性Kalman滤波中,基于无味变换(unscented transformation, UT)的UKF具有比模型线性化的EKF更高的滤波精度[10-11],因此,UKF已经成为非线性滤波体系中研究的重点与热点。

然而,如何将四元数同UKF滤波结合起来,却长期遇到一个关键性问题,即四元数在非线性滤波当中的约束性问题。文献[12-13]提出的四元数无味Kalman滤波算法(quaternion unscented Kalman filter,USQUE)成功解决了该问题,并将该算法从航空姿态估计当中引入到组合导航领域中来,受到广泛地关注。文献[14]也提出了一种“分层滤波”的四元数滤波算法,即采用不存在奇异性的四元数进行外层的姿态更新,采用不存在约束性的旋转矢量表示姿态误差进行内层滤波算法递推。另外,文献[15-16]在文献[14]的基础上,采用惯导基本方程作为滤波模型,研究了在低精度微机械系统(micro electro mechanical systems,MEMS)与卫星导航系统(global navigation satellite system,GNSS)紧组合中的应用等问题。虽然,USQUE算法能够得到较好的姿态估计效果,但是,为了避免四元数维数同四元数滤波方差的维数不匹配的问题,需要利用四元数与误差修正罗德里格斯参数(error-MRP)反复的切换,并且这种切换是通过乘性四元数公式进行的,增大了算法的计算量,使得算法在实际问题中的应用受到了限制。虽然,后续学者对此展开了卓有成效的研究[17-18],但是总结来说其算法都是没有考虑四元数维数同四元数滤波方差的维数匹配性问题的,为了达到降低计算量的效果,将四元数姿态表示部分的滤波方差直接设置为4×4,然而,由于四元数是没有物理意义的参量,因此,这种滤波方差设置是带有极强主观性的。

对此,本文提出一种改进的四元数无味卡尔曼滤波算法(modified USQUE, MUSQUE),利用四元数与MRP线性变换的特点,避免了USQUE算法中乘性四元数变换增大计算量的问题。滤波算法同样采用“分层滤波”的思想,兼顾考虑到四元数维数与四元数滤波方差维数匹配性的问题,在外层采用四元数进行姿态更新,在内层采用MRP进行姿态的递推,同时推导MRP出现奇异值的避免方法。将改进算法应用到捷联惯性导航系统(strapdown inertial navigation system,SINS)/全球卫星定位系统(global positioning system，GPS)直接式组合导航问题中,与乘性扩展卡尔曼滤波(multiplicative extended Kalman filter， MEKF)和USQUE算法进行比较,证明了改进算法在保持较高精度情况下,具有更好的时效性和可信性。

1MRP与USQUE算法

1.1MRP

MRP是一种姿态表示的方法,同四元数和旋转矢量有式(1a)、式(1b)的变

(1a)

(1b)

另外,作为一种三参量的姿态表示方法,MRP是存在姿态奇异点的,通过式(1a)中MRP与旋转矢量的关系可知,MRP将在-2π与2π以及其整数周期点处出现奇异,因此,在采用罗德里格斯参数族姿态表示进行滤波时,需要考虑姿态表示的切换问题以避免奇异,对于MRP来说切换判断点为‖σ‖>1。

1.2USQUE算法

USQUE算法本质上解决了四元数在非线性滤波当中应用的两个问题,其一是解决了四元数在非线性滤波当中约束性的问题;其二是采用 “分层滤波”框架,解决了四元数同滤波方差维数匹配性问题。USQUE算法外层采用四元数进行姿态更新,内层采用error-MRP进行姿态递推方式进行,总结其算法流程如下：

首先定义一个离散的非线性模型

(2)

式中,xk∈Rn为k时刻的状态量；yk∈Rm为k时刻的观测量；f(·)和h(·)分别为系统的状态方程与观测方程；uk-1和vk分别为零均值的系统状态白噪声和零均值的系统观测白噪声,即qk-1～N(0,Qk-1),vk～N(0,Rk)。

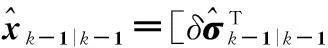
(3)

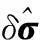
时间更新产生Sigma点

外层姿态更新

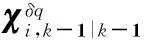
(4)

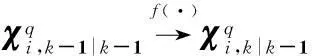
内层姿态递推

(5)

(6)

(7)

量测更新

如果观测方程是非线性的,那么步骤同时间更新类似,如果观测方程是线性的,那么可以利用线性Kalman量测更新过程进行,这里不再赘述。

姿态更新

(8)

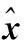
通过以上USQUE算法流程可知,在每步中USQUE算法都将利用乘性四元数关系进行多次error-MRP与四元数的反复切换,这使得算法的计算量增大。据此,提出一种改进的四元数无味卡尔曼滤波算法,在保证精度的前提下,降低其计算量。

2改进四元数无味卡尔曼滤波算法

MUSQUE算法利用四元数与MRP线性变换特点及“分层滤波”思想进行的,其算法流程如下：

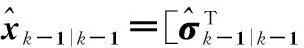
时间更新

产生Sigma点:

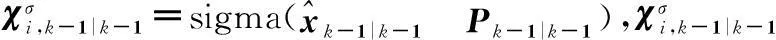
(9)

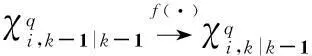
(10)

计算出一步预测状态与滤波方差如式(6)和式(7)所示。

量测更新同时间更新类似,这里不再赘述。

对于‖σ‖>1情况下,采用将四元数与MRP切换转换为四元数与error-MRP切换的方法,即:

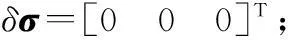
滤波方差切换用Pσ表示基于MRP的滤波方差,用Pδσ表示基于error-MRP的滤波方差。

采用UT变换的形式来保证转换精度,δσ与σ变换采用乘性MRP公

(11)

(12)

(13)

(14)式中

(15)

值得指出得是σ(0)是零时刻的MRP值,这里将零时刻的MRP值作为参考MRP值来进行乘性MRP公式,另外,对于参考MRP的选取,也可以采用类似文献[20]中选取参考四元数的运算形式,虽然文献[20]方法保证了算法的完备性,但是却增大了计算量,因此,这里仍采用零时刻的MRP值作为参考MRP值。

3仿真试验

3.1SINS/GPS直接式组合导航模型

本文采用SINS/GPS直接式位置松组合导航模型进行仿真试验,其中,直接式是指系统状态方程采用捷联惯导基本方程,位置松组合是指观测方程采用GPS提供的位置信息作辅助校正信息。记SINS的载体坐标系 (右-前-上)为b系,地理坐标系或导航坐标系 (东-北-天)为n系,地球坐标系为e系,惯性坐标系为i系。考虑SINS/GPS直接式组合导航方

(16a)

(16b)

(16c)式中

(16d)

(16e)

另外,观测模型考虑SINS/GPS位置松组合模式,则

(17)

式中，vk为零均值的观测白噪声,其方差为Rk。则式(16a)～式(16e)和式(17)构成了SINS/GPS直接式位置松组合导航的系统模型。

3.2对比试验

对比试验中应用SINS/GPS直接式组合导航模型,比较MUSQUE与USQUE和MEKF算法对于姿态、速度与位置估计的精度如图1～图3所示,仿真轨迹如图4所示,记录运动轨迹的姿态trj(qk)、速度trj(vk)和位置trj(pk)信息作为参考,仿真步长Δt为0.1 s,运动轨迹的仿真时间T为1 300 s。

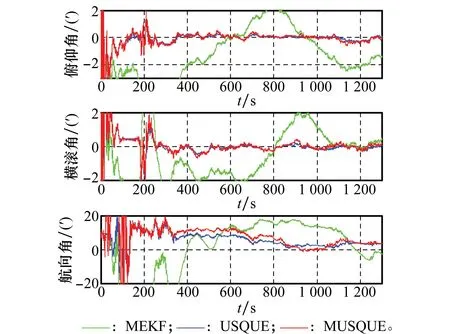
图1　姿态估计结果

特别地,选取如图4所示的仿真轨迹,旋转矢量是大于2π的,MRP将会产生奇异,如果未采取奇异值避免方法,则会产生滤波结果的发散。如图5所示,采用3σ准则来衡量未进行奇异值避免的基于MRP滤波估计结果的可信性,σ是标准差,3σ准则是指理论上滤波估计结果将以99.73%的概率落在±3σ曲线范围内,并且±3σ越接近估计曲线,那么滤波算法越可信。在未进行奇异值避免情况下,基于MRP的滤波估计结果将很快发散,并且3σ准则也证明了滤波结果将不再可信,也就是已经发散。由于MUSQUE是基于四元数与MRP切换的,会遇到奇异性问题。因此,考虑仿真全面性,在该情况下来验证MUSQUE具有较好的估计效果和更小的计算量。

图2　速度估计结果

图3　位置估计结果

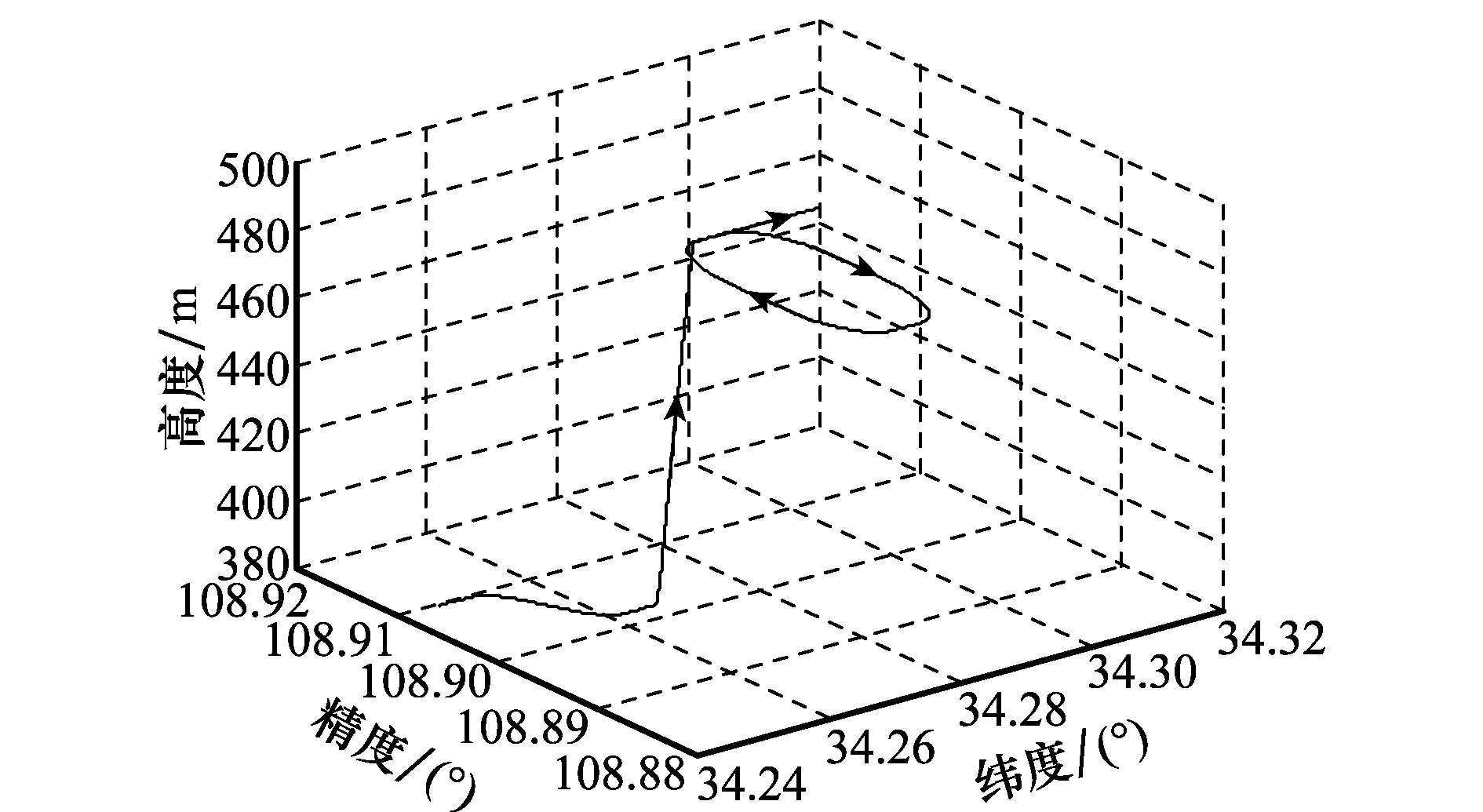
图4　仿真轨迹图

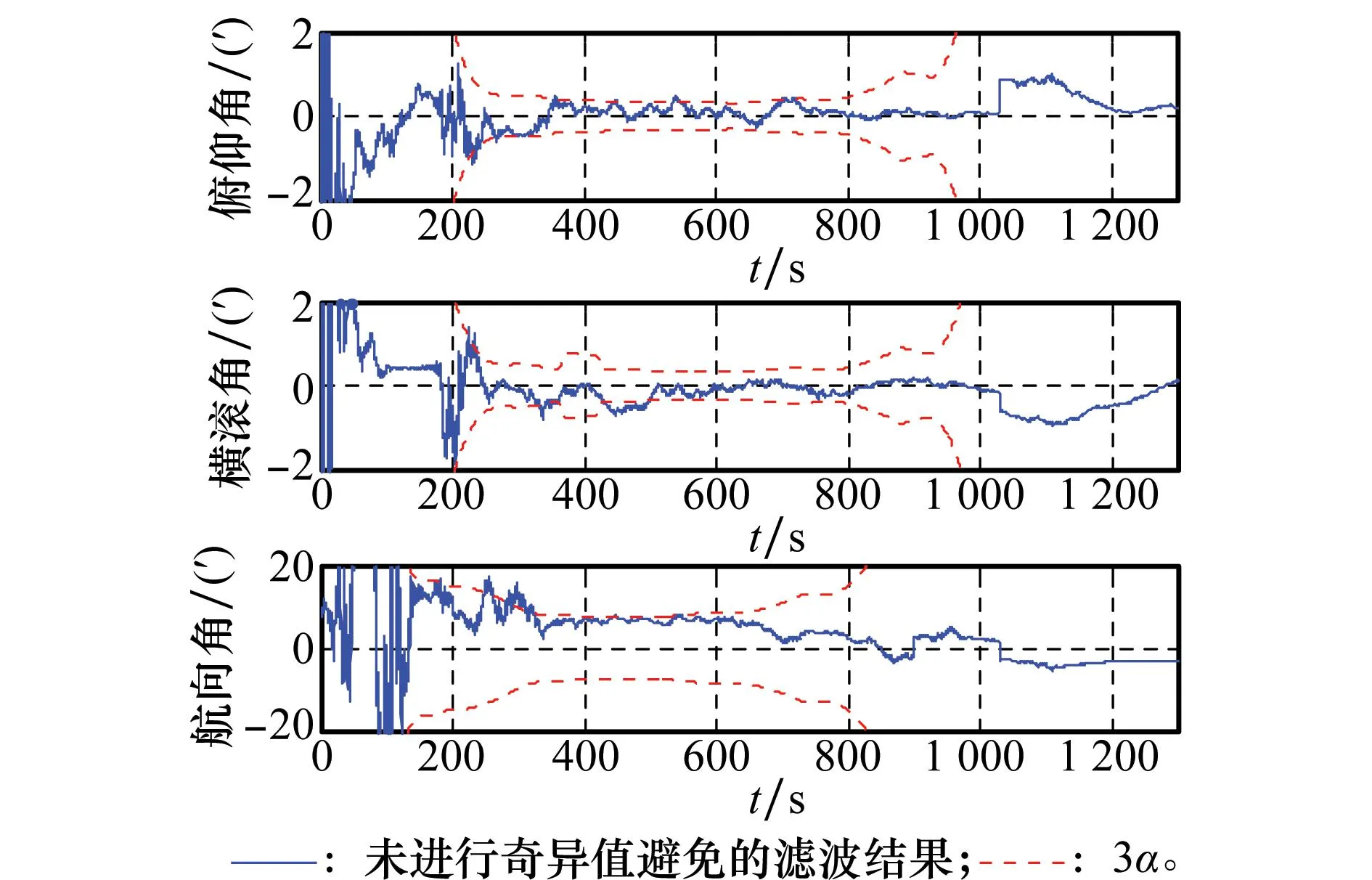
图5　奇异值对MRP的估计影响

设置初始化参数如下所示:

图1～图3是3种滤波的姿态、速度与位置估计误差的结果。从图中可以发现基于UKF滤波框架的USQUE和MUSQUE算法精度均高于基于EKF滤波框架的MEKF。另外,从图中可以发现MUSQUE算法的估计精度同USQUE算法精度是基本相当的,但是算法计算量却降低,这里用算法仿真计算时间来衡量计算量大小,在该次仿真试验中USQUE、MUSQUE与MEKF计算时间分别为172.183 s、136.564 s、105.048 s。MEKF比USQUE和MUSQUE计算时间都要少,这是由于UKF滤波是基于UT变换的,在直接式组合导航中,UT变换产生的每个Sigma点本质上都将进行一次导航解算过程,状态维数越大,产生的Sigma点越多,导航解算的次数也就越多,算法占用的时间也就比模型线性化处理的EKF滤波要大很多。但是,从滤波精度上考虑,USQUE与MUSQUE算法要明显优于MEKF,基于这一点,MUSQUE在精度基本保持不变情况下,降低了算法的计算量,相比USQUE更具有时效性。另外,考虑大失准角度情况下,滤波算法可信性与有效性,设置初始角度为真实角度的30倍,比较USQUE和MUSQUE算法姿态估计精度如图6所示。

图6　大初始误差角情况下算法比较

图6是在大初始误差角情况下USQUE与MUSQUE算法估计效果比较,由图中可知,USQUE与MUSQUE均落在±3σ区域内,但显然,MUSQUE算法的3σ更接近估计曲线,说明MUSQUE比USQUE算法更为可信的。

为了进一步说明算法的有效性,采用蒙特卡罗仿真方法,初始条件不变,蒙特卡罗仿真50次,并分别求取姿态、速度、位置的估计误差均方根值及仿真50次3种算法计算时间的平均值,总结如表1所示(CPUofIntelcorei3-2328M, 2.20GHz,MatlabR2011a)。

表1　平均估计精度及运行时间比较

4结论

USQUE算法为了保持四元数状态维数同四元数滤波方差维数匹配性问题,频繁将四元数与error-MRP进行切换,增大了算法的计算量。针对USQUE算法计算量较大的问题,在兼顾估计精度与匹配性问题的基础上,提出了一种改进的MUSQUE算法,通过四元数与MRP进行线性切换,避免了USQUE算法中通过乘性四元数关系进行切换计算量大的问题,保持了算法的估计精度。同时,推导了在MRP出现奇异时,奇异值避免的解决途径。仿真结果表明,MUQUE相比USQUE在估计精度相当的情况下,具有更低的计算量和更高的可信度,并相比MEKF具有更高的估计精度。

参考文献：

[1] Crassidis J L, Markley F L. Unscented filtering for spacecraft attitude estimation[J].JournalofGuidance,Control,andDynamics, 2003, 26(4): 536-542.

[2] Li J G, Cui H T, Tian Y. Space attitude estimation algorithm abased on multiplicative quaternion and constrained filter[J].SystemsEngineeringandElectronics,2013,35(5):1032-1036.(李建国,崔祜涛,田阳.基于四元数与约束滤波的飞行器姿态估计算法[J].系统工程与电子技术,2013,35(5):1032-1036.)

[3] Suh Y S. Attitude estimation by multiple-mode Kalman filters[J].IEEETrans.onIndustrialElectronics, 2006, 53(4): 1386-1389.

[4] Markley F L, Mortari D. Quaternion attitude estimation using vector observations[J].JournaloftheAstronauticalSciences, 2000, 48(2): 359-380.

[5]Markley F L, Crassidis J L.Fundamentalsofspacecraftattitudedeterminationandcontrol[M]. New York:Springer, 2014.

[6] O’Keefe S A, Schaub H. Shadow set considerations for modified rodrigues parameter attitude filtering[J].JournalofGuidance,Control,andDynamics, 2014: 1-5.

[7] Karlgaard C D, Schaub H. Nonsingular attitude filtering using modified rodrigues parameters[J].JournaloftheAstronauticalSciences, 2009, 57(4): 777-791.

[8] Marins J L, Yun X, Bachmann E R, et al. An extended Kalman filter for quaternion-based orientation estimation using MARG sensors[C]∥Proc.oftheIEEE/RSJInternationalConferenceonIntelligentRobotsandSystems, 2001: 2003-2011.

[9] Markley F L. Fast quaternion attitude estimation from two vector measurements[J].JournalofGuidance,Control,andDynamics, 2002, 25(2): 411-414.

[10] Zhou W D,Qiao X W, Ji Y R, et al. SINS/GPS tightly integrated navigation system based on quaternion square root unscented Kalman filter[J].SystemsEngineeringandElectronics,2010,32(12):2643-2647.(周卫东,乔相伟,吉宇人,等.基于四元数平方根UKF算法的SINS/GPS紧组合导航系统研究[J].系统工程与电子技术,2010,32(12):2643-2647.)

[11] Chang L, Hu B, Chang G, et al. Huber-based novel robust unscented Kalman filter[J].IETScience,Measurement&Technology, 2012, 6(6): 502-509.

[12] Crassidis J L. Sigma-point Kalman filtering for integrated GPS and inertial navigation[J].IEEETrans.onAerospaceandElectronicSystems, 2006, 42(2): 750-756.

[13] Crassidis J L, Markley F L, Cheng Y. Survey of nonlinear attitude estimation methods[J].JournalofGuidance,Control,andDynamics, 2007, 30(1): 12-28.

[14] Shin E H, El-Sheimy N. An unscented Kalman filter for in-motion alignment of low-cost IMUs[C]∥Proc.oftheIEEEPositionLocationandNavigationSymposium, 2004: 273-279.

[15] Yang Y, Zhou J, Loffeld O. Quaternion-based Kalman filtering on INS/GPS[C]∥Proc.ofthe15thIEEEInternationalConferenceonInformationFusion, 2012: 511-518.

[16] Zhou J, Edwan E, Knedlik S, et al. Low-cost INS/GPS with nonlinear filtering methods[C]∥Proc.ofthe13thIEEEConferenceonInformationFusion, 2010: 1-8.

[17] Qian H M, Huang W, Sun L. Cubature Kalman filter with quaternion constraint and its application[J].JournalofHarbinInstituteofTechnology,2014,46(7):41-46.(钱华明,黄蔚,孙龙.四元数约束的容积卡尔曼滤波及其应用[J].哈尔滨工业大学学报,2014,46(7):41-46.)

[18] Zhou W D, Qiao X W, Ren L, et al. Quaternion unsecnted Kalman filter and its application to initial alignment of SINS[J].ChineseJournalofScientificInstrument,2010(2):264-269.(周卫东,乔相伟,任蕾,等.QUKF算法及其在SINS初始对准中的应用[J].仪器仪表学报,2010(2):264-269.)

[19] Soken H E, Hajiyev C. REKF and RUKF for pico satellite attitude estimation in the presence of measurement faults[J].JournalofSystemsEngineeringandElectronics,2014,25(2):288-297.

[20] Chang L, Hu B, Chang G. Modified unscented quaternion estimator based on quaternion averaging[J].JournalofGuidance,Control,andDynamics, 2013, 37(1): 305-309.

[21] Chang L, Hu B, Li A, et al. Strapdown inertial navigation system alignment based on marginalised unscented Kalman filter[J].IETScience,Measurement&Technology, 2013, 7(2): 128-138.

李开龙(1988-),男,博士研究生,主要研究方向惯性导航技术及应用。

E-mail:lee_kailong@163.com,

胡柏青(1964-),男,教授,博士研究生导师,博士,主要研究方向为惯性导航技术及应用。

E-mail:hubaiqing2005@163.com

常路宾(1987-),男,讲师,博士,主要研究方向为惯性导航技术及应用。

E-mail:changlubin@163.com

Modified quaternion unscented Kalman filter

LI Kai-long, HU Bai-qing, CHANG Lu-bin

(DepartmentofNavigationEngineering,NavalUniversityofEngineering,Wuhan430033,China)

Abstract:Aiming at the problem of larger calculation burden of the quaternion unscented Kalman filter (USQUE), a modified USQUE (MUSQUE) is proposed. Based on the transformation between the quaternion and the modified rodriguez parameter (MRP), the novel method can reduce calculation amount by avoiding frequent transformation between the quaternion and the error-MRP for the USQUE. Meanwhile, the singularity avoidance method is also derived in case when the MRP is singularity. By simulating strapdown inertial navigation system/global positioning system (SINS/GPS) direct integrated navigation, the results prove the validation of the novel method comparing with the multiplicative extended Kalman filter and USQUE.

Keywords:quaternion; attitude estimation; filter; integrated navigation

收稿日期：2015-04-04；修回日期：2015-11-17；网络优先出版日期：2016-02-15。

基金项目：国家重点基础研究发展计划(973计划)(2012CB719902)；国家自然科学基金(61304241,61374206,41374082)资助课题

中图分类号：U 666.12

文献标志码：A

DOI:10.3969/j.issn.1001-506X.2016.06.28

作者简介：

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20160215.1436.006.html