指数分布与其它分布的关系
2011-10-20刘国祥
刘国祥
(赤峰学院 数学与统计学院,内蒙古 赤峰 024000)
指数分布与其它分布的关系
刘国祥
(赤峰学院 数学与统计学院,内蒙古 赤峰 024000)
从指数分布的特征出发,通过了讨论讨论指数分布与其它分布的关系,从而体现了指数分布在概率统计中的作用.
概率统计;指数分布;正态分布;均匀分布;几何分布
正态分布、均匀分布、指数分布是最常用的三个连续型分布.由于正态分布和均匀分布具有明显的集合直观,常见并且易于理解的现实模型,因此在教材[1,2]和文献中对于它们的讨论都比较详细.而关于指数分布的讨论相对就比较少[3,4],没有引起人们的足够认识.
下面从指数分布的特征出发,分几个方面通过了讨论讨论指数分布与其它分布的关系,从而体现了指数分布在概率统计中的作用.
1 指数分布及其特征
连续型随机变量X的分布密度函数
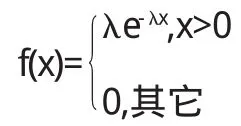
其中λ>0,称随机变量X服从参数为λ的指数分布.
指数分布的分布函数为
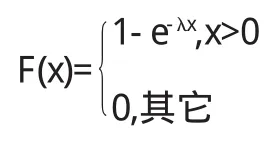
指数分布的数学期望和方差分别是
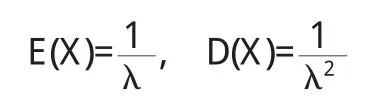
指数分布的最大特征就是无记忆性:
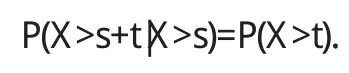
文献[1]指出,指数分布是唯一具有无记忆性的连续型分布.
2 指数分布与几何分布的关系
如果随机变量X服从参数为P的几何分布,则它的概率分布律是:
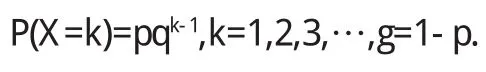
由于对于任意的正自然数 有
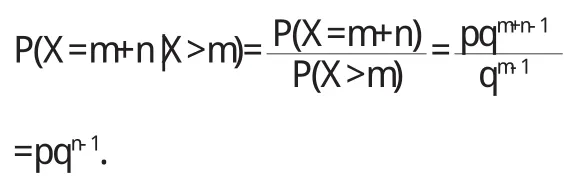
因此几何分布具有无记忆性的离散型分布.并且,几何分布是唯一具有无记忆性的离散型分布[1].
几何分布的数学期望:

它的数学期望与指数分布具有相同的参数的倒数形式.
为什么几何分布与指数分布有如此多的相同形式呢?服从指数分布的随机变量表示的是某些“易碎品”的“寿命”,如电子元件、玻璃制品等.虽然它们的“寿命”与多种因素有关,但是有一种因素是决定性的,也就是“致命”的.它正好与“服从正态分布是与多种相互独立的因素有关,但是没有一种因素是起决定作用”相反.
而几何分布是一种“直到……为止”型的概率分布,也是一种“寿命”.
电子元件的“寿命”服从指数分布,如果电子元件是否损坏的决定因素是电压,在连续使用过程中,虽然有多种因素,但是“直到”电压达到元件不可承受范围内,它的“寿命”就“为止”.
相互独立的射击,直到击中为止,射击次数服从几何分布.被枪手离散地射击,直到击中,它的“寿命”就“为止”了.
从而我们看到,几何分布与指数分布具有相同的原理,只是其一为离散型,另一个为连续型.所以具有许多相同(或相似)的性质.
3 指数分布与泊松分布的关系
泊松分布是重要的离散型分布,他与社会生活密切相关,如电话交换台中来到的呼叫次数、公共汽车站来到的乘客数、放射性分裂落到某区域的质点数,甚至母鸡下蛋的个数、鸡蛋孵化成小鸡的个数.
指数分布与泊松分布有如下的关系:
定理1 设随机变量X服从参数为λt的泊松分布,则时间两次发生之间的“等待时间”Y服从参数为λ的指数分布.
证明 由于随机变量X服从参数为λt的泊松分布,则它的分布律为:
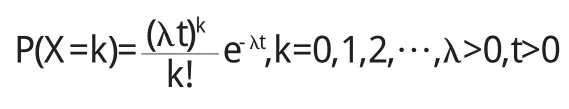
设事件前一次发生的时刻为0.
因为Y不可能为负数,所以当
t≤0时显然有P(Y≤t)=0,
而t>0时,因为在“等待时间”内事件不发生,

则由概率的连续性,Y分布函数

Y服从参数为λ的指数分布.
单位时间内母鸡下蛋的个数服从泊松分布,而两次下蛋的时间间隔服从指数分布.
4 指数分布与均匀分布的关系
指数分布和均匀分布同为连续型分布,它们之间有如下关系:
定理2 随机变量X服从参数为λ的指数分布的充分必要条件是随机变量
Y1-e-λX服从(0,1)上的均匀分布.
证明 由于随机变量X服从参数为λ的指数分布,
则X概率密度函数

则Y概率密度函数
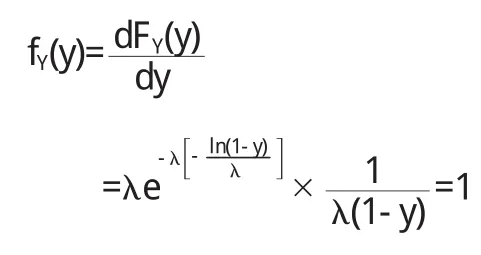
从而Y=1-e-λX服从(0,1)上的均匀分布.
另一方面,如果Y=1-e-λX服从(0,1)上的均匀分布.
则Y概率密度函数
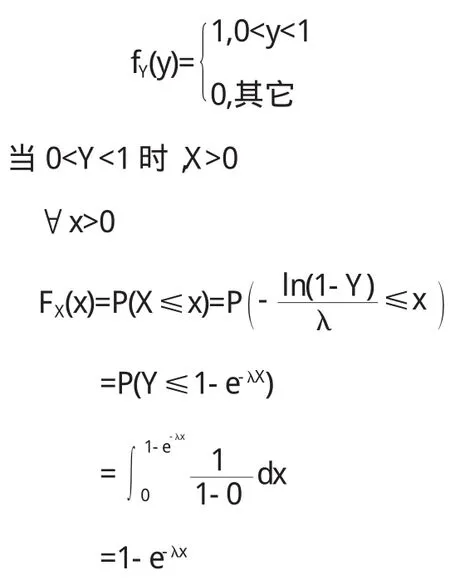
从而,则X概率密度函数
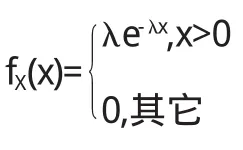
则随机变量X服从参数为λ的指数分布.
5 指数分布与正态分布的关系
指数分布和正态分布同为连续型分布,正态分布可以说是最重要的一种概率分布.它和指数分布之间有如下关系.
定理3随机变量X,Y相互独立,都服从正态分布N(0,λ2),则Z=X2+Y2服从指数分布.
证明 显然Z=X2+Y2≥0,
由于随机变量X,Y相互独立,则(X,Y)的联合分布密度函数为
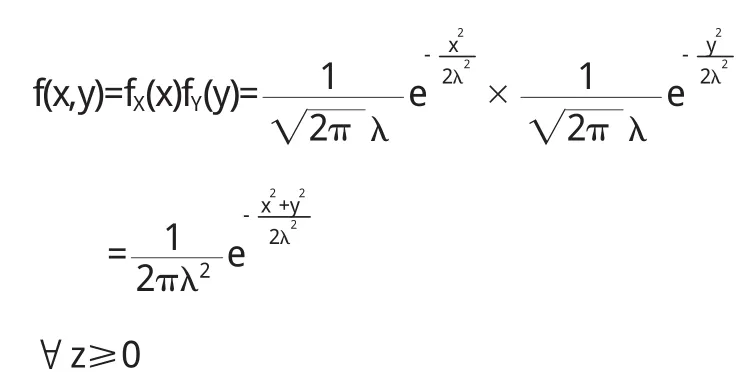
随机变量Z的分布函数
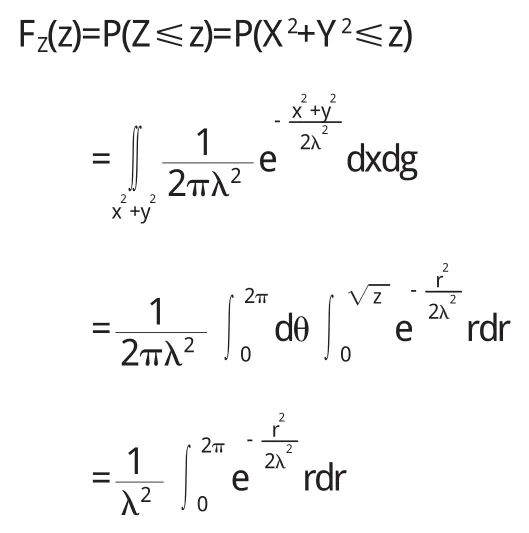
则Z的分布密度函数为
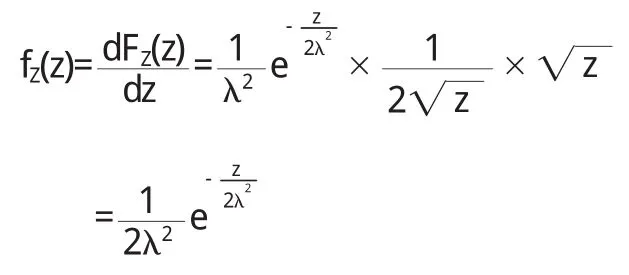
所以,则Z=X2+Y2服从参数为的指数分布.
6 指数分布的推广形式
经典教材[1,2]都只介绍了二元均匀分布和二元正态分布而没有涉及二元指数分布.文献[3]给出了指数分布的一种推广形式,并在文献[4]把它应用到药物在机体内分布中.文献[5]介绍了多元Marshll-Olkin型指数分布.
埃尔兰分布的密度函数为
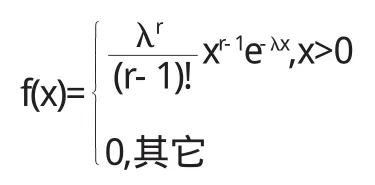
其中r是正整数,λ>0.
当r=1时,就是指数分布.则埃尔兰分布就是指数分布的一种推广形式.
Γ分布的密度函数为
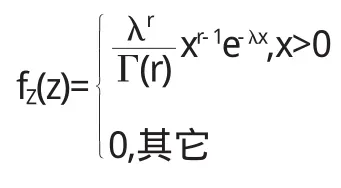
其中r>0,λ>0.
它是埃尔兰分布的推广,当然也是指数分布的一种推广形式.
此外,关于分布的可加性:同泊松分布且相互独立的n个随机变量之和仍服从泊松分布,同正态分布且相互独立的n个随机变量之和仍服从正态分布,同两点分布且相互独立的n个随机变量之和仍服从二项分布,同正态分布且相互独立的n个随机变量的线性组合仍服从正态分布.
Γ分布的的可加性是:如果X1,……Xn相互独立,Xi,i=1,2,3,…,服从参数为αi,λ的Γ分布,则服从参数为αi,λΓ分布.
但是,它的特殊形式指数分布:同指数分布且相互独立的n个随机变量之和服从Γ(n,λ)分布或者χ2(2n)分布.已经不是指数分布.
例如:n=2,α1=α2=1,Z=X1+X2的概率密度为
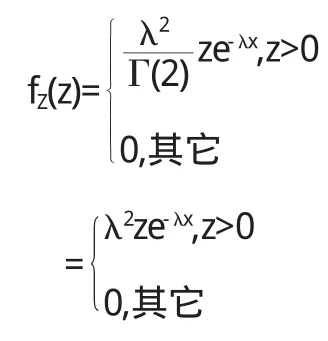
他不是指数分布.当然χ2分布也具有可加性.
〔1〕李贤平.概率论基础(第二版)[M].高等教育出版社,1979.4,116,128.
〔2〕魏宗舒,等.概率论与数理统计教程[M].高等教育出版社,1983.10.
〔3〕刘国祥.广义指数分布[J].赤峰学院学报,2007,(3):1-8.
〔4〕刘国祥.药物在机体内分布的数学模型[J].赤峰学院学报,2008,(3):15-16.
〔5〕李国安.多元Marshll-O lkin型指数分布的特征及其参数估计[J].工程数学学报,2005,22(6):1055-1062.
O221.8
A
1673-260X(2011)12-0012-03
