指数分布与几何分布的条件可加性

何朝兵

（安阳师范学院数学与统计学院，河南安阳 455000）

指数分布与几何分布的条件可加性

何朝兵

（安阳师范学院数学与统计学院，河南安阳 455000）

首先证明了独立指数分布随机变量之和的一个条件分布是指数分布，然后证明了独立几何分布随机变量的一个线性组合的一个条件分布是几何分布.

指数分布;几何分布;相互独立;条件分布;可加性

指数分布不但在电子元器件方面得到了普遍使用，而且可靠性工程和排队论的丰富实践又使人们加深了对指数分布性质的认识.几何分布已经应用于越来越多的领域，特别是在信息工程、电子工程、控制论以及经济学等领域都具有极其重要的地位.指数分布和几何分布有许多相似的性质，可参看文献［1－10］.因此，探讨这2个分布的性质是一个有意义的研究方向，具有重要的理论价值和实用价值，而且会使这2个分布在可靠性数学等应用概率模型中的应用更加广泛.众所周知，2个独立的指数分布随机变量的和不服从指数分布，如果添加特定的条件，独立指数分布随机变量的和服从指数分布吗?对于几何分布也有类似的情况.对于这个问题，却很少有文献报道.但这个问题的解决将会丰富和完善指数分布和几何分布的分布理论.

1 预备知识

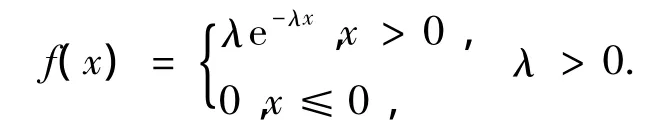
则称X服从参数为λ的指数分布，记为X～exp（λ）.

定义2 如果随机变量X的分布律为

则称X服从参数为p的几何分布，记为X～Geo（p）.

定义1 如果随机变量X的密度函数为

2 主要结论

假设X1，X2，…，Xn是连续型随机变量，因为P（X1=X2=… =Xn）=0，所以无法用条件概率直接计算，那么一个很自然的想法是:

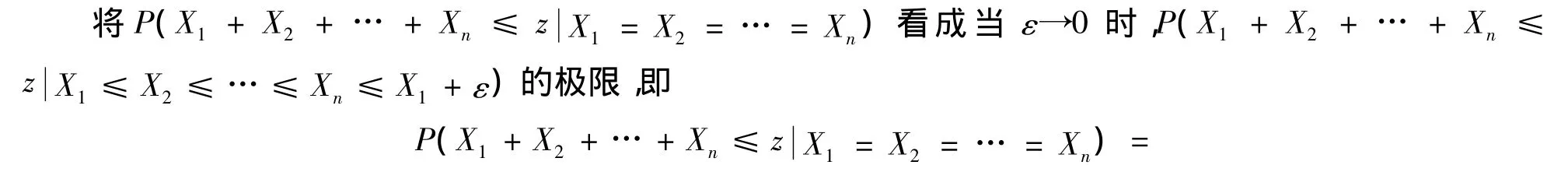
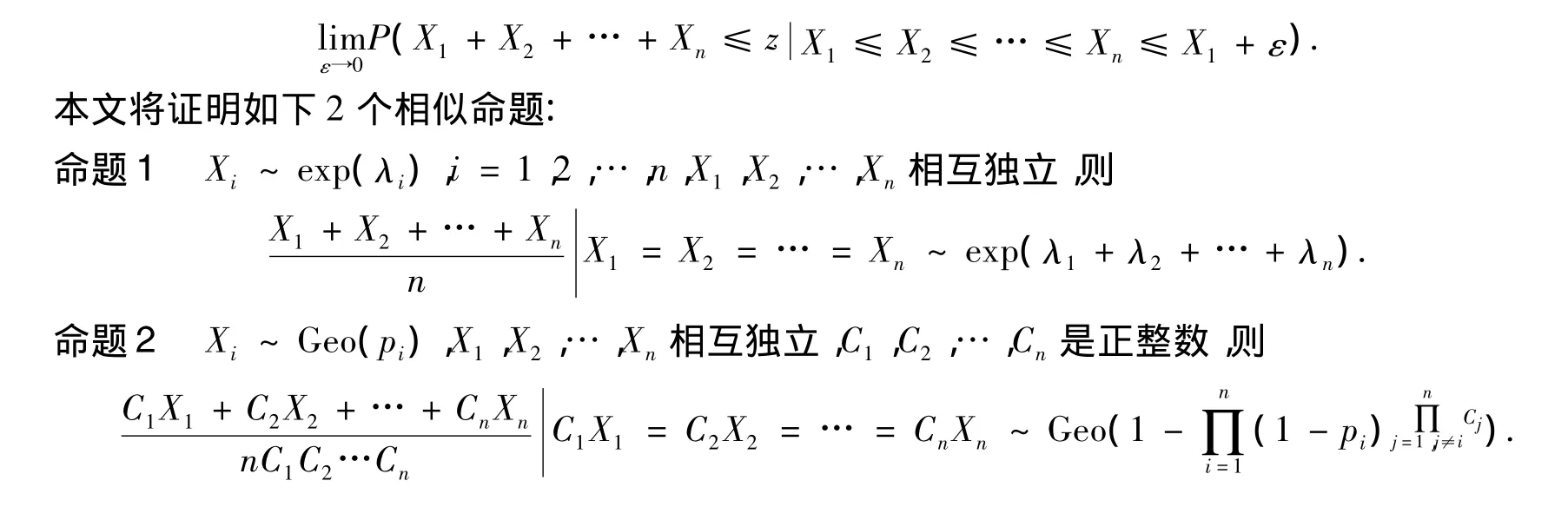
3 结论的证明

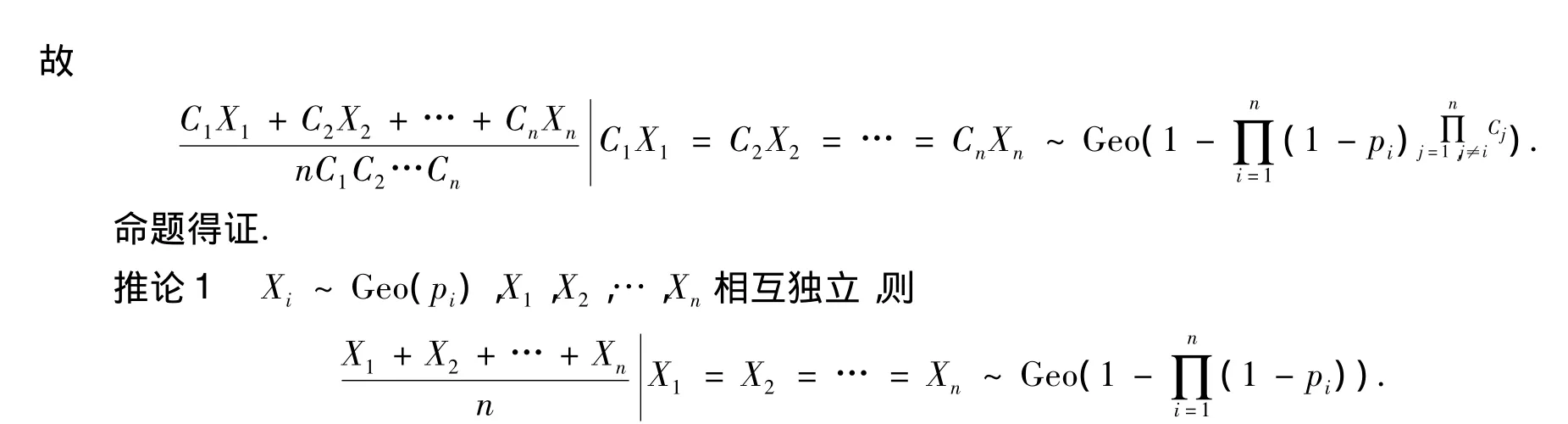
命题2很容易证明推论1.

由推论1可以看出，若X，Y相互独立，且都服从几何分布Geo（p），如果已知X=Y，则其中

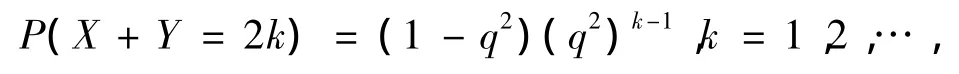
其中q=1－p.

［1］曹晋华，程侃.可靠性数学引论［M］.北京:高等教育出版社，2006:15，25，365－405.

［2］茆诗松，汤银才，王玲玲.可靠性统计［M］.北京:高等教育出版社，2008:97－160.

［3］KA S L.Characterization of the exponential distribution by the relevation transform［J］.Appl.Prob.，1990，27（3）:726－729.

［4］ROSSITZA D.Characterization of geometric and exponential random variables［J］.Communications in Statistics Theory and Methods，2004，33（8）:1755－1765.

［5］BEST D J，RAYNER J C W.Test of fit for the geometric distribution［J］.Communication in Statistics Theory and Methods，2003，32（5）:913－928.

［6］LAWRENCE M L.Probabilistic properties of exponential distribution［J］.Microelectron.Reliab，1988，28（2）:257－262.

［7］毛用才.基于顺序统计量的几何分布特征的进一步结果［J］.纯粹数学与应用数学，1995，11（2）:115－119.

［8］徐晓岭，费鹤良，王蓉华.几何分布的两个统计特征［J］.应用概率统计，2006，22（1）:10－20.

［9］徐晓岭，王蓉华，费鹤良.几何分布的几个性质［J］.数学研究，2008，41（1）:103－112.

［10］吴绍敏，程细玉.几何分布恒加应力寿命试验下的混合数据分析［J］.华侨大学学报:自然科学版，1997，18（1）:6－10.

［11］华东师范大学数学系.数学分析.下册［M］.北京:高等教育出版社，2004:174.

Additivity of Exponential Distribution and Geometric Distribution under Certain Condition

HE Chao-bing

（School of Mathematics and Statistics，Anyang Normal University，Anyang 455000，China）

In the paper，it was proved that a conditional distribution of sum of independent exponential random variables is exponential distribution，and it was also proved that a conditional distribution of a linear combination of independent geometric distribution variables is still geometric distribution.

exponential distribution;geometric distribution;independent;conditional distribution;additivity

O 211.3

A

1004－1729（2012）01－0020－06

2011－09－26

河南省教育厅自然科学基金资助项目（2009B110003）

何朝兵（1975－），男，河南周口人，安阳师范学院数学与统计学院讲师，硕士.