基于MGF研究指数分布与其他分布之间的关系
2018-11-23朱芳汪慧
朱 芳 汪 慧
(安徽新华学院通识教育部 安徽合肥 230088)
一、引言
指数分布是概率论与数理统计[2]中非常重要的一种分布类型,是分析和解决统计学问题中常用的工具之一,在概率论与数理统计研究中具有非常重要的实际应用价值。近些年来,很多学者基于MGF深入研究统计学、代数学以及其他学科,并取得了很多显著的成果[3][4][5].本文主要基于MGF的定义及性质研究指数分布与其他几种分布之间的内在联系,旨在进一步介绍概率论中几种特殊的分布,帮助学生在课堂之余丰富概率知识,并了解概率论的博大精深。首先给出MGF的定义及一些重要的性质。

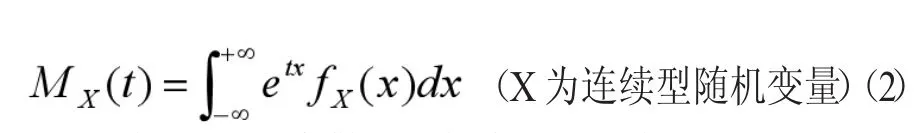
其中Px(x)为离散型随机变量X的概率函数;fx(x)为连续型随机变量x的概率密度函数。
性质1.1 设随机变量X,Y的动差生成函数存在,且Z=X+Y,则有:

性质1.2 设随机变量Y=a+bX(a,b为任意的常数),则有:

由MGF定义和性质得出指数分布、泊松分布、Laplace正态分布和Gamma分布的MGF:

表1 指数分布、泊松分布、Laplace分布和Gamma分布的MGF
二、指数分布其他几种分布之间的关系
(一)指数分布与泊松分布。设随机变量X~E(λ),Y~Poisson(λt),Y 表示某事件在时间段[0,T]内发生的总次数,令Y为该事件第一次发生的时间,则有:
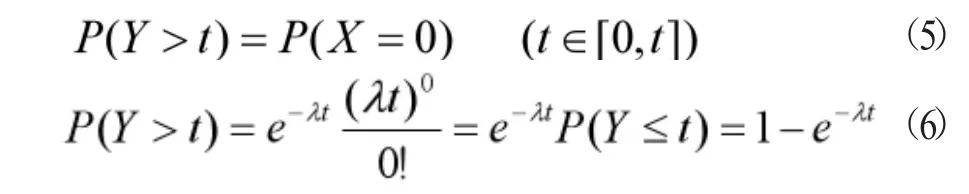
等式两边同时求导得:

因此可以看出随机变量为指数分布。
定理2.1 泊松分布在某种情况下可以近似为指数分布。
(二)指数分布与Laplace分布。设随机变量X1~E(1),X2-E(1),且随机变量 Z=X1-X2,X1,X2,Z,的 MGF 分别记为MX1(t),MX2(t),MXz(t)。
结合表格1知X~E(1)的指数分布的动差生成函数为:

结合MGF的性质得:
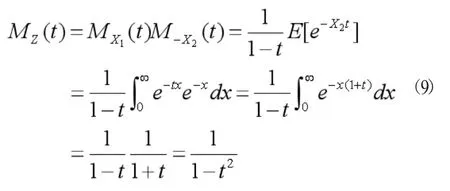
设 Z0~Laplace(0,1),则有:
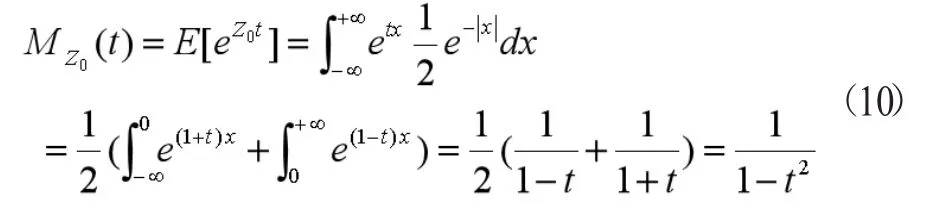
定理 2.2 当 X1~E(1),X2~E(1)时,X1-X2.~Laplace(0,1)。
(三)指数分布与 Gamma分布。设随机变量 X1~E(1),记随机变量,的MGF分别记为,且,
则由MGF的性质得:

假设 W~Gamma(n,λ),则可以计算出:
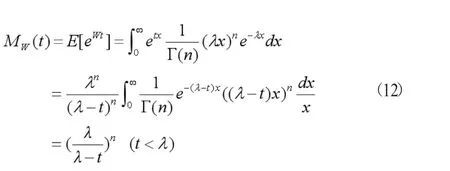
定理2.3 参数相同的多个指数分布的和即为Gamma分布。
三、结语
通过三个定理的简单证明,可以看出指数分布与其他三种分布之间的内在联系,说明在特定情况下分布之间是可以相互转化的.本文主要基于MGF研究指数分布与泊松分布、Laplace正态分布及Gamma分布三者之间的关系,帮助学生在学习课堂知识之余更加深入的理解几类重要分布,感受概率论的博大精深,为后期统计学的学习奠定基础,实现多角度的辅助教学,这样既可以满足学生对知识探索的需求,也可以丰富教学内容.
