二元Weinman型指数分布随机变量之和、差、积、商及比率的分布

李国安

(宁波大学理学院，浙江宁波315211)



二元Weinman型指数分布随机变量之和、差、积、商及比率的分布

李国安

(宁波大学理学院，浙江宁波315211)

[摘要]出于水文科学应用的需要，本文导出了二元Weinman型指数分布随机变量之和、差、及比率的精确分布；计算了二元Weinman型指数分布随机变量之积、及商的精确分布，所得结果可应用于水文科学的教学和研究之中.

[关键词]二元Weinman型指数分布； 和； 积； 比率； 水文科学

1引言

Weinman[1]于1966年引入了如下的二元指数分布

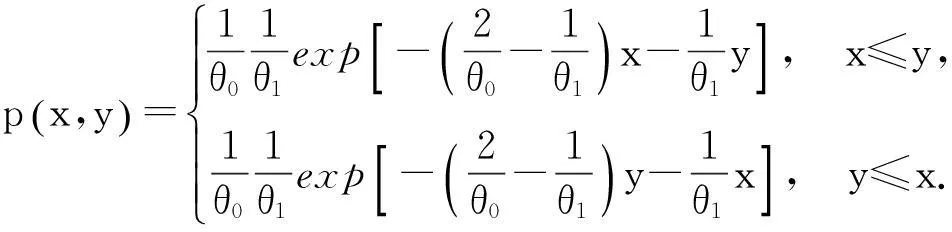
它是所有不独立的二元指数分布中所含参数最小的二元指数分布，同时又是一个对称指数分布，称之为二元Weinman型指数分布，文献[2]获得了来自二元Weinman型指数分布II型截尾样本的应力—强度结构系统可靠度的一致最小方差无偏估计；文献[3]对它的特征及参数估计问题进行了研究，导出了二元Weinman型指数分布的一个特征，获得了参数的最大似然估计及矩估计，给出了二元Weinman型指数分布的二种模拟，还得到了强度为二元Weinman型指数分布时并联结构系统可靠度的估计；几乎与此同时，国外学者对二元指数分布随机变量之和、积、商的分布展开了研究，文献[4]研究了二元Gumbel指数分布随机变量之和、积、比率的分布；文献[5]研究了二元Freund型指数分布随机变量之和、积、比率的分布；文献 [6]研究了二元Lawrance-Lewis型指数分布随机变量之和、积、比率的分布；文献[7]研究了二元downton型指数分布随机变量之和、积、比率的分布；文献[8]研究了可靠性模型中的五类二元指数分布，分别研究了二元downton型、Arnold-Strauss型、Marshall-Olkin型、Freund型、Lawrance-Lewis型指数分布随机变量之和的精确分布.出于教学和科研二方面的需要：本文导出了二元Weinman型指数分布随机变量之和、差、积、商、及比率的精确分布.

2二元Weinman型指数分布随机变量之和、差、及比率的分布

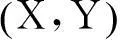
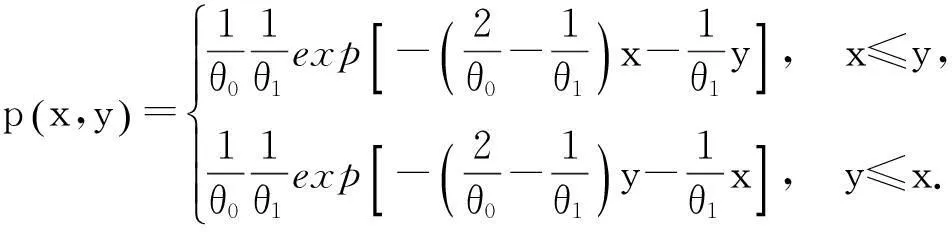
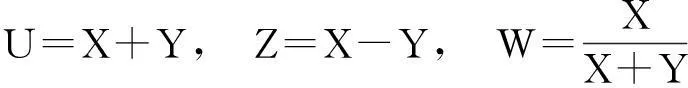
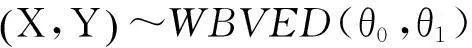
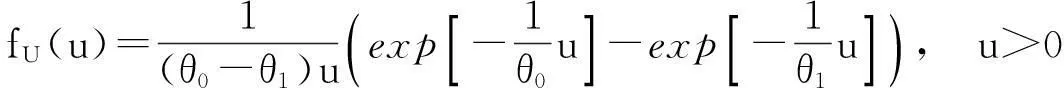
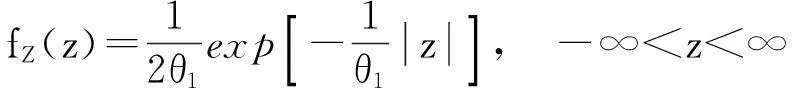
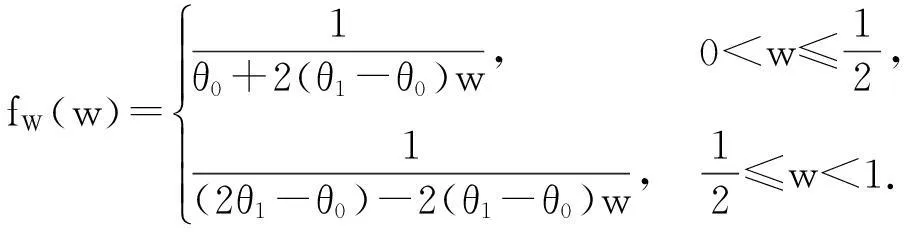
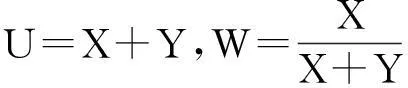
由

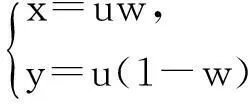
得行列式

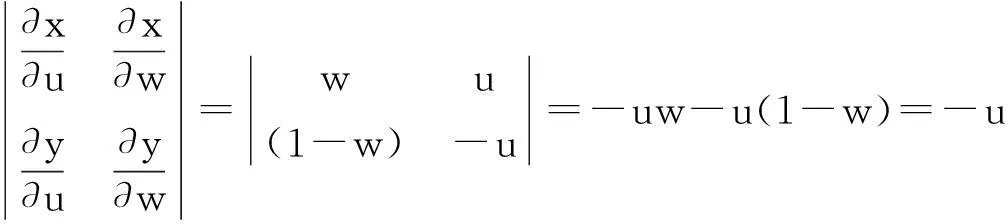
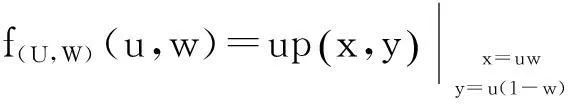
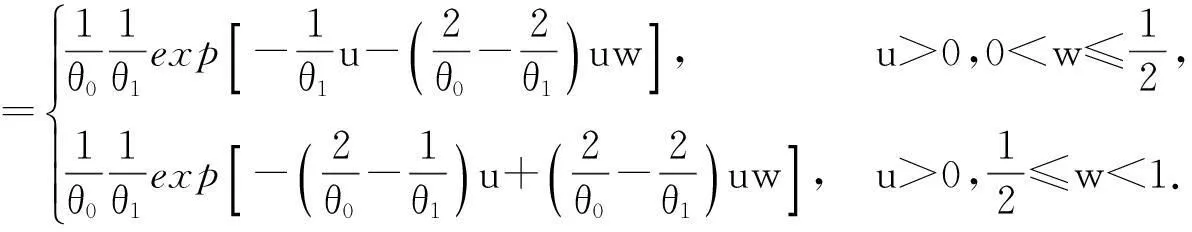
由此得

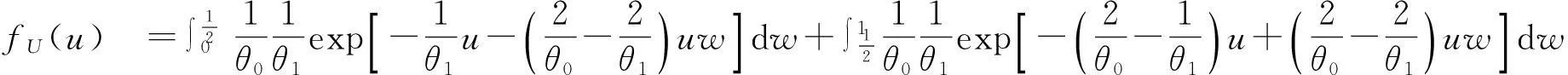
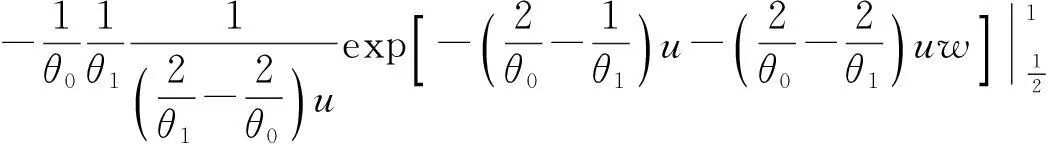
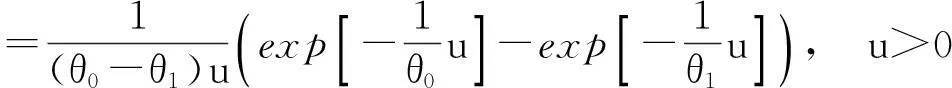
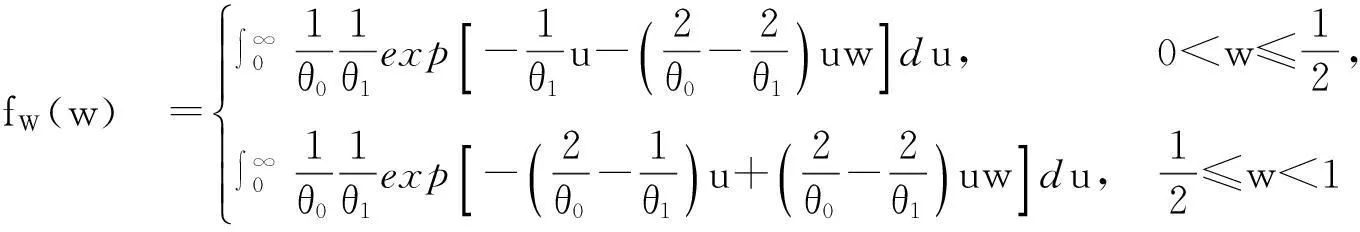
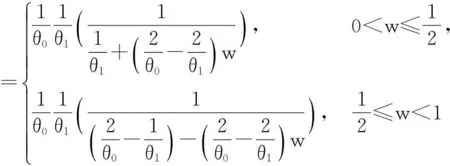
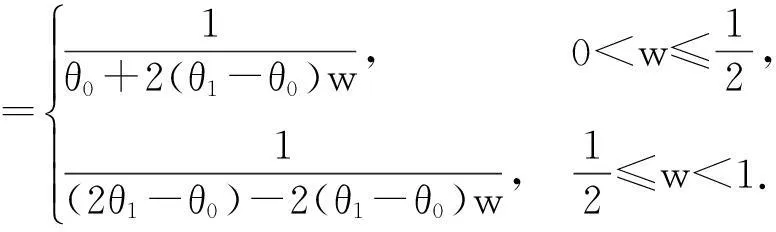
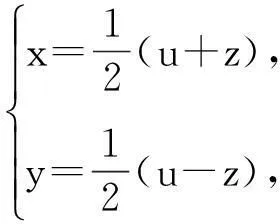
得行列式

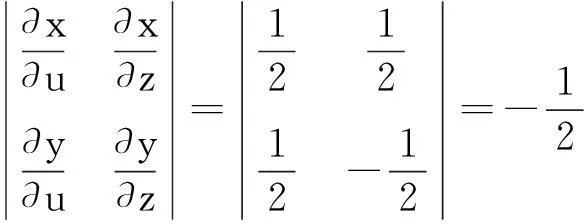
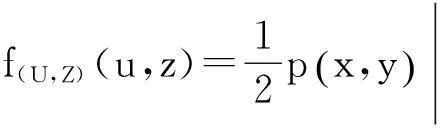
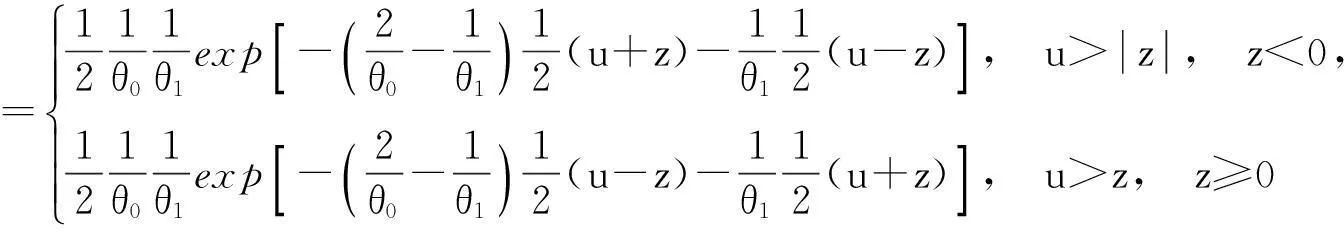
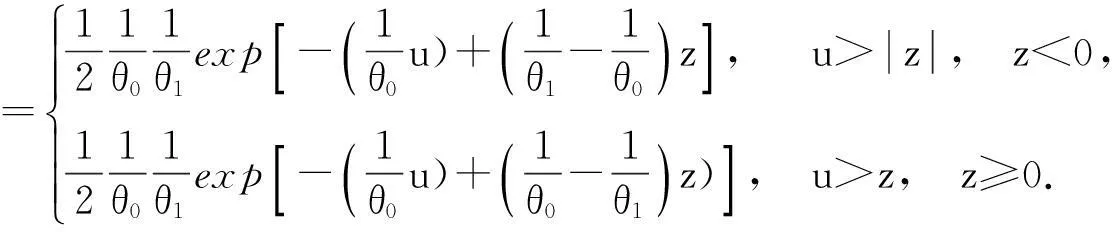
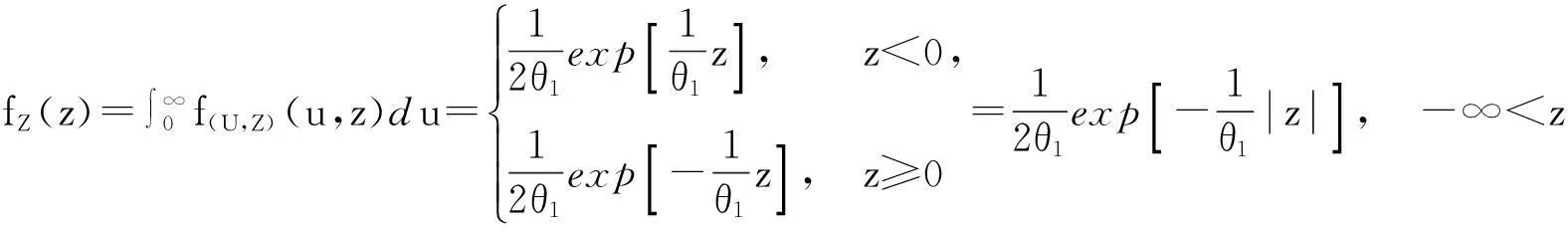
3二元Weinman型指数分布随机变量之积、及商的分布

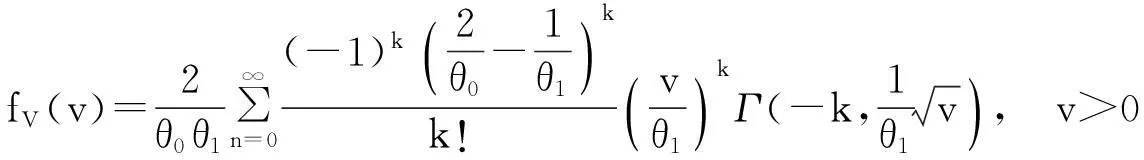
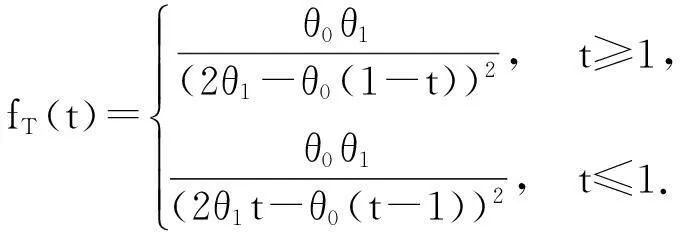
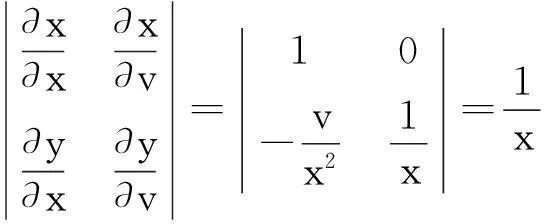
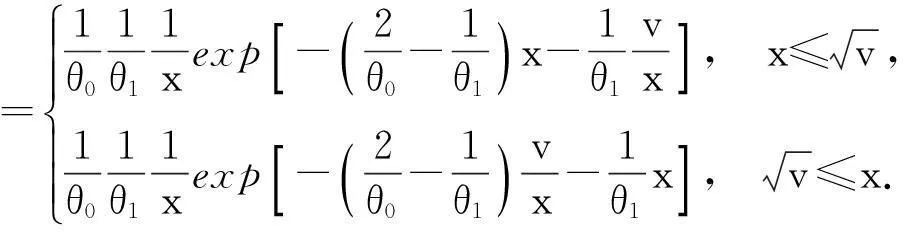
由此得

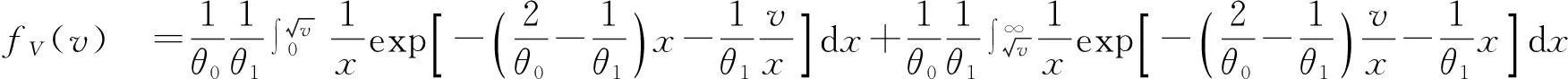
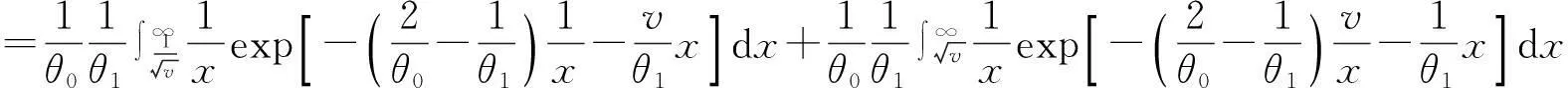
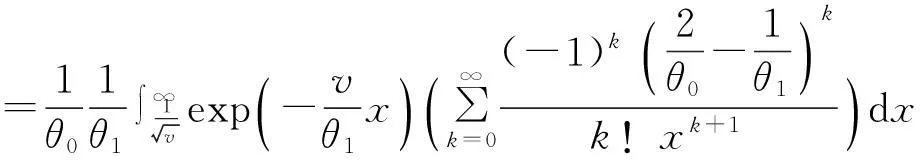
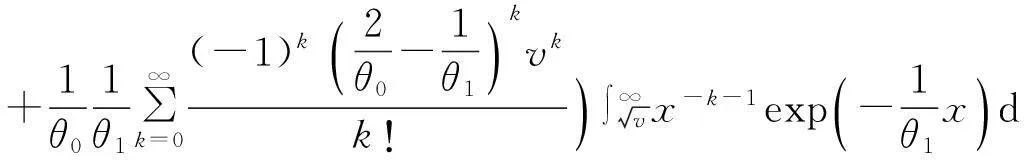
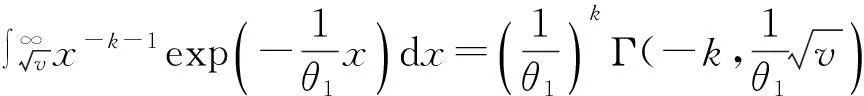
分别代入，合并得

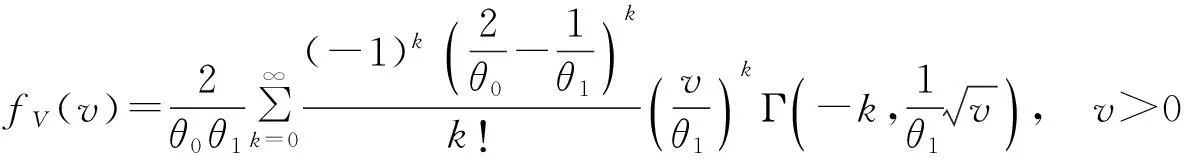
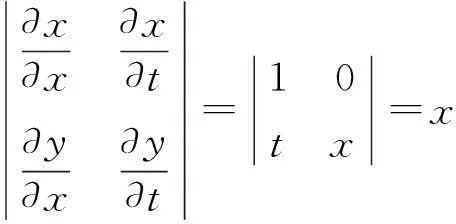
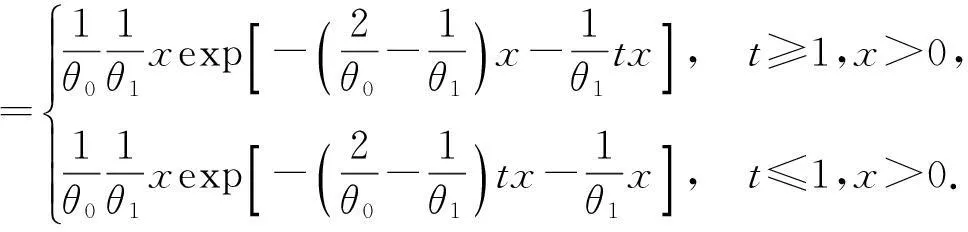
由此得

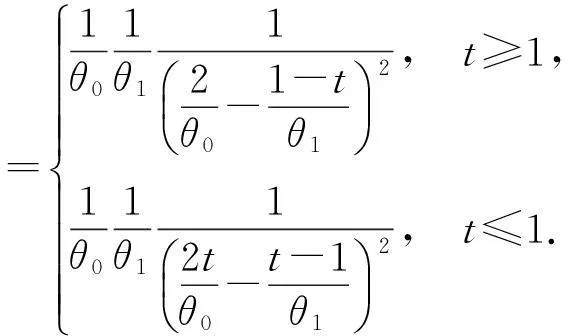
得

[参考文献]

[1]Weinman D G.A multivariate extension of the exponential distribution[D].Ph. D. thesis, Arizona State University, 1966.

[2]Cramer E，Kamps U.The UMVUE of P{X

[3]李国安.二元Weinman型指数分布的特征及其应用[J].数学研究与评论，2005，25(2)：337-340.

[4]Nadarajah S.Sums, products, and ratios for the bivariate gumbel distribution[J].Mathematical and Computer Modelling，2005，42：499-518.

[5]Gupta A K，Nadarajah S.Sums, products, and ratios for Freund’s bivariate exponential distribution[J].Applied Mathematics and Computation，2006，173：1334-1349.

[6]Saralees Nadarajah S，Ali M M.The distribution of sums, products and ratios for Lawrance and Lewis’s bivariate exponential random variables[J].Computational Statistics & Data Analysis，2006，50：3449-3463.

[7]Nadarajah S，Kotz S.Sums, products, and ratios for downton’s bivariate exponential distribution[J].Stoch Environ Res Risk Assess，2006，20：164-170.

[8]Nadarajah S，Kotz S.Reliability models based on bivariate exponential distributions[J].Probabilistic Engineering Mechanics，2006，21：338-351.

[9]Arnold B C，Strauss D J.Bivariate distributions with exponential conditionals[J].Journal of the American Statistical Association，1988，83：522-527.

[10]Marshall A W，Olkin I.A multivariate exponential distribution[J].Journal of the American Statistical Association，1967，62(1)：30-44.

[11]Nadarajah S.Exact distributions of XY for some bivariate exponential distributions[J].Statistics: A Journal of Theoretical and Applied Statistics, 2006，40(4)：307-324.

[12]Block, H W and Basu, A P. A continuous bivariate exponential extension[J].Journal of the American Statistical Association，1974，69：1031-1037.

[13]Nadarajah S，Gupta A K.Friday and Patil’s bivariate exponential distribution with application to drought data[J] ].Water Res. Manag. 2006，20：749-759.

[14]Friday D S，Patil G. P.A bivariate exponential model with applications to reliability and computer generation of random variables [C] . in: C.P. Tsokos, I. Shimi (Eds.), Theory and Applications of Reliability, vol. I, New York ：Academic Press, 1977：527-549.

Sums, Minus, Products, Quotients, and Ratios for Weinman’s

Bivariate Exponential Distribution

LIGuo-an

(Department of Mathematics, Ningbo University, Ningbo, Zhejiang 315211, China)

Abstract:Motivated by hydrological applications，the exact distribution of U=X+Y，Z=X-Y， when X and Y follow Weinman’s bivariate exponential distribution is derived in this paper；also, The exact distribution of V=XY，T=XY when X and Y follow Weinman’s bivariate exponential distribution is calculated， the results can be applied to hydrological sciences.

Key words:Weinman’s bivariate exponential distribution; sums; products; ratios; hydrological sciences

[中图分类号]O212.4

[文献标识码]C

[文章编号]1672-1454(2015)05-0114-06

[基金项目]宁波大学学科项目(XKL14D2037)

[收稿日期]2014-11-02