指数分布抽样基本定理及在指数分布参数统计推断中的应用
2016-12-19李国安
李国安
(宁波大学理学院,浙江宁波315211)
指数分布抽样基本定理及在指数分布参数统计推断中的应用
李国安
(宁波大学理学院,浙江宁波315211)
发现指数分布抽样基本定理,应用到指数分布参数的统计推断中,得到了指数分布参数的一致最小方差无偏估计;并且得到了单总体指数分布参数的置信区间及联合置信区间,以及双总体指数分布参数比值及差的置信区间.
指数分布抽样基本定理; 统计推断; 一致最小方差无偏估计; 置信区间; 联合置信区间
1 引 言
正态分布抽样基本定理在一般的数理统计教材[1,2]中都会提到,但在这二本教材中,并没有出现指数分布抽样基本定理,那么只有二种情况,一种是指数分布抽样基本定理的相关结果已有,参见文献[3]中相关内容,但是没有以指数分布抽样基本定理的形式写出来;另一种,是用到了指数分布抽样基本定理的相关结果,但没有足够重视到这是指数分布抽样基本定理[3],作者认为:首先指数分布抽样基本定理一直未出,其可能的原因在于,通常讲的指数分布,指称单参数指数分布,本文作者在研究二元帕累托分布参数的一致最小方差无偏估计问题中,发现了所谓的指数分布抽样基本定理,它是针对二参数的指数分布;其次,平行于正态分布是概率统计分布中最重要的分布,指数分布是精算生存分布中最重要的分布;最后,若是数理统计教材[1,2]中关于顺序统计量的分布,一直未把指数分布抽样基本定理当作例子,会让读者认为不存在指数分布抽样基本定理,为此,作者特作此文,期望能把指数分布抽样基本定理的相关内容写进教材.
2 指数分布抽样基本定理
指数分布总体的顺序统计量(X(1),…,X(n))的联合分布如下
定义1 设X~E(λ),X1,…,Xn是来自X~E(λ)的容量为n的样本,(X(1),…,X(n))有如下的密度函数
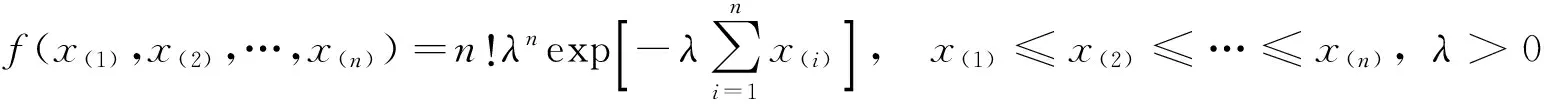
则称(X(1),…,X(n))服从多元顺序统计量型指数分布,记作(X(1),…,X(n))~NVED(λ).

(i)2nλX(1)~χ2(2);
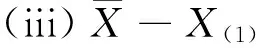
证 由
P(X(1)>x(1))=P(X1>x(1),…,Xn>x(1))=exp[-nλx(1)],
所以g(x(1))=nλe-nλx(1),x(1)>0,即2nλX(1)~χ2(2);
记U(i-1)=X(i)-X(1),i=2,…,n.V=X(1),u(i-1)=x(i)-x(1),v=x(1),得x(i)=u(i-1)+v,i=2,…,n.x(1)=v,则(U(1),…,U(n-1),V)的联合分布密度为
所以(U(1),U(2),…,U(n-1))是来自总体U~E(λ)的容量为n-1的样本(U1,U2,…,Un-1)的顺序统计量,(U1,U2…,Un-1)与X(1)相互独立.所以
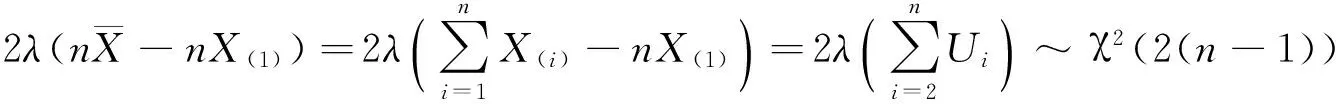
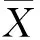
3 指数分布参数的一致最小方差无偏估计
定义2 设X~E(λ,μ),是指X有如下的密度函数
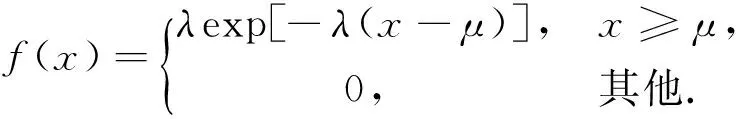
定理2 Xj,j=1,…,n是来自总体X~E(λ,μ)的容量为n的一个样本,则参数λ,μ的最大似然估计分别为
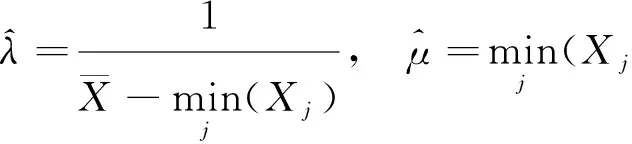
证 由
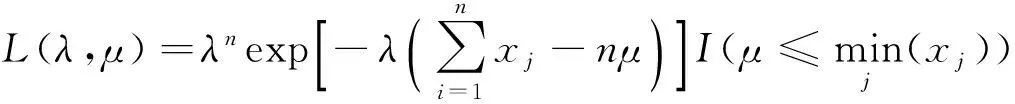
μ的最大似然估计为
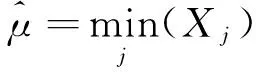
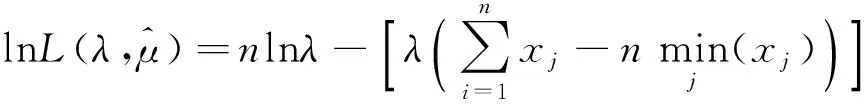
令
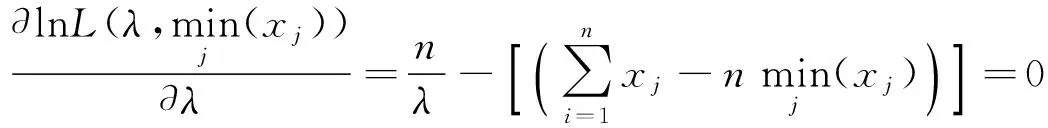
得λ的最大似然估计为
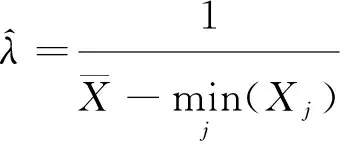
定理3 Xj,j=1,…,n,是来自总体X~E(λ,μ)的容量为n的一个样本,则参数λ,μ的一致最小方差无偏估计分别为

证 由指数分布抽样基本定理得
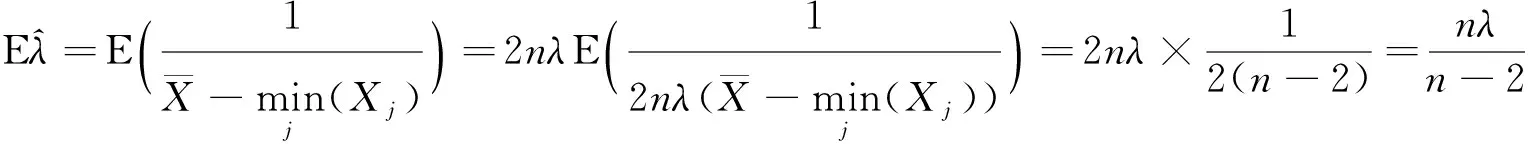
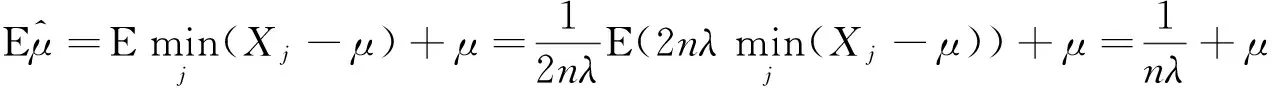
所以
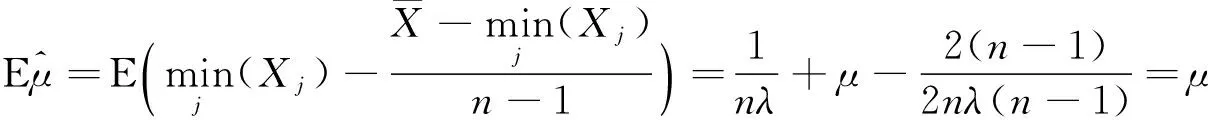
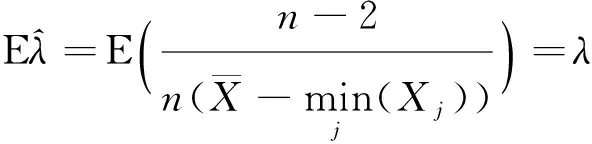
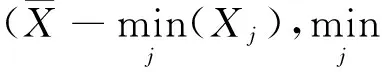
4 指数分布参数的置信区间
定理4 Xj,j=1,…,n是来自总体X~E(λ,μ)的容量为n的一个样本,则参数λ,μ的置信度为(1-α)%的置信区间分别为
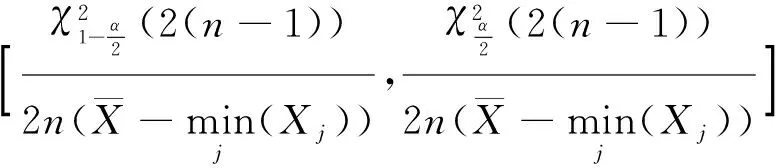
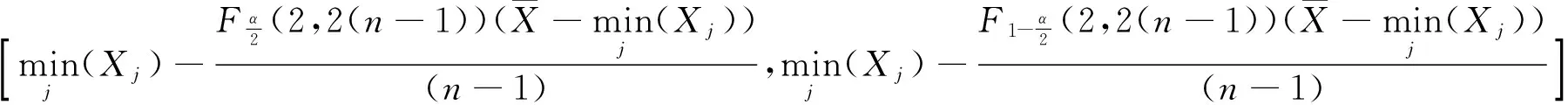
λ,μ的置信度为(1-α)%的联合置信区间为
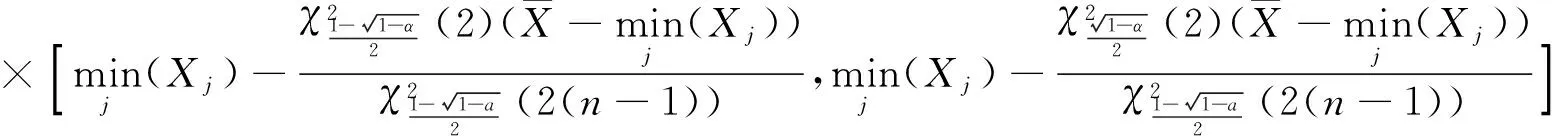
证 由指数分布抽样基本定理

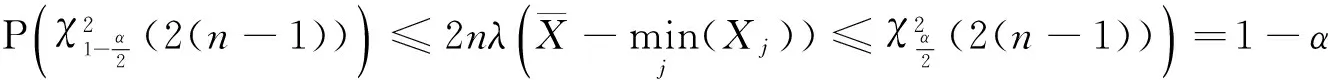
得
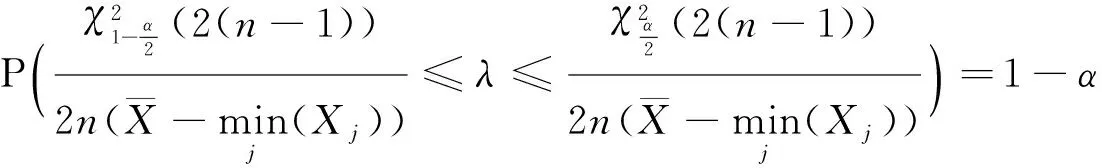
λ的置信度为(1-α)%的置信区间为
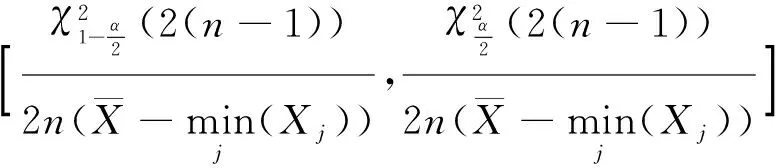
由
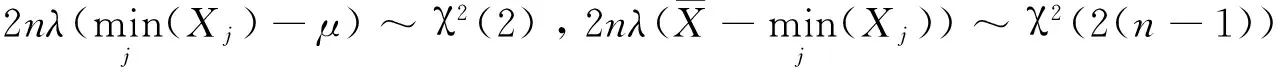
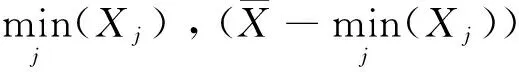
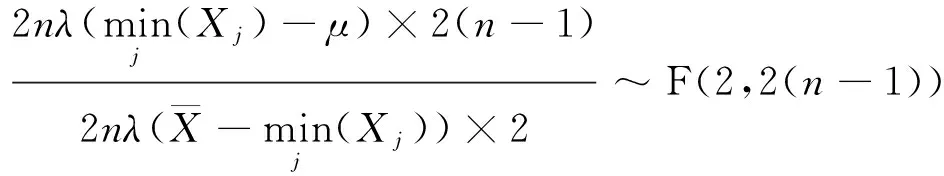
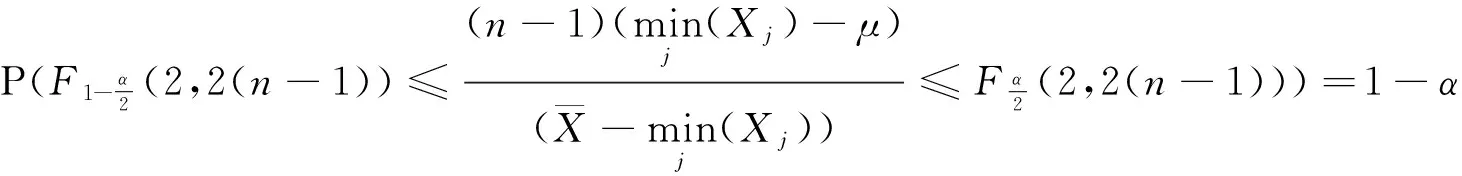
=1-α.
μ的置信度为(1-α)%的置信区间为
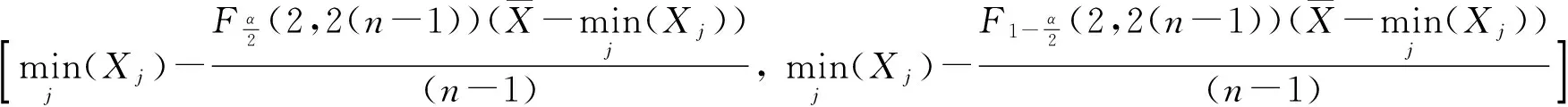
由
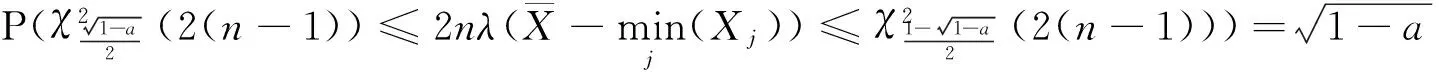
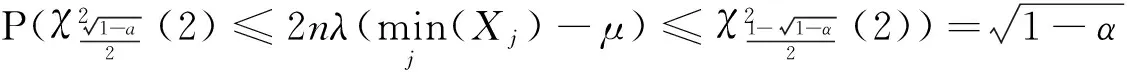
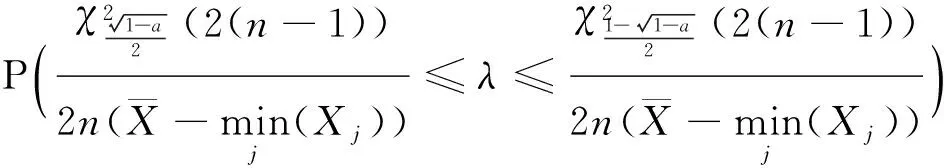
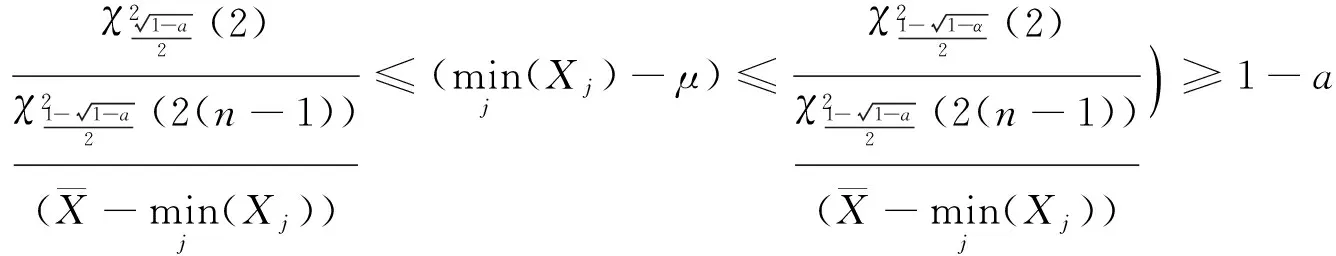
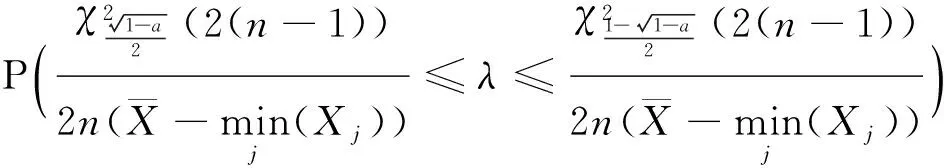
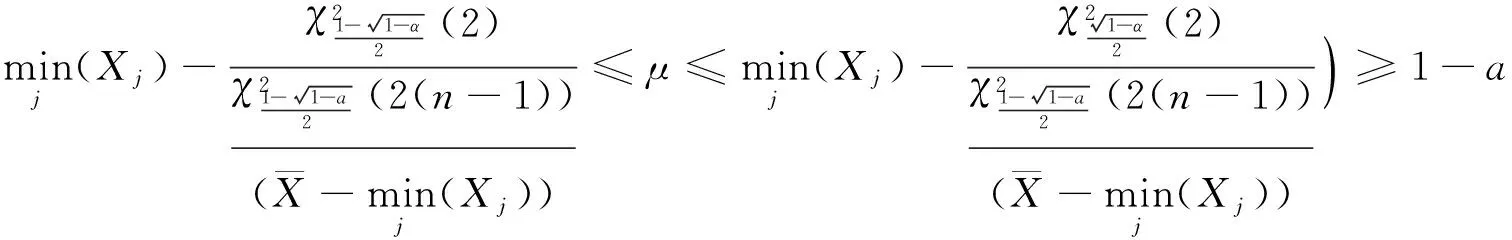
λ,μ的置信度为(1-α)%的联合置信区间为
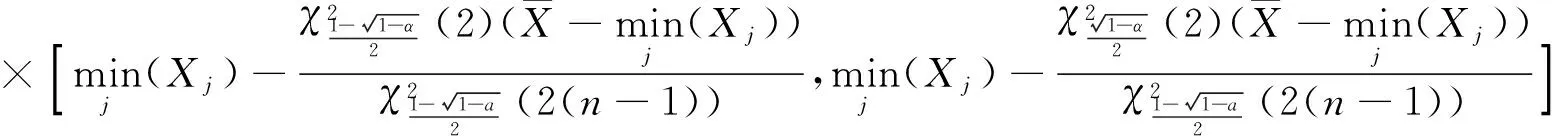

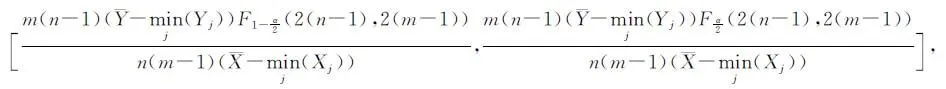
当λ1=λ2=λ,n=m时,μ1-μ2的置信度为(1-α)%的置信区间为
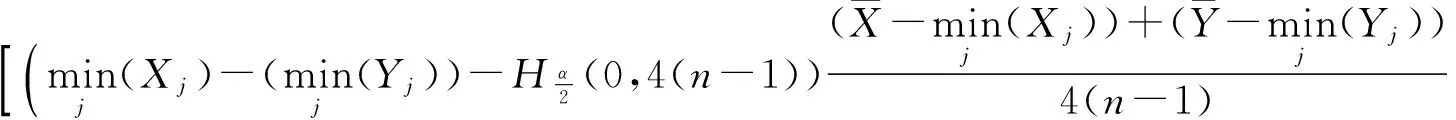
证 由指数分布抽样基本定理
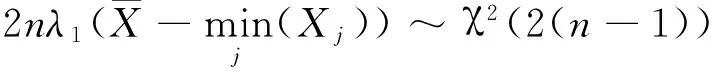
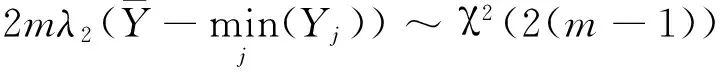
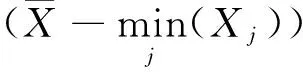

得
=1-α,


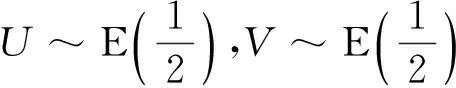
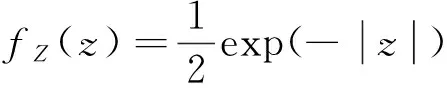
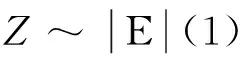
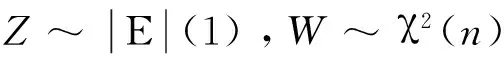
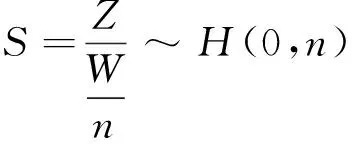
当λ1=λ2=λ,n=m时,由
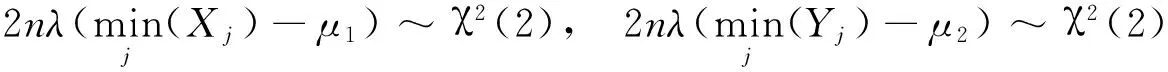
都相互独立,则
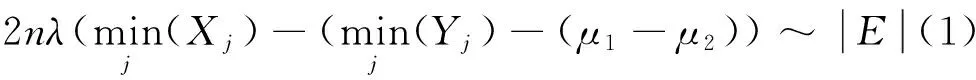
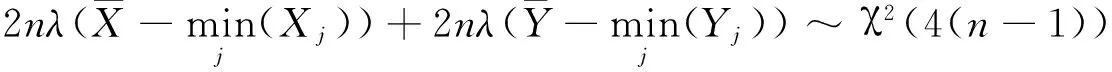
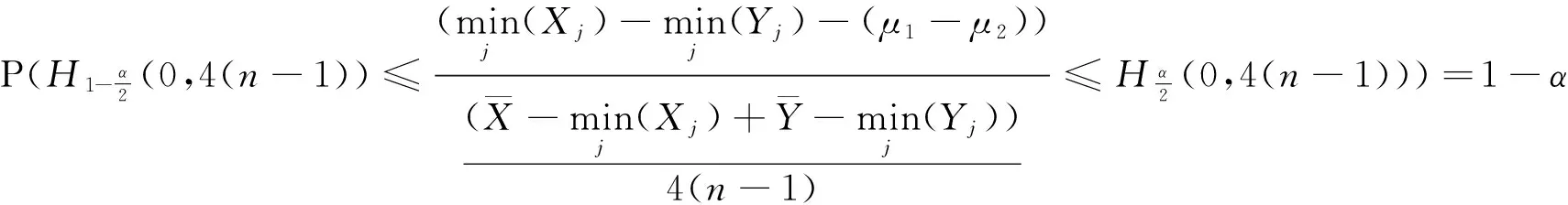
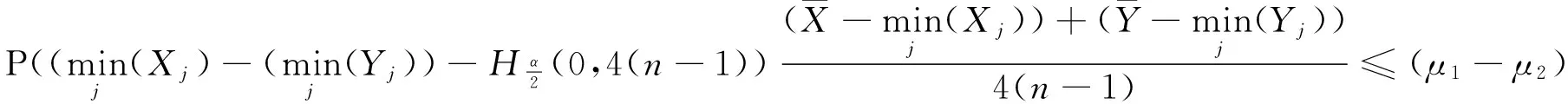

μ1-μ2的置信度为(1-α)%的置信区间为
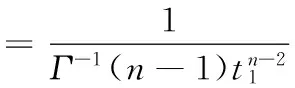
与λ,μ无关,得充分性;
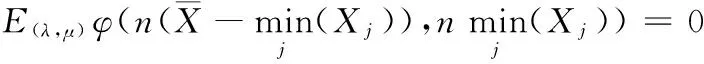

对μ求导得
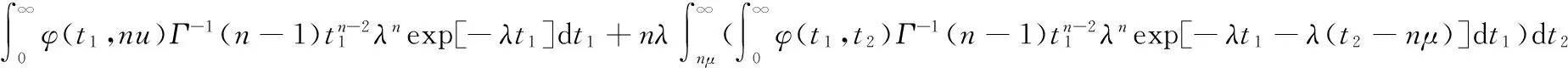
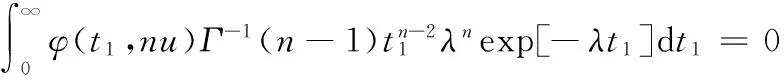
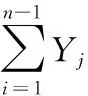
附录2 模拟分析:取λ=2,μ=3,α=0.05,得表1;取λ1=3,λ2=2,μ1=2,
μ2=5,α=0.05,得表2;取λ1=1,λ2=1,μ1=5,μ2=2,α=0.05,得表3.

表1 定理2、定理3、定理4的模拟结果

表2 定理5的模拟结果(n≠m)

表3 定理5的模拟结果(n=m)
[1] 郑明,陈子毅,汪嘉冈.数理统计讲义[M].上海:复旦大学出版社,2012.
[2] 陈家鼎,孙山泽,李东风,刘力平.数理统计学讲义[M].北京:高等教育出版社,2015.
[3] Li Juan,Song Weixing,Shi Jianhong.Parametric bootstrap simultaneous confidence intervals for differences of means from several two-parameter exponential distributions[J].Statistics and Probability Letters ,2015,106:39-45.
[4] Sun Xiaoqian,Zhou Xian,Wang Jinglong.Confidence intervals for the scale parameter of exponential distribution based on Type II doubly censored samples[J].Journal of Statistical Planning and Inference,2008,138:2045-2058.
[5] Hajebi M,Rezaei S,Nadarajah S.Confidence intervals for P(Y < X) for the generalized exponential distribution [J].Statistical Methodology,2012,9:445-455.
[6] Wang Liang,Shi Yimin.Reliability analysis of a class of exponential distribution under record values[J].Journal of Computational and Applied Mathematics,2013,239:367-379.
[7] Balakrishnan N,Xie Q H.Exact inference for a simple step-stress model with Type-II hybrid censored data from the exponential distribution[J].Journal of Statistical Planning and Inference,2007,137:2543-2563.
[8] Balakrishnan N,Xie Q H.Exact inference for a simple step-stress model with Type-I hybrid censored data from the exponential distribution[J].Journal of Statistical Planning and Inference,2007,137:3268-3290.
[9] Ganguly A ,Mitra S,Samanta D,Kundu D.Exact inference for the two-parameter exponential distribution under Type-II hybrid censoring[J].Journal of Statistical Planning and Inference,2012, 142:613-625.
[10] Cramer E,Balakrishnan N.On some exact distributional results based on Type-I progressively hybrid censored data from exponential distributions [J].Statistical Methodology,2013,10:128-150.
[11] 李国安.二元Freund型指数分布的特征及参数估计[J].大学数学,2012,27(5):48-51.
[12] 李卫华,李国安,王伟,李茂华.二元一般指数分布的识别性及其参数估计[J].大学数学,2016,32(2):81-85.
[13] Gorny J,Cramer E.Exact likelihood inference for exponential distributions under generalized progressive hybrid censoring schemes [J].Statistical Methodology,2016,29:70-94.
Sampling Fundamental Theorem for Exponential Distribution with Application to Parametric Inference of Exponential Distribution
LIGuo-an
(Department of Mathematics, Ningbo University, Ningbo, Zhejiang 315211, China)
This article discovers the sampling fundamental theorem for exponential distribution, and applies it into parametric inference of the two-parameter exponential distribution, uniformly minimum-variance unbiased estimator (UMVUE) of parameters of the exponential distribution are derived;and confidence intervals and joint confidence region of parameters for one population are obtained; also confidence intervals of ratio and minus of parameters for two population are obtained.
sampling fundamental theorem for exponential distribution; parametric inference; uniformly minimum variance unbiased estimator; confidence intervals; joint confidence region
2016-04-08; [修改日期]2016-05-31
宁波大学学科项目(XKL14D2037)
李国安(1964-),男,硕士,副教授,从事概率统计与土地估价研究.Email:liguoan@nbu.edu.cn
O212.1
A
1672-1454(2016)05-0030-07
