基于量测一步预测信息的自调整UKF

黄　平, 詹洋燕, 程广舟

(哈尔滨工程大学自动化学院, 黑龙江 哈尔滨 150001)



基于量测一步预测信息的自调整UKF

黄平, 詹洋燕, 程广舟

(哈尔滨工程大学自动化学院, 黑龙江 哈尔滨 150001)

摘要：针对无迹卡尔曼滤波(unscented Kalman filter, UKF)中自由调节参数的选取问题,通过研究不同的对于滤波性能的影响,提出基于量测一步预测信息的在线自调整的UKF方法。所提方法是通过根据每一滤波时刻量测的一步预测信息,对滤波参数进行选取,选出每一滤波时刻的最优滤波参数,从而实现算法的在线调整。数值仿真表明,基于量测一步预测信息的自调整UKF对于真实状态的跟踪效果要优于固定参数的无迹卡尔曼滤波。

关键词：自调整; 无迹卡尔曼滤波; 非线性; 一步预测信息

0引言

扩展卡尔曼滤波(extend Kalman filter,EKF)是工程上使用最早的非线性滤波方法[1]。自从20世纪60年代提出以来,被广泛应用到各个领域[2]。但是,面对强非线性系统时,由于存在高阶项的截断误差EKF，很可能会导致滤波的发散。基于“对概率分布进行近似要比对非线性函数近似容易很多”的观点，文献[3]提出了无迹卡尔曼滤波器(unscented Kalman filter,UKF)。

从UKF产生开始,在状态向量服从正态分布时,人们一直认为满足n+k=3(n为系统的维数)时,无损变换(unscented transformation,UT)能够有比较出色的表现[4-6]。随着容积卡尔曼滤波(cubature Kalman filter,CKF)的产生,使得调节参数κ的选取再次成为人们关注的焦点问题[7-8]。虽然UKF与CKF滤波有着不同的假定和理论推导,但是从滤波方法上来看,CKF滤波实质上就是UKF的一种特例(κ=0)。两种滤波在不同维数下的滤波精度是不同的,也就是说κ的选取并不是固定不变的。因此本文提出一种基于量测残差的自调整UKF,即根据量测信息对κ进行在线调节,提高滤波的精度。

1UKF

1.1UT变换

假设x∈Rn,y∈Rny是任意的随机量,且x和y具有的非线性映射关系为

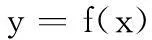
(1)

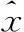
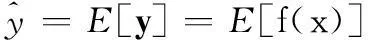
(2)

(3)

(4)

UT变换就是通过选取一系列具有相应权值的Sigma点{χi}来近似变量的统计特性。

采点方式和相应的权值[9-10]为

(5)

(6)

(7)

(8)

(9)

(10)

(11)

将UT变换应用到高斯滤波器上,便产生了UKF滤波[11]。

1.2UKF滤波的均值近似误差分析

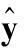
(12)

(13)

式中,A⊗B为矩阵A和B的克罗尼克积;A⊙n代表A的n次克罗尼克幂。同时,f(x)对向量x的k次导数定义为

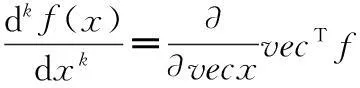
(14)

vec(A)定义为

(15)

式中,A是一个p×q的矩阵；ai是它的第i列。依据泰勒级数展开式,则UT变换误差的表达式为

(16)

为了清晰地表达数学变量,记

(17)

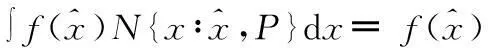
则可以得到误差的表达式为

(18)

根据对称性,各奇阶矩均为零。UT变换的误差可以表示为

(19)

按照式(5)～式(7)传统UKF滤波选取Sigma点的方式,UT变换能够精确地捕获到非线性函数的2阶矩信息,即

(20)

如果状态变量服从高斯正态分布,当κ=3-n时,UT变换不仅能够精确捕获系统的2阶矩,而且还能够捕获系统大部分的4阶矩信息[14]。但是,对于不同的非线性函数f(x),由于非线性度不同,可能会导致在进行泰勒级数展开时一些高阶矩信息对UT变换的影响会大于大部分的4阶矩信息,特别是系统模型非线性度比较强时影响更加明显。这样,有可能一些高阶矩信息对于变换后统计均值和方差的求取是十分有利的。而且,传统上调节参数的选取只考虑到状态变量的先验概率密度,并没有考虑到量测信息及系统模型的影响。因此,在单次滤波之前考虑量测量的一步预测信息确定出自由调节参数κ的值是十分必要的。

2在线调整算法

一般可以适当选取κ值去逼近量测量一步预测的先验概率密度,但是量测量的先验概率密度一般是无法精确得到的[15]。而量测的一步预测信息分布越集中，说明一步预测越是准确的。因此,可以根据一步预测中量测量的各阶距来保证对量测预测值的逼近。一般情况,需要保证量测信息的离散度(方差)越小即能够表征预测信息的准确性。

(21)

由于量测的一步预测概率密度无法精确获取,这里根据量测的一步预测的二阶矩信息保证逼近真实概率密度。其中K是调节参数κ的取值范围,即

是一些固定性的可能取值且满足误差的协方差阵正定。滤波算法步骤具体如下:

步骤 1根据具体非线性模型,选取κ′的值；

令k=k+1,算法继续从步骤3进行。

这样,整个自调整算法既保证了UT变换中系统捕获均值的精确性,又保证了充分利用到量测的一步预测信息。可以看出,相比传统的固定参数的UKF滤波,自调整UKF中加入了步骤3。这样,滤波的精度相比固定参数的UKF滤波将会整体得到提高,而且,系统模型的非线性越强效果越会明显。但是,这是以牺牲计算量为前提的,而且调节参数的取值范围越大、步长step越小,那么计算量就会越大、算法的运行时间就会越长。

3算法仿真

选取强非线性高斯系统数学模型,用以验证自调整UKF的有效性。离散方程[16]为

式中,k=1,2,…,P；ΔT=0.01,过程噪声和量测噪声为互不相关的零均值高斯白噪声,其统计特性分别为wk～N(0,0.09),vk+1～N(0,0.5)。状态初始真实值x0=2.3,仿真初始条件取x0|0=2.3,P0|0=0.01,总仿真步数P=100,仿真次数M=50。自调整的UKF和固定参数UKF两种滤波器的估计性能采用定义的时间平均MSE进行比较。

式中,xk为理论值;xk|k为滤波估计值;P为总仿真步数;M为仿真次数。通过仿真,表1首先给出了几组不同调节参数下的MSE值。可以看到,当调节参数取1的时候对应有最小的MSE值。文献[1]明确给出了结果,即对于一维和二维非线性系统UKF的滤波精度要优于CKF(κ=0)的滤波精度。但是不难看到,κ=2对应的MSE并不是最优的。因此,无论是κ=0还是κ=2都难以达到最优的滤波效果。

表1　不同κ对应的MSE值

表2给出了调节参数的几个典型的固定值和两组自调整值下的MSE及各自的算法实际物理运行时间。

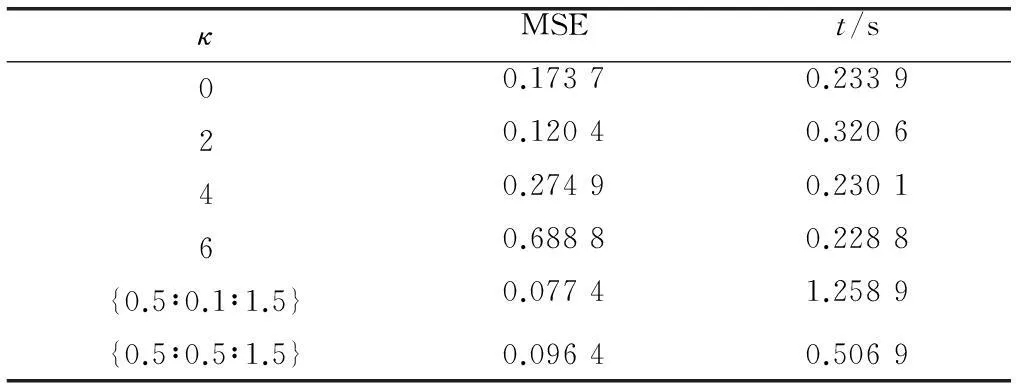
表2　κ在不同条件下的MSE及算法运行时间

不难看出,自调整UKF的MSE均小于固定参数的UKF。而且在调节参数的范围相同时,步长越小,MSE就越小,滤波的精度也越高。但是,自调整UKF算法的运行时间却提高了。因此,自调整UKF的关键就是根据实际的需要适当选取调节参数的步长,协调好精度与算法运行时间的关系。

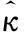
图1　固定参数UKF和自调节UKF跟踪效果

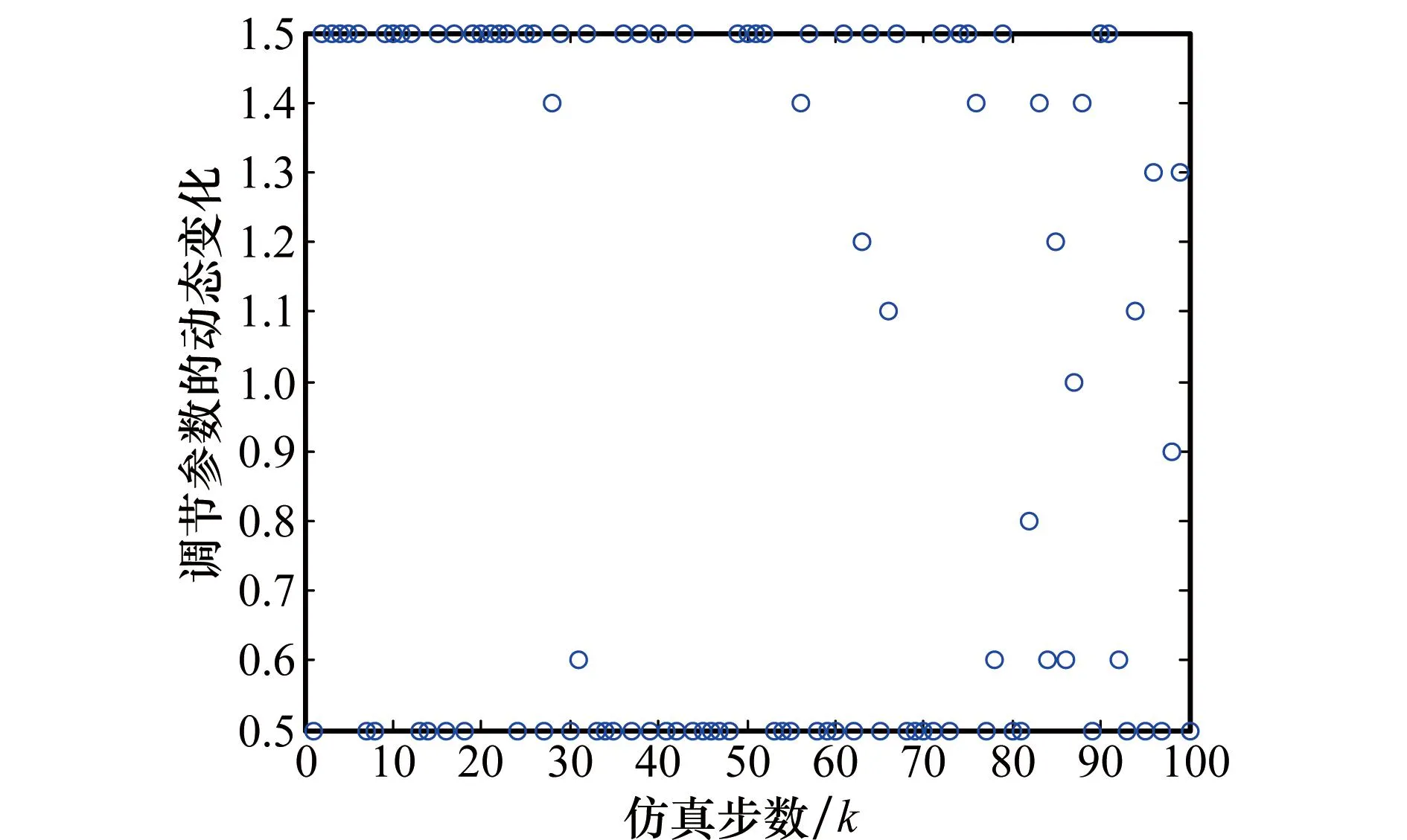
图k的动态变化

4结论

针对UKF滤波中自由调节参数的选取问题,进行了理论分析和仿真验证,并在此基础之上提出了基于量测信息的自调整UKF滤波方法。为满足精度的需求,在实际应用中κ′的选择可以遵循以下规则:当维数n≤3时,令κ′=3-n;当n>3时,令κ′=0。而本方法的核心在于在每一次滤波之前都要先根据量测的一步预测信息确定调节参数的值,然后在最优值下进行状态均值和协方差的求取。从仿真结果看,在整个滤波过程中自调整UKF滤波比传统固定参数的UKF滤波跟踪精度要高,能够比较精确地跟踪真实状态。但是,在实际中不能一味增加调节参数的取值范围、减小步长(通常可以选择step=0.5即可满足精度的要求)。否则计算量会急剧增加、算法运行时间时间也会明显变长,但是精度的提高却不是很明显。因此,一定要根据具体的需要适当选取调节参数的范围与调节步长。

参考文献：

[1] Athans M, Wishner R P, Bertolini A. Suboptimal state estimation for continuous time nonlinear systems from discrete noisy measurements[J].IEEETrans.onAutomaticControl,1968,13(5):504-514.

[2] Kailath T. A review of three decades of linear filtering theory[J].IEEETrans.onAutomaticControl, 1974, 20(2): 146-181.

[3] Anastasia D, Andreopoulos Y. Throughput-distortion computation of generic matrix multiplication: toward a computation channel for digital signal processing systems[J].IEEETrans.onSignalProcessing, 2012, 60(4): 2024-2037.

[4] Ienkaran A, Simon H. Cubature Kalman filters[J].IEEETrans.onAutomaticControl, 2009,54(6): 1254-1269.

[5] Julier S J, Uhlman J K, Durrant-Whyte H F. A new method for the nonlinear transformation of means and covariances in filters and estimators[J].IEEETrans.onAutomaticControl,2000,45(3):477-482.

[6] Jia B, Xin M, Cheng Y. High-degree cubature Kalman filter[J].Automatica,2013, 49(2): 510-518.

[7] Mohammad T S, Pouria S, Mostafa Z. Extended and unscented Kalman filters for parameter estimation of an autonomous underwater vehicle[J].OceanEngineering, 2014, 91(15): 329-339.

[8] Kokiopoulou E, Frossard P. Polynomial filtering for fast convergence in distributed consensus[J].IEEETrans.onSignalProcessing, 2009, 57(1): 342-354.

[9] Jinwhan K, Vaddi S S, Menon P K, et al. Comparison between nonlinear filtering techniques for spiraling ballistic missile state estimation[J].IEEETrans.onAerospaceandElectronicSystems, 2012, 48(1): 313-328.

[10] Bisht S S, Singh M P. An adaptive unscented Kalman filter for tracking sudden stiffness changes[J].MechanicalSystemsandSignalProcessing, 2014,49(1/2):181-195.

[11] Zhang H T, Dai G, Sun J S, et al.Unscented Kalman filter and its nonlinear application for tracking a moving target[J].Optik-InternationalJournalforLightandElectronOptics, 2013,124 (20): 4468-4471.

[12] Li W L, Jia Y M.Consensus-based distrbuted multiple model UKF for jump Markov nonlinear systems[J].IEEETrans.onAutomaticControl, 2012,57(1): 230-236.

[13] Jindich D, Miroslav, Ondej S. Unscented Kalman filter:aspects and adaptive setting of scaling parameter[J].IEEETrans.onAutomaticControl, 2012,57(9): 2411-2416.

[14] Terra M, Ishihara J, Jesus A. Information fitering and array algorithms for discrete-time Markovian jump linear systems[J].IEEETrans.onAutomaticControl, 2009,54(1): 158-162.

[15] Aysal T, Oreshkin B, Coates M. Accelerated distributed ave-rage consensus via localized node state prediction[J].IEEETrans.onSignalProcessing, 2009, 57(4): 1563-1576.

[16] Duník J, Simandl M, Straka O. Adaptive choice of scaling parameter in derivative-free local filters[C]∥Proc.oftheIEEEConferenceonInformationFusion, 2010: 1-8.

黄平(1980-)，男,讲师,博士,主要研究方向为惯性导航技术。

E-mail: hppmonkeyking@163.com

詹洋燕(1991-)，女,硕士研究生,主要研究方向为非线性滤波理论。

E-mail: guiruixiao@sina.com

程广舟(1988-)，男,硕士研究生,主要研究方向为非线性滤波理论。

E-mail: guangzhoucheng123@163.com

Adaptive setting of scaling parameter of UKF based on step prediction information of measurement

HUANG Ping, ZHAN Yang-yan, CHENG Guang-zhou

(CollegeofAutomation,HarbinEngineeringUniversity,Harbin150001,China)

Abstract:For the adjustable parameter selection problem of κ in the unscented Kalman filter(UKF), through the study of the impact of the different κ for filtering, the method based on the step prediction information of the measurement, which is an online adjustment of the UKF, is presented. Based on the prediction information of measurement in every filtering time, the filtering parameter is selected, which is optimal and can realize the on-line adjustment. Numerical simulations show that the adjustment UKF based on the step prediction information of the measurement tracks the real state better than the traditional UKF.

Keywords:adaptive setting; unscented Kalman filter (UKF); nonlinear; step prediction information

收稿日期：2014-12-16；修回日期：2015-05-18；网络优先出版日期：2015-08-31。

基金项目：国家自然科学基金(61403091)；中国博士后科学基金(2014T70310)资助课题

中图分类号：TP 391

文献标志码：A

DOI:10.3969/j.issn.1001-506X.2016.06.27

作者简介：

网络优先出版地址：http:∥www.cnki.net/kcms/detail/11.2422.TN.20150831.1932.014.html