EM算法对不完全数据下指数分布的参数估计

张梦琇

石河子大学理学院 新疆石河子 832000

1 概述

数据的收集是处理统计问题的关键，由于测量精度不高，调查者在收集处理数据时经常会出现测量不精准的情况，调查者收集到的数据大多是缺失数据，对于缺失数据而言，调查者经常或遇到这样两类数据，一类数据是指在设定的时间间隔之前，研究对象就已经结束工作，这种数据称之为删失数据；另一类数据是指在设定的时间间隔之后，该研究对象仍持续地进行这种操作，此种数据被称之为截断数据。研究生活中的自然现象需要数据的支撑，采用最多的数据类型为左截断右删失数据，本文以左截断右删失数据为基础数据类出，主要处理不完全信息数据，它包括截断数据、删失数据以及既截断又删失数据。本文以带有不完全信息下的数据作为研究对象，结合特定的分布，探究不完全信息数据下指数分布的参数估计问题。

指数分布是一种常用的连续型寿命函数，被广泛应用于检测电子元件的使用寿命。文献[1-3]探究了带有缺失数据下指数分布的参数估计，这三篇文章从不同的数据类型，不同参数下的指数分布研究指数分布的参数估计；文献[4-6]研究了左截断右删失下不同分布多变点模型的Bayes估计，这三篇文章主要研究指数分布的贝叶斯估计；文献[7]主要研究了带有不完全信息的不同分布下的变点模型，作者主要研究其他分布下的不完全数据的参数估计问题；文献[8]利用EM算法研究了指数分布的参数估计，作者研究完全数据下的指数分布。本篇文章将EM算法与不完全数据结合到一起，考察指数分布参数变点在数据不完整的情况下的迭代表达式。首先，利用EM算法对不完全信息下的指数分布的参数进行了研究与分析，随后，利用R软件进行数值模拟，检验不完全信息下的指数分布参数的迭代式的精确性。最后，随机模拟的结果表明，迭代式的精度较高，并且提高了计算速度。

2 连续型寿命IIRCT(带有不完全信息随机截尾试验Random censoring test with incomplete information，简称IIRCT)

假设产品寿命X1，X2，…是相互独立同分布的连续型随机变量序列，其分布函数为F(x；λ)=P(Xi≤x)，概率密度函数为f(x；λ)，其中，λ为未知参数。又设Y1，Y2，…是相互独立的、取值为非负整数的连续型随机变量序列，分布函数分别为G1(y)，G2(y)，…，概率密度函数为g1(y)，g2(y)，…，且gi(y)与未知参数λ无关。假定随机变量序列{Xi}与{Yi}是相互独立的。

为了估计连续型随机序列的未知参数λ，选取样本容量为n的样本作为观测数集，则这n个样本的观测数据记为{Zi，1≤i≤n}如下：

(1)当Xi≤Yi时，分为以下两种情况：①Xi以概率ai立即显示，此时，记为Zi=Xi；②Xi以概率1-ai不被显示，此时，记为Zi=Yi，其中，ai称为失效显示概率，即：

(2)当Xi>Yi时，取Zi=min(Xi，Yi)，即Zi=Yi。

为了研究方便，本文引入如下的示性变量αi，βi，i=1，2，…，n。

若Xi≤Yi成立，则αi=1；否则，当Xi>Yi成立，则αi=0；

若Xi≤Yi并且Xi未被显示，βi=0；其他情况，βi=1。

假定，前n1个样本数据满足Xi≤Yi(i=1，2，…，n1)，剩余n2个样本数据满足Xi>Yi成立，所以，该似然函数为：

下面对于满足αi=1，βi=0的缺失观测数据，进行增添数据，对增添后的新数据重新建立似然函数，若第i个样本的寿命值没有被显示，(i=1，2，…n1)，添加的观测值为(ti，γi，ωi)，其中ti=xi∧yi=min(xi，yi)，γi=I(xi≤yi)，i=1，2，…n1；示性变量ωi表示，若满足Xi≤Yi，并且Xi未被显示ωi=0；其他情况，ωi=1，i=1，2，…n1。添加缺损数据后，所得到的似然函数为：

其中:

3 IIRCT下指数分布的参数估计

若X服从参数为λ的指数分布，指数分布的似然函数为：

(1)

利用统计思想，建立似然函数，对不完全数据进行统计分布。对于不完全信息下的指数分布的数据而言，似然函数的概率密度核的形式只与未知参数有关，则(1)表示不完全信息下的指数分布的似然函数的概率密度核的形式。

由于αi，βi表示当i=1，2，…，n的示性变量，所以，当i=1，2，…，n1时，有αi=γi，βi=ωi。

(2)

将(2)式代入(1)式，替换掉(1)中的γi和ωi，i=1，2，…，n1。

所以:

假设λ(i)为第i步的初始迭代值，利用EM算法，根据带有不完全信息的指数分布的迭代式计算，每次迭代可得到一个新的估计值λ(i+1)。

下面我们采用EM算法对不完全信息下的指数分布数据进行优化处理：

EM算法是一种迭代优化策略，由于它的计算方法中每一次迭代都分两步，其中一个为期望步(E步)，另一个为极大步(M步)，所以算法被称为EM算法(Expectation-Maximization Algorithm)，最初是为了解决数据缺失情况下(包含隐变量)的参数估计问题。

其基本思想是：首先根据已经给出的观测数据，估计出模型参数的值(初始化)；然后再依据上一步估计出的参数值估计缺失数据的值，再根据估计出的缺失数据加上之前已经观测到的数据重新再对参数值进行估计，然后反复迭代，直至最后收敛，迭代结束。

操作步骤具体如下：

(1)E步：

接下来，计算Ti的密度函数：

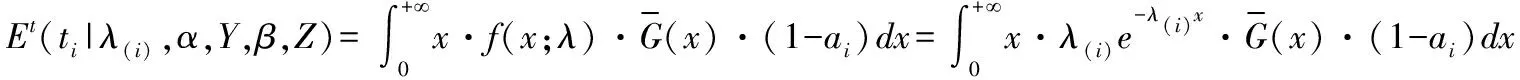
(2)M步：

(3)若带有不完全信息的数据也服从指数分布，即G～E(λ1)，那么，有：

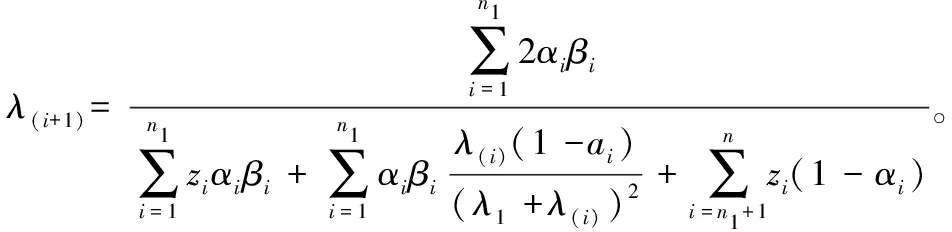
(3)

通过假设数据服从的分布类型，利用EM算法建立不完全数据下指数分布的参数估计的迭代公式，如(3)式所示。

4 数值模拟

为了检验不完全数据下指数分布的参数估计的迭代公式的收敛速度和收敛精度，利用R软件进行数值模拟。分别从不完全数据所服从指数分布的参数相同和参数不同的两个角度进行考虑。从而验证不完全数据下指数分布的参数估计的迭代公式的收敛速度和收敛精度。

4.1 不同参数下的指数分布

利用R软件，结合EM算法，对指数分布的未知参数λ，进行统计推断，我们主要进行五组试验，假定不完全信息的分布是参数λ1=2恒定不变，每组都进行n=100的随机模拟试验，具体情况如下表所示：

表1 n=100，λ1=2时，参数λ的模拟结果

通过上表，我们能发现利用EM算法，对指数分布进行数值模拟，参数λ的精度较高，误差限在10-4，即误差较小，迭代次数在27～45之间。因此，采用EM算法对未知参数进行检验是可取的。

4.2 不同参数下的不完全信息

利用R软件，结合EM算法，对指数分布的未知参数λ，进行统计推断，我们主要进行五组试验，假定缺损数据的分布是参数λ(i)=2恒定，每组进行n=100的随机模拟试验，具体情况如下表所示：

表2 n=100，λ(i)=2时，参数λ的模拟结果

通过上表，可以看出，不完全信息的分布下的指数分布的参数收敛较快，但精度不高，精度为10-2。利用不完全信息下的指数分布的迭代公式的次数减少了，迭代速度较相同参数的不完全信息下的指数分布的情况下减少了迭代时间，加快了迭代速度。

总之，对于不完全信息下的指数分布参数的迭代式，收敛速度快，精度较高，利用EM算法处理不完全信息下的指数分布是可取的。