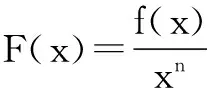联想求导法则 构造函数解题——由2015年两道高考题想到的

敖德兵

(四川省成都市北京师范大学成都实验中学，610017)



联想求导法则构造函数解题
——由2015年两道高考题想到的

敖德兵

(四川省成都市北京师范大学成都实验中学，610017)

联想是由当前感知或思考的事物想起有关的另一事物,或者由头脑中想起的一件事物,又引起想到另一件事物.由于客观事物是相互联系的,各种知识也是相互联系的,因而在思维中,联想是一种基本的思维形式.因此,在解题过程中,要善于观察题设条件与所求结论的结构特征,分析题设与结论之间的联系,联想题目与已有知识结构的相似性.本文结合导数运算法则,举例说明之.

一、联想函数和、差的求导法则构造函数

例1(2015年福建高考题)若定义在R上的函数f(x)满足f(0)=-1,其导函数f ′(x)满足f ′(x)>k>1,则下列结论中一定错误的是()

分析联系条件与结论之间的结构特征的关系,可利用和、差函数的求导法则构造函数,从而达到求解的目的.

解由已知，导函数f ′(x)满足f ′(x)>k>1,构造函数

g(x)=f(x)-kx,

则 g′(x)=f ′(x)-k>0,

所以g(x)在R上单调递增,且

g(0)=f(0)-k·0=-1.

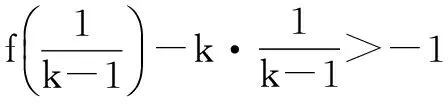
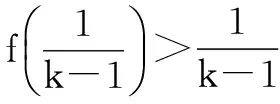
所以选项C一定错.故选C.

变式1(2011年辽宁高考题)函数f(x)的定义域为R,f(-1)=2,对任意x∈R,f ′(x)>2,则f(x)>2x+4的解集为 ()

(A) (-1,1)(B) (-1,+∞)

(C) (-∞,-1)(D) (-∞,+∞)

解导函数f ′(x)的正负决定着函数的单调性,由f ′(x)>2联系到结论中的f(x)>2x+4,则问题豁然开朗.构造函数g(x)=f(x)-2x-4,则f(x)>2x+4等价于g(x)>0.由f ′(x)>2，得g′(x)=f ′(x)-2>0,即函数g(x)在(-∞,+∞)单调递增,又f(-1)=2,所以g(-1)=f(-1)+2-4=0.综上，f(x)>2x+4等价于g(x)>g(-1),所以x>-1.故选B.

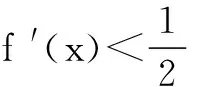
(A) (-1,1)

(B)(-∞,-1)

(C) (-∞,-1)∪(1,+∞)

(D) (1,+∞)

解构造F(x)=2f(x)-x-1,则F′(x)=2f ′(x)-1<0,所以F(x)为R上的减函数.又因为F(1)=2f(1)-1-1=0,2f(x)1,选D.

二、联想积函数的求导法则构造函数

例2(2004年湖南高考题)设函数f(x)，g(x)分别是定义在R上的奇函数和偶函数,当x<0时,f ′(x)g(x)+f(x)g′(x)>0,且g(3)=0,则不等式f(x)g(x)<0的解集为()

(A) (-3,0)∪(3,+∞)

(B) (-3,0)∪(0,3)

(C) (-∞,-3)∪(3,+∞)

(D) (-∞,-3)∪(0,3)

解由f ′(x)g(x)+f(x)g′(x)>0联想到[f(x)g(x)]′=f ′(x)g(x)+f(x)g′(x)>0,所以F(x)=f(x)g(x)在(-∞,0)上为增函数.又f(x)，g(x)分别是定义在R上的奇函数和偶函数,所以F(x)=f(x)g(x)为奇函数,从而F(x)=f(x)g(x)在(0,+∞)为增函数.而由F(3)=f(3)，g(3)=0得F(-3)=f(-3)g(-3)=0,结合函数图象可得f(x)g(x)<0的解集为(-∞,-3)∪(0,3)，选D.

评注本题由f ′(x)g(x)+f(x)g′(x)>0联想积的求导法则,构造F(x)=f(x)g(x),特别地,

(1)若xf ′(x)+nf(x)>0(或<0),可构造F(x)=xnf(x)；

(2)若f ′(x)+f(x)>0(或<0),可构造F(x)=exf(x).

变式1(2009年天津高考题) 设函数f(x)在R上的导函数为f ′(x),且2f(x)+xf ′(x)>x2,下面的不等式在R上恒成立的是 ()

(A) f(x)>0(B) f(x)<0

(C) f(x)>x(D) f(x)

解构造F(x)=x2f(x),则F′(x)=x[2f(x)+xf ′(x)].当x>0时,F′(x)=x[2f(x)+xf ′(x)]>x3>0,所以F(x)在(0,+∞)递增,得F(x)>F(0)=0,即x2f(x)>0,故f(x)>0.

同理可得当x<0时,F′(x)<0,F(x)在(-∞,0)递减,所以F(x)>F(0)=0,即x2f(x)>0,故f(x)>0.综上可知选A.

变式2设函数f(x)的定义域为R,且对任意x∈R,f ′(x)+f(x)>0,则对任意正数a,必有()

(A)f(a)>eaf(0)(B) f(a)

变式3(2007年陕西高考题)f(x)是定义在(0,+∞)上的非负可导函数,且满足xf ′(x)+f(x)≤0.对任意正数a、b,若a

(A)af(b)≤bf(a)(B)bf(a)≤af(b)

(C)af(a)≤f(b)(D)bf(b)≤f(a)

解构造函数g(x)=xf(x),则g′(x)=xf ′(x)+f(x)≤0,所以g(x)在(0,+∞)内是单调减函数或是常数函数.又0

f(b)≤f(a),又a

(A)有极大值,无极小值

(B)有极小值,无极大值

(C)既有极大值又有极小值

(D)既无极大值也无极小值

令φ(x)=ex-2F(x),则

φ′(x)=ex-2F′(x)

∴φ(x)在(0,2)内单调递减,在(2,+∞)内单调递增,

∴φ(x)的最小值为φ(2)=e2-2F(2)=0，∴φ(x)≥0.

又x>0,∴f ′(x)≥0，

∴f(x)在(0,+∞)单调递增，

∴f(x)既无极大值也无极小值，故选D.

三、利用函数商的求导法则构造函数

例3(2015年全国高考题)设f ′(x)是奇函数f(x)(x∈R)的导函数,f(-1)=0,当x>0时，xf ′(x)-f(x)<0,则使f(x)>0成立的x的取值范围是()

(A)(-∞,-1)∪(0,1)

(B)(-1,0)∪(1,+∞)

(C)(-∞,-1)∪(-1,0)

(D)(0,1)∪(1,+∞)

评注作为商的求导法则的特例，我们有：

综上可见，联想求导法则,结合问题的外形结构特征与导数的形式特征进行合理构造函数是解决这类问题的关键.