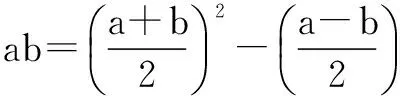极化恒等式的妙用

张城兵

(浙江省兰溪市第一中学，321102)



极化恒等式的妙用

张城兵

(浙江省兰溪市第一中学，321102)

众所周知,为求向量数量积最值或范围，一般有定义法、基底法、坐标法、几何意义法.下面例题均选自我省2015届高三模拟试题,难度中等偏上,这些题目用上述方法固然可

行,但从解答情况看较为繁琐.本文举例说明极化恒等式的应用,供读者参考.

一、两向量共同的起点为动点

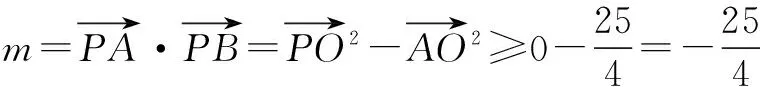
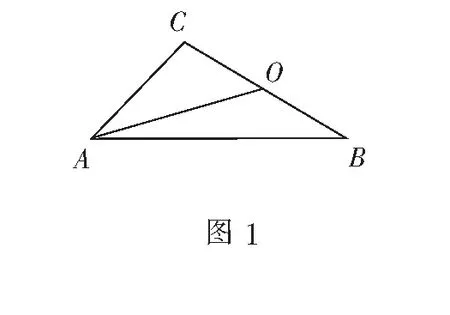
评注从解答过程看,并没有用条件“BC=3,AC=4”,可见它是多余的,命题者给出这多余的条件是想用坐标法,并要分别讨论点A在三边时的情况.

二、两向量终点均为动点

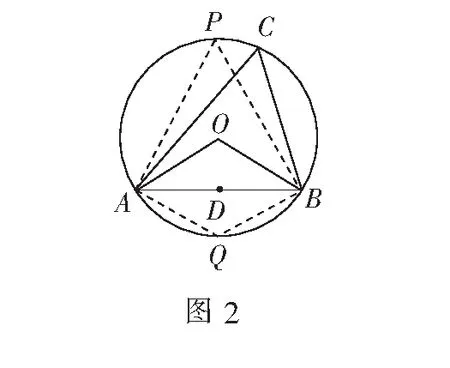
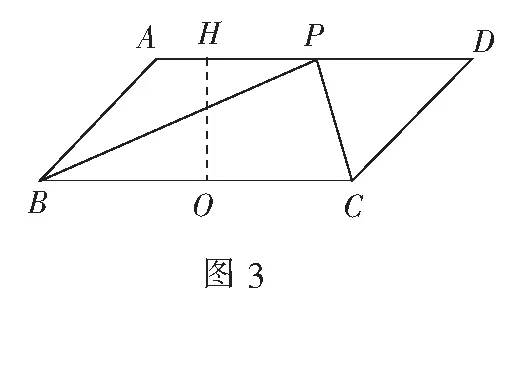
解取BC的中点N,连结AN，取其中点D,如图4,则

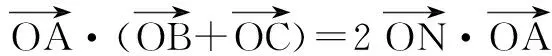
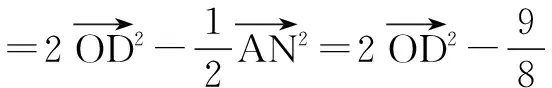
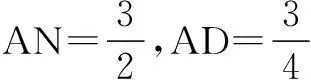
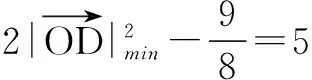
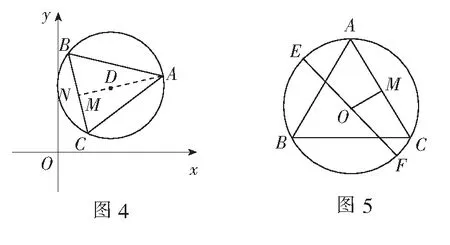
三、两向量的起点和终点均为动点

解由已知易求得外接圆半径为2.因为圆心O是EF的中点,所以

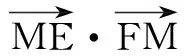
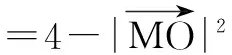
综观上述例题解法,因为两向量都是动态的,不是用极化恒等式能一劳永逸的,但它最大作用是化“多元变量”为“一元变量”,再加上必要时要构造图形,借助形的直观,发现最值何时取到就轻松解决问题.