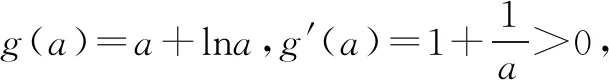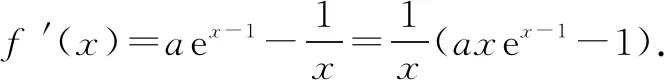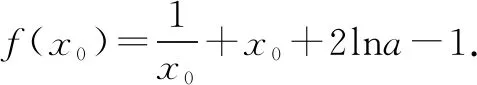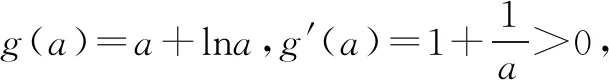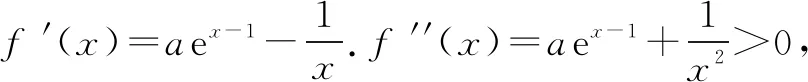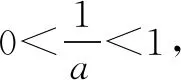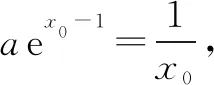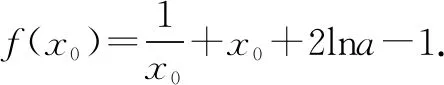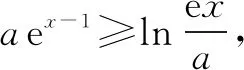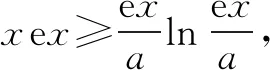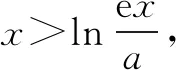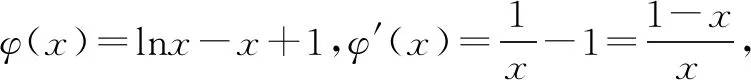多角度求解山东省高考21题

苏凡文

(山东省泰安宁阳一中 271400)

(山东省高考21)已知函数f(x)=aex-1-lnx+lna.

(1)当a=e时，求曲线y=f(x)在点(1,f(1))处的切线与两坐标轴围成的三角形的面积；

(2)若f(x)≥1，求a的取值范围.

解析(2)方法一：变换主元

由题意可得a>0.

①a≥1时，g(a)=aex-1-lnx+lna，因为ex-1>0，lna≥0，所以g(a)≥ex-1-lnx.易证ex-1≥x，所以ex-1-lnx≥x-lnx，易证得x-lnx≥1.所以f(x)≥1.

综上可得a≥1.

方法二：放缩法

由题意可得a>0.

易证明ex-1≥x成立，所以f(x)≥ax-lnx+lna.

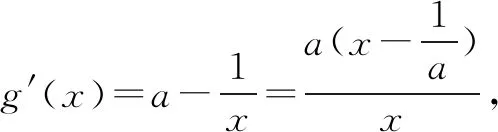
0

综上可得a≥1.

方法三：必要性开路(一)

其中，W为生产线平衡率，ti为第i工序循环时间，si为第i工位定员数，t0为流水线线节拍TT，a为流水线定员数。经计算得出，生产线平衡率W=52%，说明该生产线平衡率需要进行极大地改善。

由题意可得a>0.

综上可得a≥1.

必要性开路(二)

a=1时，f(x)=ex-1-lnx，易证ex-1≥x，所以f(x)≥x-lnx，易证x-lnx≥1，所以f(x)≥1成立.

综上可得a≥1.

方法四：同构函数